Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения части
Введем определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.
Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными (сила трения). Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю. Действительно, любой замкнутый путь (рис. 5.5) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле
 |
| Рис. 5.5. Работа в потенциальном поле сил |
потенциально, то, по условию 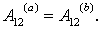 С другой стороны, очевидно, что
С другой стороны, очевидно, что 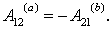 Поэтому
Поэтому
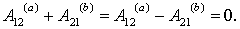
что и требовалось доказать.
Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 5.5). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. 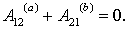 Отсюда
Отсюда 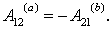 Но
Но 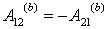 , поэтому
, поэтому 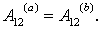
Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.
Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.
Обозначив эту функцию  , запишем
, запишем
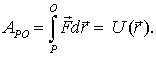 | (5.9) |
Функцию  называют потенциальной энергией частицы в данном поле.
называют потенциальной энергией частицы в данном поле.
Определим связь потенциальной энергии и силы поля. Взаимодействие частицы с окружающими телами можно описывать двумя способами: с помощью сил или с помощью потенциальной энергии. Наша задача - установить связь между потенциальной энергией и силой поля, точнее, определить поле сил 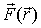 по заданной потенциальной энергии
по заданной потенциальной энергии  как функции положения частицы в поле.
как функции положения частицы в поле.
Ранее было показано, что при перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. 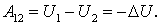 Это относится и к элементарному перемещению
Это относится и к элементарному перемещению 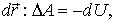 или
или
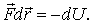 | (5.14) |
Учитывая, что 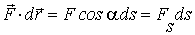 , где
, где 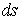 - элементарный путь, перепишем уравнение (5.14) в форме
- элементарный путь, перепишем уравнение (5.14) в форме

где 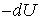 - это убыль потенциальной энергии в направлении перемещения
- это убыль потенциальной энергии в направлении перемещения 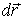 . Отсюда
. Отсюда
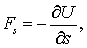 | (5.15) |
т. е. проекция силы поля - вектора 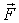 - в данной точке на направление перемещения
- в данной точке на направление перемещения 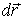 равна с обратным знаком производной потенциальной энергии
равна с обратным знаком производной потенциальной энергии 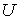 по данному направлению. Символ
по данному направлению. Символ  - частной производной - подчеркивает, что производная берется по определенному направлению.
- частной производной - подчеркивает, что производная берется по определенному направлению.
Перемещение 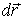 мы можем взять в любом направлении, в частности вдоль координатных осей х, у, z. Если перемещение
мы можем взять в любом направлении, в частности вдоль координатных осей х, у, z. Если перемещение 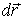 , например, параллельно оси х, то его можно представить так:
, например, параллельно оси х, то его можно представить так: 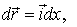 где
где 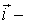 орт оси
орт оси 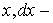 приращение координаты. x. Тогда paбота силы
приращение координаты. x. Тогда paбота силы 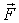 на перемещении
на перемещении 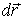 , параллельном оси x,
, параллельном оси x,

где 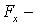 проекция вектора
проекция вектора 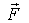 на орт
на орт 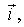 а не на перемещение
а не на перемещение 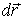 , как в случае
, как в случае 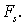
Подставив последнее выражение в уравнение (5.14), получим
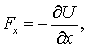
где символ частной производной означает, что потенциальная энергия 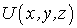 при дифференцировании должна рассматриваться как функция одного аргумента х, остальные же аргументы должны оставаться при этом постоянными. Ясно, что для проекций
при дифференцировании должна рассматриваться как функция одного аргумента х, остальные же аргументы должны оставаться при этом постоянными. Ясно, что для проекций 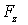 и
и 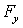 уравнения будут аналогичны уравнению для
уравнения будут аналогичны уравнению для 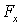 .
.
Итак, взяв с обратными знаками частные производные функции U по х, у и z, мы найдем проекции 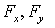 и
и 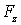 вектора
вектора 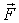 на орты
на орты  . Отсюда легко найти и сам вектор:
. Отсюда легко найти и сам вектор: 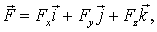 или
или
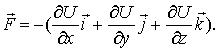
Величину, стоящую в скобках, называют градиентом (полным дифференциалом) скалярной функции U и обозначают 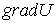 или
или 
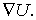 Мы будем пользоваться вторым, более удобным, обозначением, где значок
Мы будем пользоваться вторым, более удобным, обозначением, где значок 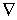 "набла" означает символический векторный оператор
"набла" означает символический векторный оператор
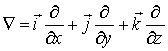 .
.
Т.о., сила, действующая на точку со стороны силового поля, выража-
ется через градиент потенциальной энергии точки в этом поле, взятый
с обратным знаком. Т.е. сила оказывается направленной в сторону наи-
быстрейшего убывания потенциальной энергии.
7.Нормировка потенциальной энергии.
Потенциальная энергия принимается равной нулю для некоторой конфигурации (координат) тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.  В этом случае говорят, что энергия нормирована на значение А 0 в поверхности земли.
В этом случае говорят, что энергия нормирована на значение А 0 в поверхности земли.
1. Мощность силы.
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
| ||
|
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
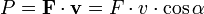 |
F — сила, v — скорость, α — угол между вектором скорости и силы.
Частный случай мощности при вращательном движении:
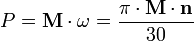 |
M — момент силы, 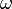 — угловая скорость, — число пи, n — частота вращения (число оборотов в минуту, об/мин).
— угловая скорость, — число пи, n — частота вращения (число оборотов в минуту, об/мин).
2. Энергия системы материальных точек.
Кинетическая энергия системы.
Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы
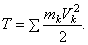
Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
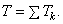
Кинетическая энергия – скалярная и всегда положительная величина.
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки 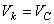
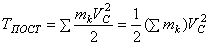 или
или 
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
2. Вращательное движение. Если тело вращается вокруг какой-нибудь оси Оz (см. рис.46), то скорость любой его точки 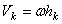 , где
, где 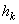 - расстояние точки от оси вращения, а w- угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:
- расстояние точки от оси вращения, а w- угловая скорость тела. Подставляя это значение и вынося общие множители за скобку, получим:
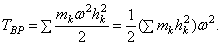
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:
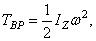
т. е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
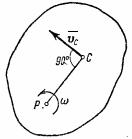
Рис.46
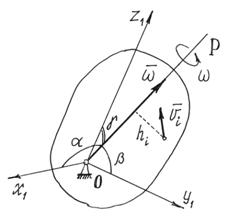
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.47)
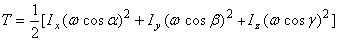
или, окончательно,
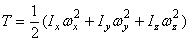 ,
,
где Ix, Iy, Iz – моменты инерции тела относительно главных осей инерции x1, y1, z1 в неподвижной точке О; 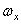 ,
, 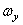 ,
, 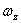 – проекции вектора мгновенной угловой скорости
– проекции вектора мгновенной угловой скорости 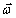 на эти оси.
на эти оси.
 2018-01-08
2018-01-08 2727
2727

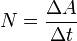 — средняя мощность
— средняя мощность 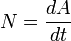 — мгновенная мощность
— мгновенная мощность