Сложение гармонических колебаний

При сложении двух гармонических колебаний, одинаково направленных и одинаковой частоты, описываемых уравнениями

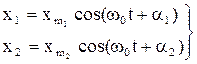, (19)

результирующее колебание будет также гармоническим и иметь частоту w₀:

x = x_mcos(w₀t + a), (20)

где амплитуда x_m и начальная фаза a равны соответственно:

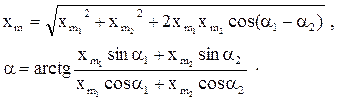(21)

При сложении двух гармонических колебаний одного направления с мало отличающимися частотами, которые задаются уравнениями

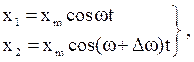(22)

где Dw << w, результирующее колебание является гармоническим с пульсирующей амплитудой. Такие колебания называются биениями.

Уравнение биений имеет вид

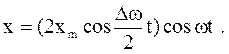(23)

При сложении двух взаимно перпендикулярных колебаний одинаковой частоты, уравнения которых имеют вид

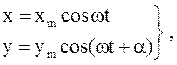(24)

точка движется по траектории

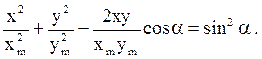(25)

В зависимости от разности фаз a складываемых колебаний возможны частные случаи:

1. a = 0 – точка движется по прямой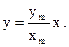

2. a = ±p – точка движется по прямой

В обоих случаях это гармоническое колебание, происходящее по закону

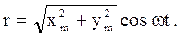(26)

3. a = ±p/2 – точка движется по эллипсу, уравнение которого:

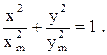(27)

Собственные затухающие механические колебания. Величины, характеризующие быстроту затухания колебаний: коэффициент затухания, логарифмический декремент затухания, добротность, их физический смысл. Апериодический процесс.

Собственными называются свободные колебания, возникающие в колебательной системе в отсутствие сил сопротивления (трения).

Колебания в подобной системе описываются уравнением вида

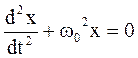, (1)

а сама система называется гармоническим осциллятором.

Примерами гармонических осцилляторов могут служить пружинный, математический и физический маятники (Рис. 1).

 

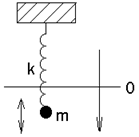
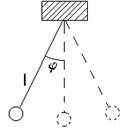
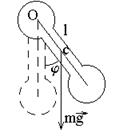
Рис. 1

 

Пружинный маятник – тело массой m, прикрепленное к пружине с жесткостью k.

Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити длиной l.

Физический маятник – тело, совершающее колебания относительно оси О, находящейся на расстоянии l от его центра инерции С.

Для математического и физического маятников роль величины x в уравнении (1) играет угол отклонения j от положения равновесия. При этом гармоническими являются только малые колебания маятников.

Решение уравнения (1) имеет вид

x = x_m соs (w_ot + a), (2)

где x_m – амплитуда колебания, наибольшее значение величины, совершающей колебания;

(w₀t + a) – фаза колебания;

a – начальная фаза, т.е. фаза в момент t = 0;

w₀ – собственная круговая частота колебания (число колебаний за 2p секунд).

Используются также следующие понятия:

T – период колебания (время одного полного колебания). T = 2p/w₀.

n – частота колебания (число колебаний за 1 секунду): .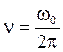

Для рассматриваемых осцилляторов периоды колебаний равны:

пружинного маятника 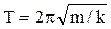; (3)

для математического 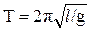; (4)

для физического 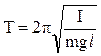. (5)

В формуле (5) величина I – момент инерции физического маятника относительно оси O.

Энергия гармонического осциллятора складывается из кинетической и потенциальной энергий и в любой момент времени остается постоянной:

 

E = kx_m²/2 или E = mw₀²x_m²/2. (6)