Гармонические колебания. Осциллятор.
Колебания массы под действием упругой силы.
Колебания математического маятника.
Тема 7. Колебания и волны.
Решение.
Из формулы (6) получаем, что при 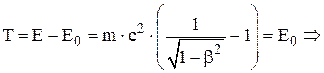
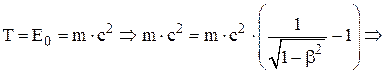
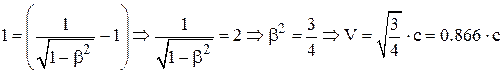
Ответ: в терминах скорости света в вакууме скорость частицы будет равна
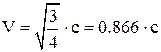 .
.
Примечание. 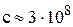 м/c.
м/c.
Лекция №9.
В природе часто встречается периодическая зависимость от времени различных физических величин. Например, мы уже обращались к периодическим колебаниям автомобильного колеса на пружинной подвеске.
Определение 1.
Периодическим называют процесс, при котором физическая величина принимает одинаковые значения через равные промежутки времени. Такие характерные промежутки времени называют периодом процесса.
 При колебаниях периодом является время, в течение которого совершается одно полное колебание.
При колебаниях периодом является время, в течение которого совершается одно полное колебание.
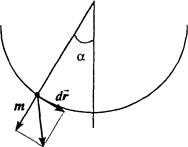
Вычислим период колебаний математического маятника — материальной точки, характеризуемой массой m и подвешенной на невесомой нити длиной l.
При свободном движении маятника в поле силы тяжести (без учёта потерь!) остается постоянной полная энергия маятника — сумма кинетической и потенциальной энергий
E = T + U. Следовательно, при бесконечно малом перемещении маятника вдоль траектории изменение полной энергии должно быть равно нулю.
|
|
|
Изменение потенциальной энергии маятника при его перемещении на расстояние dr можно вычислить как работу силы тяжести на пути dr. При этом работу совершает лишь составляющая силы тяжести вдоль направления движения.
Составляющая силы тяжести, нормальная к направлению движения, работу не совершает. Таким образом, dU = m × g × sin a dr.
Изменение полной энергии (первое слагаемое – это кинетическая, а второе – это потенциальная энергии):
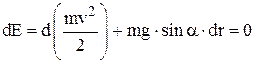 . (1)
. (1)
Произведя дифференцирование и разделив это уравнение сначала на dt, а затем на величину mv = m·dr / dt, получим уравнение движения маятника в виде:
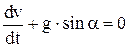 . (2)
. (2)
Удобно перейти к новой переменной – a (угол отклонения маятника!), пользуясь соотношением dr = l d a. Кроме того, при достаточно малых отклонениях можно считать, что 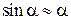 .В этом случае уравнение движения принимает вид:
.В этом случае уравнение движения принимает вид:
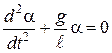 . (3)
. (3)
Решением уравнения (3) является функция (в чем можно убедиться при прямой подстановке!)
a = a0cos(ωt+j0), (4)
где a0 — максимальный угол отклонения маятника, являющийся амплитудой колебаний; ω — угловая частота колебаний, связанная с периодом колебаний соотношением ω=2p/ T; j0 — начальная фаза колебания — величина, характеризующая угол отклонения маятника (a0 · cos j0) в начальный момент его движения (t = 0).
Подставляя выражение (4) в уравнение (3), найдем, что последнее удовлетворяется при значении угловой частоты, называемой собственной частотой колебаний маятника.:
|
|
|
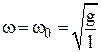 , (5)
, (5)
Таким образом, период колебаний маятника:
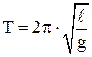 . (6)
. (6)
Особо следует отметить, что период собственных колебаний не зависит ни от амплитуды колебаний маятника, ни от величины колеблющейся массы.
2. Колебания массы под действием упругой силы.
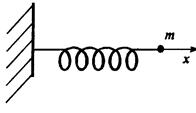 Рассмотрим другой пример малых колебаний вблизи положения равновесия — колебания массы под действием упругой силы. К этой задаче мы также обращались ранее.
Рассмотрим другой пример малых колебаний вблизи положения равновесия — колебания массы под действием упругой силы. К этой задаче мы также обращались ранее.
Если на конце пружины закреплена масса m и пружина характеризуется жесткостью k, то при смещении массы на расстояние x возникает возвращающая упругая сила F = – k×x. Уравнение колебаний массы, полученное из второго закона Ньютона, в этом случае имеет вид:
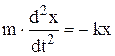 , (7)
, (7)
Уравнение (7) аналогично уравнению (3):
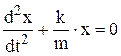 . (8)
. (8)
Собственной частотой колебаний массы на пружине является величина:
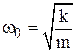 , (9)
, (9)
Решение уравнения (8), то есть, зависимость смещения массы от времени определяется выражением, аналогичным выражению (4):
x (t) = xm ·cos (ω0 t +a0). (10)
 2014-02-09
2014-02-09 1091
1091







