Лекция 4. комплексные числа
К контрольной работе
К началу К следующей лекции
К содержанию К титулу
Содержание
1. Понятие комплексного числа
2. Действия над комплексными числами в алгебраической форме.
3. Геометрическая интерпретация комплексных чисел
4. Тригонометрическая форма комплексного числа.
5. Показательная форма комплексного числа.
6. Решение алгебраических уравнений в пространстве комплексных чисел.
Введение комплексных чисел вызвано тем, что во множестве действительных чисел не выполнено извлечение корня четной степени из отрицательного числа. Комплексные числа являются обобщением действительных чисел.
Пример. Решить квадратное уравнение 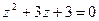 .
.
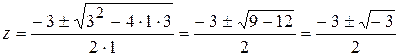 .
.
Мнимая единица 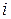 определяется как число, квадрат которого равен (–1). Таки образом,
определяется как число, квадрат которого равен (–1). Таки образом, 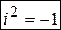 .
.
Учитывая, что 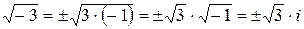 , получаем два комплексных корня:
, получаем два комплексных корня:
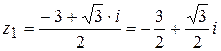 ,
, 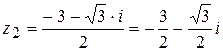 .
.
· Комплексным числом 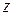 называется выражение вида
называется выражение вида 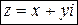 , где
, где 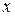 и
и 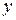 - действительные числа, а
- действительные числа, а 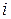 - мнимая единица.
- мнимая единица.
Запись комплексного числа в виде 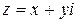 называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
|
|
|
· Действительные числа 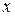 и
и 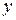 в алгебраической записи комплексного числа
в алгебраической записи комплексного числа 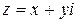 называются действительной и мнимой частямикомплексного числа
называются действительной и мнимой частямикомплексного числа 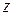 и обозначаются
и обозначаются
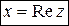 ,
, 
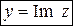 .
.
Если 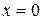 , то
, то 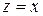 , т.е. комплексное число равно действительному числу. Множество действительных чисел
, т.е. комплексное число равно действительному числу. Множество действительных чисел 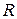 , таким образом, есть подмножество множества комплексных чисел
, таким образом, есть подмножество множества комплексных чисел 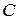 :
: 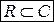 .
.
Если 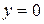 , то число
, то число 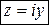 называют чисто мнимым.
называют чисто мнимым.
· Под модулем комплексного числа 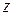 понимается неотрицательное число
понимается неотрицательное число 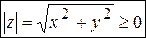 .
.
· Сопряженным числом 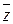 к числу
к числу 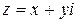 называется комплексное число
называется комплексное число 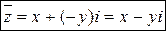 .
.
Пример. Числа 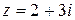 и
и 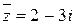 - взаимно сопряженные.
- взаимно сопряженные.
Их модули равны между собой:
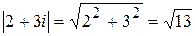 ;
; 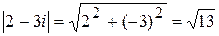 .
.
 2014-01-25
2014-01-25 840
840








