2014-01-25
704
Самый изящный (хотя и нестрогий) способ решения проблемы придумал Маклорен. При этом он предполагал, что f (x) бесконечно дифференцируема. Рассуждения Маклорена были следующими. Предположим, что (1) справедливо. Распишем правую часть этого равенства: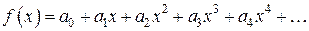
. (2)
Положим что х = 0. Тогда все слагаемые в правой части (2), кроме одного, зануляются, и имеем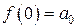 
. Значит, мы нашли первый коэффициент в разложении (1): 
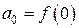. Продифференцируем равенство (2) (его левую и правую части) по х. Имеем:
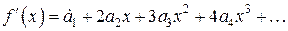. (3)
Хотя производная взята по правилам дифференцирования, именно в этом месте рассуждения Маклорена были нестрогими. Дело в том, что в правой части (2) стоит бесконечная сумма функций (ряд), а правила дифференцирования были доказаны лишь для конечных сумм. Возможность почленного дифференцирования степенного ряда была доказана позже.… Впрочем, сама идея Маклорена была гениальной и верной. Он продолжает свои выкладки.
Положим в (3) х = 0. Тогда опять все слагаемые, кроме одного, зануляются, и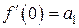 
. Значит, второй коэффициент разложения (1) найден: 
. Далее совершенно аналогичным образом находим: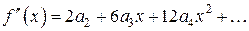
, (4)
|
|
|
откуда получается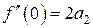 
и 
,
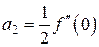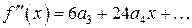, (5)
откуда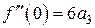 
и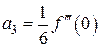 
и так далее.
В результате Маклорен нашел общую формулу коэффициентов степенного ряда для разложения (1):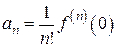 
. (6)
В память об этом успехе разложение f (x) по степеням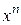 
(т. е. в окрестности точки х = 0) называется рядом Маклорена.
