Цель работы: изучить работу колебательного контура и определить его основные характеристики.
Приборы и принадлежности: осциллограф С1-118, генератор импульсов, набор конденсаторов, катушка индуктивности, переменный резистор.
Изучите теоретический материал по одному из учебных пособий: [1, § 89–90; 2, гл. XXII §22; 3, гл. XI § 51; 4, ч. 2, гл. V §40–41].
Колебательным контуром называется электрическая цепь, состоящая из последовательно соединенных конденсатора емкостью C, катушки индуктивностью L и электрического сопротивления R.
Здесь и далее будем рассматривать так называемый закрытый колебательный контур, в котором электромагнитное поле сосредоточено (локализовано) в той области пространства, где находится контур. Поэтому такой контур не излучает электромагнитные волны в пространство. Будем полагать, что вся индуктивность контура полностью сосредоточена в катушке, а емкость - в конденсаторе. Такой контур называется контуром с сосредоточенными параметрами.
Чтобы возбудить электрические колебания в таком контуре, необходимо создать в нем электрический ток. Реально это можно сделать двумя способами:
|
|
|
сообщить заряд конденсатору;
возбудить индукционный ток в катушке, воздействуя на нее магнитным полем (явление электромагнитной индукции).
При протекании электрического тока в колебательном контуре происходит превращение энергии электрического поля  в энергию магнитного поля
в энергию магнитного поля  и наоборот. В реальных контурах часть энергии всегда выделяется в виде тепла в результате нагревания проводников (закон Джоуля-Ленца). Поэтому электрические колебания в реальном колебательном контуре не могут продолжаться бесконечно долго с одинаковой интенсивностью.
и наоборот. В реальных контурах часть энергии всегда выделяется в виде тепла в результате нагревания проводников (закон Джоуля-Ленца). Поэтому электрические колебания в реальном колебательном контуре не могут продолжаться бесконечно долго с одинаковой интенсивностью.
Для качественного изучения процессов, происходящих в колебательном контуре, рассматривают его упрощенную модель, называемую идеальным колебательным контуром (рис. 9.1). Предполагается, что в идеальном контуре отсутствует активное сопротивление проводников (R =0), поэтому полученная контуром энергия не рассеивается в окружающее пространство в виде теплоты.
Электрические колебания в таком колебательном контуре, по аналогии с механическими колебаниями, описываются дифференциальным уравнением второго порядка.
Если такому контуру сообщить некоторое количество энергии, например, зарядив конденсатор, то в нем возникнут гармонические электрические колебания:
 ,
,
где q – заряд на обкладках конденсатора в момент времени t;
q 0 – амплитудное (максимальное) значение заряда;
w 0 – циклическая частота;
j – начальная фаза.

Рис. 9.1.
Ввиду отсутствия потерь в таком контуре (R =0) колебания будут существовать бесконечно долго без какого-либо воздействия извне. Поэтому они называются свободными или собственными.
|
|
|
Запомните выражения для частоты и периода собственных колебаний:
 ,
,  .
.
Разбирая процессы, имеющие место в реальном контуре, катушка индуктивности которого имеет сопротивление R (рис. 9.2), следует твердо усвоить, что однажды подведенная к нему энергия путем зарядки конденсатора С при каждом колебании будет постепенно расходоваться согласно закону Джоуля–Ленца на нагрев провода катушки индуктивности. Эти потери энергии приведут к затуханию колебаний, амплитуда которых будет убывать с течением времени по определенному закону.

Рис.9.2.
Для выяснения характера изменения во времени колебаний величины заряда конденсатора составим уравнение для контура, согласно второму правилу Кирхгофа:

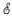 L,
L,
где  – разность потенциалов на обкладках конденсатора;
– разность потенциалов на обкладках конденсатора;
 – сила тока в контуре;
– сила тока в контуре;
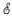 L
L  – ЭДС самоиндукции в катушке индук-
– ЭДС самоиндукции в катушке индук-
тивности.
Тогда
 , или
, или  . (9.1)
. (9.1)
Обозначим 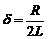 ,
,  . Выражение (9.1) примет следующий вид:
. Выражение (9.1) примет следующий вид:
 .
.
Проанализируйте решение полученного однородного дифференциального уравнения. Им является функция
 , (9.2)
, (9.2)
изображенная на рис. 9.3.

Рис. 9.3.
Амплитуда колебаний величины заряда на обкладках конденсатора  непрерывно уменьшается (затухает) по экспоненциальному закону. Интенсивность затухания амплитуды определяется величиной
непрерывно уменьшается (затухает) по экспоненциальному закону. Интенсивность затухания амплитуды определяется величиной 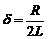 , называемой коэффициентом затухания.
, называемой коэффициентом затухания.
Следует также обратить внимание на влияние сопротивления R в контуре не только на амплитуду заряда, но и на частоту или период колебания:
 . (9.3)
. (9.3)
Необходимо иметь в виду, что в большинстве случаев влияние затухания незначительно, что позволяет считать  . При этих условиях формула (9.3) сводится к формуле
. При этих условиях формула (9.3) сводится к формуле
 , (9.4)
, (9.4)
называемой формулой Томсона.
Если затухание столь велико, что  , колебаний не будет (период Т становится мнимым). Запомните, что такой процесс носит название апериодического.
, колебаний не будет (период Т становится мнимым). Запомните, что такой процесс носит название апериодического.
Следует также знать связь между коэффициентом затухания  и временем затухания
и временем затухания  , в течение которого амплитуда колебаний уменьшается в е раз:
, в течение которого амплитуда колебаний уменьшается в е раз:
 .
.
В лабораторной работе требуется определить величину, характеризующую быстроту затухания и называемую логарифмическим декрементом затухания  , который равен натуральному логарифму двух последовательных амплитуд, разделенных промежутком времени, равным периоду колебаний:
, который равен натуральному логарифму двух последовательных амплитуд, разделенных промежутком времени, равным периоду колебаний:
 .
.
Величина, обратная логарифмическому декременту затухания, показывает, какое количество колебаний N сделает система за время  :
:
 .
.
Важно запомнить, что величина
 , (9.5)
, (9.5)
называемая добротностью колебательного контура, с физической точки зрения, при слабом затухании определяет отношение энергии W, запасенной в контуре, к убыли этой энергии  за один период колебания:
за один период колебания:
 .
.
 2018-02-13
2018-02-13 443
443








