Безвихревое (потенциальное) движение жидкости

1. Потенциал скорости и функция тока. Движение жидкости называется безвихревым, если

                                                                               (2.25)

во всей области течения. Напомним, что ротор векторного поля  определяется формулой

                          

В этом случае поле скоростей можно представить в виде градиента некоторой скалярной функции:

                                          .                                  (2.26)

Функция  называется потенциалом скорости. Таким образом, безвихревое движение жидкости оказывается потенциальным. Верно и обратное.

Рассмотрим плоское установившееся безвихревое течение идеальной несжимаемой жидкости в поле консервативных массовых сил. Для описания такого движения имеем:

• уравнение неразрывности

                                       ;                              (2.27)

• условие отсутствия вихрей (2.25)

                                       ;                               (2.28)

• интеграл Бернулли в форме (2.18)

                                   .                          (2.29)

Выведем уравнение для потенциала скорости. Согласно (2.26)

                                    , .                            (2.30)

Подставим соотношения (2.30) в уравнение неразрывности (2.27):

                                       .                               (2.31)

Граничными условиями для уравнения (2.31) являются:

– на поверхности  обтекаемого тела , т.е. , где 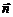 – вектор нормали;

– на бесконечности , т.е. , , где  – скорость невозмущенного потока.

Таким образом, для определения 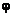 необходимо решить задачу Неймана для уравнения Лапласа – потенциал скорости является гармонической функцией.

Заметим далее, что уравнение неразрывности (2.27) выполняется тождественно, если

                                   , ,                          (2.32)

где  – некоторая функция. Полный дифференциал  равен

                        .               (2.33)

Сравнивая (2.33) с уравнением линий тока (2.3) в плоском течении, видим, что вдоль линий тока

                                    , .

Функция  называется функцией тока. Равенство  дает уравнение линии тока и, в частности, контура обтекаемого тела:

                                      ,

где 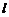 – координата вдоль контура. Отсюда  на границе тела. С помощью функции  можно рассчитать расход жидкости, протекающей через произвольную кривую AB (рис. 2.6):

                   ,

т.е. расход жидкости через кривую равен разности значений функции тока на концах этой кривой.

Подчеркнем, что для того чтобы ввести функцию тока, вообще говоря, не требуется потенциальность потока. Для определения  без­вихревого течения необходимо решить задачу Дирихле для уравнения Лапласа, т.е. функция тока, как и потенциал, является гармоничес­кой функцией.

2. Комплексный потенциал. Сравним выражения для составляющих скорости согласно (2.30) и (2.32):

                                  , .

Это известные из теории функций комплексного переменного условия Коши–Римана, которые гарантируют, что функция

                            

является аналитической функцией комплексного аргумента . Функция  называется комплексным потенциалом течения. Нетрудно показать, что

                                    ,                            (2.34)

т. е. производная  совпадает с сопряженной комплексной ско­ростью.

Как было показано выше, при безотрывном обтекании твердой стенки идеальной жидкостью эта стенка является линией тока. Поэтому в течении с каким-либо комплексным потенциалом можно любую линию тока заменить твердой стенкой и  будет описывать обтекание этой стенки (принцип отвердевания). Поясним на примере.

Рассмотрим потенциал

                                   .                           (2.35)

Отделяя действительную и мнимую части, находим:

               ,

т.е. линии тока определяются соотношением

                       .

Например, при :

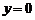               , т.е.  и .

Как видно, линией тока данного течения является, в частности, окружность. Поэтому согласно принципу отвердевания комплексный потенциал (2.35) описывает обтекание бесконечного круглого цилиндра радиуса .

Проанализируем картину течения. Сопряженная комплексная скорость

                                 ,

с другой стороны, . Поэтому при  получаем , т.е. , . Это означает, что скорость натекающего на цилиндр потока равна на бесконечности  и параллельна оси  (рис. 2.7). Компоненты скорости равны:

           , , (2.36а)

или в полярных координатах , :

               , .    (2.36б)

Полагая в (2.36б) 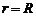, получаем скорость на поверхности цилиндра:  (т.е. обтекание безотрывное), .

В точках A и B скорость равна нулю, эти точки – критические.
В точках  и  скорость имеет наибольшую вели­чину, равную  – удвоенной скорости набегающего потока.

Для оценки силового воздействия потока на тело найдем коэффициент давления  согласно уравнению Бернулли (2.29):

                                       ,

т. е. на поверхности цилиндра

                                      .

На контуре САD в передней критической точке А коэффициент давления имеет максимальное значение, затем при движении к точкам С и D происходит разгон жидкости от нуля до . Это конфузорная часть контура. На участке СВD скорость падает и давление растет – это диффузорная часть контура.

Картина обтекания кругового цилиндра симметрична относительно как оси Оx, так и оси Oy. Поэтому главный вектор сил давления жидкости на цилиндр равен нулю.

Данный результат называется парадоксом Даламбера: при обтекании идеальным потоком тела реакция между ним и потоком отсутствует. Парадокс Даламбера опровергается при рассмотрении реального вязкого течения с образованием вихрей в пограничном слое вокруг тела, с отрывом слоев вблизи миделевых точек D и С (см. раздел 5).

Н.Е. Жуковский показал, что если идеальный поток обтекает круговой цилиндр, имеющий вращение, то возникает подъемная сила.

Рис. 2.7. Обтекание кругового цилиндра