Кручення просторової кривої

Формули Серре-Френе

Співдотична площина просторової кривої при переміщенні вздовж кривої не залишається постійного напрямку; зміну її напрямку можна охарактеризувати зміною напрямку перпендикулярного до неї вектора - одиничного вектора бінормалі.

Зміна напрямку вектора характеризується вектором , який називають вектором другої кривизни або вектором кручення просторової кривої. Модуль цього вектора дорівнює границі відношення кута суміжностей бінормалей (кута, на який повертається бінормаль при переході від даної до сусідньої точки кривої) до довжини відповідної дуги кривої, коли довжина дуги прямує до нуля:

,

тобто швидкості обертання вектора при переміщенні точки по кривій. Знайдемо вектор .

Диференціюємо рівність :

.

Але , тому . Отже,

.

Звідси випливає, що є вектор, що перпендикулярний до вектора (за означенням векторного добутку) і до вектора , як до одиничного вектора). Значить колінеарний вектору Позначивши довжину вектора через , тобто , будемо мати

(7.33)

Скалярний множник при в правій частині формули (7.33) називають крученням просторової кривої. д - кручення, радіус кручення.

Знайдемо вектор . Для цього диференціюємо рівність :

,

або

Формули

(7.34)

називаються формулами Серре-Френе, це основні формули геометрії просторових кривих.

Виведемо формули для кривизни та кручення просторової кривої, яка задана векторним рівнянням .

Перша із формул Серре-Френе дає

, (7.35)

оскільки . Домножимо другу із формул Серре-Френе скалярно на вектор :

.

Але

,

,

тому

.

(7.36)

В координатній формі ці формули мають такий вигляд

(7.37)

Якщо вектор заданий як функція довільного параметру (а не довжини дуги ), то формули (7.35) і (7.36) набувають вигляду:

(7.38)

Вектори, колінеарні одиничним векторам та будемо позначати та . Щоб написати рівняння дотичної, головної нормалі, бінормалі та будь-якої із площин супроводжуючого тригранника, достатньо лише в канонічних рівняннях прямої

(7.39)

і в рівнянні площини, яка проходить через дану точку

, (7.40)

взяти за координати вибраної на просторовій кривій точки, а за та або відповідно та - координати того із векторів або , який визначається напрямком шуканої прямої або нормалі до шуканої площини: або для дотичної та нормальної площини, і - для головної нормалі та спрямної площини, або - для бінормалі та співдотичної площини.

Нехай просторова крива задана векторним рівнянням 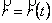, або, що те саме, рівнянням

.

За вектор , який має напрямок дотичної до кривої, можна взяти вектор .

Отже,

. (7.41)

Для відшукання векторів , що мають напрямок головної нормалі та бінормалі, знайдемо спочатку розклад вектора за векторами .

Оскільки

.

то

. (7.42)

Перемножимо вектори та :

(7.43)

Звідси

(7.44)

Тоді за вектор через його перпендикулярність до векторів та можна взяти векторний добуток цих двох векторів:

(7.45)

Цим самим ми дістали можливість в будь-якій точці просторової кривої визначити всі елементи його супровідного тригранника.