С заданными законами распределения вероятностей
Для формирования значений случайной величины Х с произвольным законом распределения вероятностей используются реализации случайной величины R~[0,1). Существуют две группы методов преобразования случайной величины R:
1. Прямые методы, которые состоят в выполнении некоторой операции над случайной величиной R, формирующей случайную величину Х, имеющую точно или приближенно заданный закон распределения вероятностей.
2. Приближенные методы, которые основываются на моделировании условий соответствующей предельной теоремы теории вероятностей, или на аппроксимации функции распределения.
Прямые методы
1.1.Метод обратной функции. Реализует преобразование случайной величины R с помощью некоторой функции X = φ(R).
Идея преобразования вытекает из следующей теоремы. Если случайная величина Х имеет плотность распределения f(x), то случайная величина R с реализациями 
 равномерно распределена на интервале [0,1), т.е. всякую непрерывную случайную величину можно преобразовать в случайную величину, равномерно распределенную на интервале [0,1).
равномерно распределена на интервале [0,1), т.е. всякую непрерывную случайную величину можно преобразовать в случайную величину, равномерно распределенную на интервале [0,1).
|
|
|
Справедливо и обратное. Если F(x) – функция распределения непрерывной случайной величины Х, а R – случайная величина с равномерным распределением на интервале [0,1), то случайная величина Х=F-1(R) имеет функцию распределения F(x), где F-1 – функция, обратная по отношению к F. Рисунок 1 иллюстрирует нахождение функции распределения F(x) случайной величины X (1).
P(X<x) = P(F-1(R)<x) = P [F(F-1(R))<F(x)] = P(R<F(x))=  (1)
(1)
| F(x) |
| x |
| x |
| X |
| 0 |
| R R |
| F(x) |
| 1 |
Рисунок 1 – Функция распределения F(x) случайной величины X.
Таким образом, последовательность r1, r2, r3, …, принадлежащая R[0,1), преобразуется в последовательность x1, x2, x3, …, имеющую заданную плотность распределения f(x).
Значение xi случайной величины X является решением уравнения
F(xi) = ri (2)
Соответственно,
xi=F-1(ri). (3)
Алгоритм получения случайной величины с заданной функцией распределения F(x):
· получить реализацию ri~[0,1);
· вычислить значение реализации xi по формуле (3).
1.1.1. Моделирование случайной величины с экспоненциальным законом распределения вероятностей.
| f(x) |
| F(x) |
| x |
| x |
Формулы (4) и (5) задают плотность и функцию распределения случайной величины с экспоненциальным законом распределения.
 (4)
(4)
 (5)
(5)
Решая уравнение (2), находим обратную по отношению к F функцию:

 (6)
(6)
|
|
|
Т.к. случайная величина (1-R) имеет такое же распределение, как и случайная величина R, от (6) переходим к (7).
 (7)
(7)
1.1.2. Моделирование случайной величины с равномерным законом распределения вероятности.
| x |
| x |
| a |
| b |
| a |
| b |
| F(x) |
| f(x) |


xi=a + (b-a) * ri (5)
1.2. Методы, основанные на преобразовании равномерно распределенной случайной величины.
1.2.1 Моделирование случайной величины с дискретным распределением, с ограниченным спектром значений.
Случайная величина

имеет дискретное распределение

Преобразование равномерно распределенной CВ к дискретной производится с помощью функции (6):
 (6)
(6)
Для такого преобразования используется инверсная функция распределения вероятностей:
| FI |
| Xn |
| Xk |
| Xk-1 |
| X1 |
| X0 |
| p0+p1 |
| p0 |

|
| r |

|

|

|
Моделирование случайной величины сводится к розыгрышу значений, которые случайная величина может принимать. Розыгрыш заключается в том, что каждому значению ставится в соответствие событие, вероятность наступления которого совпадает с вероятностью данного значения случайной величины.
Область определения случайной величины R делится на подинтервалы  k, такие что длина интервала
k, такие что длина интервала  k равна pk. Тогда вероятность попадания реализация ri случайной величины R в интервал
k равна pk. Тогда вероятность попадания реализация ri случайной величины R в интервал  k, равна pk, т.е. p{
k, равна pk, т.е. p{  } = pk. Алгоритм моделирования случайной величины основан на формальной идентичности событий:
} = pk. Алгоритм моделирования случайной величины основан на формальной идентичности событий:
X=xk и 
if ri<=p0 then xi=x0
else if ri<=p0+p1 then xi=x1
…
else if ri<= 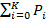 then xi=xk
then xi=xk
…
else xi=xn
1.2.2 Моделирование случайной величины с дискретным законом распределения вероятностей с неограниченным спектром значений (СВ с законом Пуассона).

Алгоритм моделирования №1:
1. 
2.  , где
, где  (7)
(7)
3. Если неравенство (7) выполняется, X=k.
Приближенные методы
2.1 Методы, основанные на воспроизведении условий соответствующей предельной теоремы теории вероятности
2.1.1 Моделирование случайной величины с нормальным законом распределения вероятности
На основании центральной предельной теоремы реализация СВ с нормальным законом получится как сумма n независимых реализаций равномерно распределенной СВ.


Достаточным считается n=12, следовательно: M(norm)=6, D(norm)=1
Для получения нормированной нормальной СВ необходимо выполнить центрирование:
N(0,1) nnorm=norm-6
В общем случае, когда n<>12, необходимо выполнить центрирование и нормирование.

| центрирование |
| нормирование |
Для получения реализаций с произвольным математическим ожиданием и дисперсией используется формула (8):
 (8)
(8)
2.1.2 Моделирование случайной величины, распределенной по закону Пуассона
Алгоритм моделирования №2
Основываемся на соотношении между экспоненциальным распределением и распределением Пуассона. Если интервалы времени между появлениями событий распределены по экспоненциальному закону, то число событий на этом интервале распределено по закону Пуассона.
Если реализации СВ Y y1,y2,… независимы м имеют экспоненциальное распределение с математическим ожиданием 1, то неотрицательное целое число k, для которого выполняется (9), является реализацией СВ, распределенной по закону Пуассона с параметром  :
:
 (9)
(9)
Так как реализация СВ с экспоненциальным законом распределения и математическим ожиданием = 1 определяется как yi=-ln ri,  , то
, то
|
|
|
 или
или
 (10)
(10)
Алгоритм получения СВ, распределенной по закону Пуассона:
1) Получить последовательности {ri} независимых случайных величин, равномерно распределенных на [0,1)
2) Вычислять произведения  до тех пор, пока не выполнится (10)
до тех пор, пока не выполнится (10)
3) при выполнении (10) значение СВ X = k.
2.1.3 Моделирование СВ с биномиальным законом распределения вероятностей
Биномиальное распределение является распределением вероятности появления k событий в n независимых испытаниях, в каждом из которых вероятность появления события равна р.
Моделирующий алгоритм основан на представлении реализаций СВ с биномиальным законом в виде суммы n независимых реализаций СВ Y, имеющей распределение yi:
yi 1 0
pi p 1-p
Алгоритм получения реализаций СВ Х, распределенной по биномиальному закону:
1) получить реализацию ri СВ, распределенной равномерно на [0,1)
2) для каждой реализации ri проверить выполнение неравенства ri<p, i=1,2,…,n
3) вычислить сумму n реализаций СВ Y и принять эту сумму за реализацию СВ Х,
 , имеющий смысл числа успехов в вероятностной схеме испытаний Бернулли (11)
, имеющий смысл числа успехов в вероятностной схеме испытаний Бернулли (11)
2.2 Методы, основанные на аппроксимации функции распределения
На практике часто бывает необходимо получить распределение СВ по эмпирической функции распределения, построенной на основе некоторой статистической информации, собранной на модели или реальной системе. В этом случае функция распределения F(x) аппроксимируется некоторой функцией G(x), обратная функция от которой G-1(x) имеет достаточно простое аналитическое выражение и легко вычислима. Чаще всего вместо определения функции G(x) используется кусочно-линейная аппроксимация. Для этого интервал изменения функции F(x) разбивается на n подинтервалов, число которых определяется требуемой точностью конечных результатов. На каждом из подинтервалов рассматривается линейный участок аппроксимирующей функции G(x) и используется метод обратной функции.
|
|
|
Пример. Пусть о СВ Х собрана следующая статистика: 30% значений в диапазоне [10,20],
40% значений - ]20;30]
30% значений - ]30,40]
Функция моделирования СВ Х, образованная путем инверсии F(x), имеет вид:
| 0.3 |
| 0.4 |
| 1 |
| 0 |
| 10 |
| 20 |
| 30 |
| 40 |
| FI |
| r |
Моделирующий алгоритм:
ri
if ri <=0.3 then FI=10+(20-10)*ri/0.3
else if ri <=0.7 then FI=20+(30-20)*(ri-0.3)/0.4
else FI=30+(40-30)*(ri-0.7)/0.3
или
if ri <= 0.3 then FI=10+10*ri
else if ri<=0.7 then FI=20+10*ri
else FI=30+10*ri
 2020-01-15
2020-01-15 150
150








