И требуется перебрать комбинации Х, У – чётные - нечётные числа

Итого 16 вариантов. Плюс варианты гипотезы Биля.

И если всё это обилие решать количественно, - это уже приличная работа для издания отдельной брошюры, а не публикации в формате статьи.

Вариант I.

1. А > В, Х < У Х – чётное число, У – чётное число.

Основания и показатели расписываю за один заход.

, где конечно же ₁> ₂, а ₁ < ₂.

Вначале разбираемся с показателями

На второй стадии пройдусь по основаниям

Равенство левой и правой части уравнения невозможно.

Тогда и исходное уравнение решений не имеет.

2. А > В, Х < У Х – нечётное число, У – нечётное число.

Во всех решениях вначале степень, затем основание

Решим полученное условие относительно А и В.

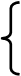
После подстановки А=В+1.

Т.е., чтобы уравнение А^х-В^у=1 существовало при заданных условиях д.б. А=В+1.

3. А > В, Х < У Х – чётное число, У – нечётное число.

После преобразований

Далее вывод, как и в примере (1).

4. А > В, Х < У Х – нечётное число, У – чётное число.

Результат, как и в примере (2).

5. А < В, Х > У Х – чётное число, У – чётное число.

Нет решения, ибо это формула разности квадратов.

6. А < В, Х > У Х – нечётное число, У – нечётное число.

Решение у такой формулы возможно.

7. А < В, Х > У Х – чётное число, У – нечётное число.

Противоречий для существования данной формулы нет.

8. А < В, Х > У Х – нечётное число, У – чётное число.

И окончательно.

Запрета на существование такого уравнения не вижу, но дальнейший анализ не в этой статье.

Вариант II.

9. А > В, Х < У Х – чётное число, У – чётное число.

Уравнение разности квадратов - тогда решений не существует.

10. А > В, Х < УХ – нечётное число, У – нечётное число.

Уравнение реальное - тогда решение есть.

11. А > В, Х < У Х – чётное число, У – нечётное число.

Уравнение реальное.

Пример: 3²-2³=1

12. А > В, Х < У Х – нечётное число, У – чётное число.

Решение существует.

13. А < В, Х > У Х – чётное число, У – чётное число.

14. А < В, Х > У Х – нечётное число, У – нечётное число.

15. А < В, Х > У Х – чётное число, У – нечётное число.

16. А < В, Х > У Х – нечётное число, У – чётное число.

(а)

Для случаев 13, 14, 15, 16 итоговое уравнение одинаковое.

Рассмотрим эти четыре случая чуть подробнее.

, тогда

После подставим в уравнение (а) получим

, при начальном условии .

Тогда варианты 13, 14, 15, 16 – не верны.

Из рассмотренных выше задач, при всех вариантах начальных условий, - 8 задач решений в целых числах не имеют.

Для закрепления материала предлагаю рассмотреть два заведомо не имеющих решения уравнения.

Первый пример.

Пусть: А - чётное число.

В - нечётное число.

А > В, Х > У, Х – чётное число, У – нечётное число.

Основное противоречие состоит в условии А > В, Х > У.

, что, конечно же, не возможно, т.к. левая часть всегда больше правой.

Второй пример.

Пусть: А - нечётное число.

В - чётное число.

А > В, Х > У, Х – чётное число, У – нечётное число.

После соответствующих преобразований

что, конечно же, не возможно.

Гипотеза Биля (ГБ).

, где А, В, С – взаимно простые числа и Х, У, Z > 2.

Рассмотрим 2 варианта:

- I А - чётное число, В - нечётное число, С - нечётное число;

- II А - нечётное число, В - чётное число, С - нечётное число.

Строго говоря, чтобы полностью разобрать ГБ, надо рассмотреть все варианты решения уравнений.

Но дело в том, что новый метод исследования диофантовых уравнений говорит о том, что ГБ не верна, т.е. уравнение при некоторых сочетаниях А, В, С, Х, У, Z может иметь место. По этому будет рассмотрено лишь два примера, которые указывают на возможность решения уравнения.

Вариант I.

а) Пусть А > В > С, и Х < У < Z, и А - чётное число, В - нечётное число, С - нечётное число.

Составим функциональное уравнение.

Подразумевая систему функциональных уравнений, возьмём к = - ₃

(1)

Возьмём обозначение

Уравнение (1) примет вид уравнения Каталана

И именно из этого и следует наличие решений у уравнения ГБ.

Вариант II.

а) Пусть А > В > С, и Х < У < Z, где Х, У – нечётные числа, А - нечётное число, В - чётное число, С - нечётное число.

Составим функциональное уравнение.

Решая относительно основания, получим

Проведу преобразование в показателях

После упрощения.

Вполне реальное уравнение, которое должно иметь место.

В настоящей работе представлен сравнительно небольшой анализ. Более серьёзным анализом займусь в зиму 2009-2010 годов.

И приведу один контр пример.

Заведомо противоречивое начальное условие – в примере (а) пусть

Х > У > Z.

Тогда в уравнении Каталана

И тогда не может иметь место знак равенства.

Т.е. задача с заведомо неверными начальными условиями исключается сразу.

Вот почему и есть основание верить в решения в целых числах у уравнения ГБ.

Заключение.

Данному алгоритму на момент появления в интернете всего два месяца. Дитё.

Что можно нарешать за два месяца? А больше я себе не могу позволить заниматься не профилирующим предметом в моей трудовой деятельности.

Напоследок хочу коснуться одной практической проблемы при решении Диофантовых уравнений данным методом.

Сколько раз можно «бить» по уравнению, представленным алгоритмом?

Можно по отношению к конкретному уравнению теоретически на единицу меньше, чем число неизвестных в данном уравнении.

Первая стадия – убираем самое меньшее неизвестное. А на второй стадии уже надо знать разницу между оставшимся самым маленьким числом, и предстоящим. Или же не зная этой разницы, вводить параметр.

Почему это происходит?

На первой стадии мы наши неизвестные приблизим к началу числовой оси. Если самое наименьшее число чётное, то оно будет находиться на позиции «два», а если не чётное – то на позиции «один».

И чтобы ещё по уравнению пройтись представленным алгоритмом, надо все неизвестные «откатить» от начала числовой оси на несколько шагов. Приведу простейший пример.

Пусть есть уравнение Х³+У³+Z³=6903

И пусть каким - то одним нам известным способом мы узнаём, что Х, У, Z – нечётные и следуют подряд.