Структурні теореми. Порядки симплектичних груп

Пропозиція 32 Якщо поле нескінченно, те групи , над також нескінченні.

Доказ. Число трансвекцій з нескінченно.

Теорема 33 Порядок групи дорівнює

Порядок групи дорівнює

Доказ. Друге твердження треба з першого, тому що група ізоморфна групі . Доведемо перше твердження індукцією по . Якщо , то й можна вважати .

Під парою будемо розуміти впорядковану пару векторів , , таку, що . Якщо фіксовано, то існує єдина пара , де належить даній прямій, не ортогональної к. Тому число пар з на першому місці дорівнює числу прямих, що не лежать в , тобто

Таким чином, є пара з на першому місці, а всього пара.

Зафіксуємо яку-небудь пару . По теоремі Витта для кожної пари найдеться принаймні один елемент групи , що переводить в. Отже, є точно

елементів з , що переводять пари в парі . По припущенню індукції це число дорівнює

Далі, кожний елемент групи переводить точно в одну пару. Отже, група містить

елементів, що й було потрібно довести.

Пропозиція 34Якщо , те число максимальних цілком вырожденных підпросторів простору дорівнює

Доказ.1) Покажемо спочатку, що підгрупа групи , що залишає на місці довільне максимальне цілком вироджений підпростір простору , має порядок

Щоб переконатися в цьому, зафіксуємо симплектичну базу

простору , у якій вектори породжують . Із треба, що матриця довільного перетворення має вигляд

де , а - симетрична матриця порядку над ; ці й визначаються перетворенням однозначно. Крім того, будь-які такі й відповідають якомусь із . Наше твердження виходить тепер, якщо помножити порядок групи на число симетричних матриць порядку над полем , тобто .

2) Зафіксуємо максимальне цілком вироджений підпростір простору . По теоремі Витта всі максимальні цілком выроджені підпростору простору даються формулою , де пробігає групу . Із зауваження 1) легко треба, що в цьому процесі кожне максимальне цілком вироджений підпростір повторюється точно

раз, тому загальне число таких підпросторів дорівнює порядку групи , діленому на зазначену величину. Очевидно, це і є необхідне число.

Пропозиція 35 Якщо , те число регулярних площин у просторі дорівнює

Доказ. Надходячи, як при доказі твердження, переконаємося, що повинне містити

регулярних площин. Це число збігається із зазначеним вище (застосувати теорему).

Пропозиція 36 Група ізоморфна симетричній групі .

Доказ. Будемо називати конфігурацією довільна підмножина з елементів в - мірному регулярному знакозмінному просторі над полем , що володіє тим властивістю, що будь-які два його різних елементи не ортогональні. Кожний ненульовий вектор з належить рівно двом конфігураціям і , так що вони перетинаються по . Щоб переконатися в цьому, візьмемо симплектическую базу простору , у якій . Ясно, що

дві різні конфігурації, що перетинаються по множині . Легка перевірка перебором показує, що інших конфігурацій, що містять елемент , немає. Якщо тепер виписати всі різні конфігурації в просторі , то кожний вектор із з'явиться точно у двох з них, звідки й . Нехай - Множина всіх конфігурацій в.

Якщо - довільний елемент із , то тоді й тільки тоді є конфігурацією, коли - конфігурація, тому індуцирує відображення . Ясно, що це відображення на й, виходить, перестановка на . Очевидно, що є гомоморфне відображення . Щоб знайти його ядро, візьмемо в елемент . Нехай такий, що . Нехай і - дві конфігурації, що містять . Тоді не належить однієї з них, скажемо, . Звідси й . Інакше кажучи, ядро тривіально, і ми маємо інективный гомоморфізм . По теоремі група складається з елементів, тому .

Центри

Помітимо, що група неабелева. Щоб переконатися в цьому, досить взяти нетривіальні проективні трансвекції із із прямими. Отже, група також неабелева.

Пропозиція 37 Група має тривіальний центр, а .

Доказ. Розглянемо довільний елемент із центра групи . Нехай - довільна пряма з . Нехай - проективна трансвекція із із прямій . Тоді прямій перетворення є . Але , тому що лежить у центрі. Отже, для всіх . Тому й, виходить, група дійсно не має центра. Друге твердження треба з першого, якщо застосувати гомоморфізм .

Комутанти

Пропозиція 38 Якщо , - довільні прямі з , та множина трансвекцій із із прямої й множину трансвекцій з прямій сполучені відносно .

Доказ. По теоремі Витта в групі існує такий елемент , що . Тоді сполучення елементом відображає множина трансвекцій із із прямій на множину трансвекцій із із прямій .

Приклад 39 Дві трансвекції з не обов'язково сполучені в. Наприклад, трансвекції з прямій , сполучені з , мають вигляд , де пробігає .

Зауваження 40 Нехай - симплектическая база простору . Якщо - довільна симетрична матриця порядку 2 над і - лінійне перетворення, певне матрицею те ми знаємо, що належить групі . Якщо перетворити в , роблячи 1) додаток кратного одного стовпця до іншого з наступним аналогічним перетворенням відповідних рядків або 2) перестановку двох стовпців з наступною перестановкою відповідних рядків, то лінійне перетворення з матрицею знову буде належати групі , тому що теж буде симетричною. У дійсності й сполучені в. Щоб переконатися в цьому, помітимо, що при підходящій матриці з . Перетворення , певне матрицею належить групі , і , тому що .

Пропозицію 41 Припустимо, що , , і нехай - нормальна підгрупа групи , що містить регулярний елемент із відрахуванням , у вигляді добутку двох трансвекцій з . Тоді .

Доказ. Маємо розкладання , де - регулярна площина. Розглянемо групу

Тоді . Крім того, . Це очевидно, якщо ; якщо ж , те застосовуємо 2.1.12 і теорему 2.1.11. Тому - нормальна підгрупа в , що не втримується в. Звідси треба, що . Зокрема, якщо - фіксована пряма в , те містить всі трансвекції площини з прямій . Отже, містить всі трансвекції із із прямій , а тому в силу взагалі всі трансвекції з і .

Пропозицію 42 Припустимо, що , або , , і нехай - нормальна підгрупа групи , що містить елемент із відрахуванням 2, у вигляді добутку двох трансвекцій з . Тоді .

Доказ.1) Модифікація міркувань, використаних при доказі твердження, дозволяє вважати, що , якщо , і , якщо .

2) Розглянемо спочатку випадок , . Тоді має вигляд , причому , а зірочки рівні . Далі ці трансвекції перестановочні, тому що , тому ми можемо, якщо потрібно, замінити на й уважати, що насправді . Можна вважати, що ця нова є . Справді, якщо , те за допомогою теореми Витта виберемо таке , що , . Тоді . Замінимо тепер на . Отже, можна вважати, що . Доповнимо до симплектичної бази

простору й помітимо, що

Підходящим сполученням ми можемо знайти в лінійні перетворення з матрицями

у базі . Добуток цих перетворень дорівнює елементу із із матрицею

Отже, група містить . Таким чином, вона містить всі (= обидві) трансвекції із із прямій . Через звідси треба, що містить всі трансвекції з і, виходить, .

3) Нехай тепер , . Тоді й . Доповнимо до симплектичної бази Тоді

Сполучення дає нам у лінійні перетворення з матрицями

а тому й з матрицями

а виходить, і з матрицею

Інакше кажучи, містить і, отже, всі трансвекції з , звідки . Пропозиція 43 Якщо , те за одним виключенням: . Доказ. Нехай , для якогось . По теоремі Витта існує таке , що - площина й

Покладемо

Залишилося застосувати й. У винятковому випадку застосовуємо й добре відомі властивості групи .

Пропозиція 44 Якщо , те за одним виключенням: .

Теореми про простоту

Теорема 45 Для будь-якого парного числа й кожного поля група проста за винятком групи , що простій не є.

Доказ.1) Виняткове поводження групи треба з. Будемо припускати тому, що в загальному випадку й при . Замість проективної групи ми будемо мати справу із групою . Досить розглянути нормальну підгрупу групи , що не втримується в підгрупі , і довести, що .

2) Спочатку покажемо, що є , , такі, що - регулярна площина. Для цього візьмемо в групі елемент. зрушує принаймні одну пряму з , тобто існує така пряма з , що . Нехай - нетривіальна трансвекция із із прямій . Тоді елемент належить групі і є добутком двох трансвекцій із із різними прямими й . Тому простір перетворення є площина , зокрема, . Якщо - гіперболічне перетворення, то - інволюція. Застосуємо тепер твердження 1.18, якщо характеристика дорівнює , і твердження 1.13, якщо характеристика не дорівнює . Тоді, зокрема, ми одержимо, що не є добутком трансвекції з , що суперечить допущенню. Отже, не може бути гіперболічним. Виходить, існує такий вектор , що , тобто - регулярна площина.

3) Можна також показати, що є вектор і перетворення , такі, що - вироджена площина. Справді, візьмемо в елемент . Існує такий вектор , що .

Якщо , то ціль досягнута, тому будемо вважати, що .

Виберемо так, щоб було

По теоремі Витта в найдеться перетворення , таке, що , . Тоді перетворення належить і переводить в , тому - вироджена площина.

4) Візьмемо , так, щоб площина була регулярної при й виродженій при . Тоді перетворення

належить групі , є добутком двох трансвекцій з і його простір є площина . Тому .

Пропозиція 46 Якщо й - нормальна підгрупа групи , те або , за винятком групи , що, мабуть, не має цю властивість.

Доказ. Із приводу виключення див.. Далі, застосовуючи до теорему, одержимо, що або . Допустимо останнє. Тоді

Пропозиція доведена.

Теорему про простоту можна також довести, використовуючи групи підстановок. Нагадаємо, що групою підстановок непустої множини називається підгрупа групи всіх підстановок множини . Далі, називається транзитивної, якщо для будь-яких , існує така підстановка з , що . Нагадаємо, що розбивкою множини називається множина 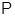попарно непересічних підмножин, об'єднання яких дорівнює . Тривіальними називаються дві розбивки, що складаються відповідно із самого й із всіх одноелементних підмножин. Транзитивна група підстановок множини , якщо існує така нетривіальна розбивка 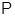множини , що для всіх , . У противному випадку група називається примітивної. Наступний результат є тут ключовим.

Пропозиція 47 Примітивна група підстановок множини проста, якщо виконані наступні умови:

1) ,

2) для якогось стабілізатор містить таку нормальну абелеву підгрупу , що породжується підгрупами , .

Для доказу теореми з використанням цього результату розглянемо як групу підстановок множини прямі простори . Це можливо через те, що , будучи підгрупою групи проективностей простору , точно діє на й, виходить, природно ізоморфна групі підстановок множини . Ми знаємо, що група транзитивна (теорема Витта), (див.) і, нарешті, множина проективних трансвекцій із із прямій разом з тотожним перетворенням утворить нормальну абелеву підгрупу стабілізатора прямій в , що разом зі своїми сполученими в породжує групу . Тому все, що залишилося зробити, перш ніж послатися на, - це перевірити, що група примітивна.

Пропозиція 48 При група підстановок множини прямі простори примітивна.

Доказ.1) Розглянемо розбивку 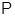множини , що містить принаймні дві підмножини, одне із яких, скажемо , містить не менш двох прямих. Нам потрібно знайти елемент групи , що не зберігає цю розбивку. Допустимо, що такого елемента не існує.

2) Нехай спочатку містить дві різні не ортогональні прямі , . Тоді кожні дві різні прямі , з повинні бути не ортогональні. Справді, якщо це не так, то найдуться різні , з , такі, що . Візьмемо пряму з , не приналежній підмножині . Якщо , то по теоремі Витта існує таке перетворення з , що , , і, отже, воно порушує розбивку. Якщо , то знову по теоремі Витта є таке , що , і, виходить, знову порушує розбивка. Отже, ніякі дві різні прямі з не є ортогональними. Тільки що проведені міркування показують, що якщо - довільна пряма з , те містить всі прямі з , не ортогональні к. Тепер очевидно, що можна знайти в пряму , не ортогональну до , але ортогональну до тоді перша умова спричиняє, що , а друге - що , - протиріччя.

3) Ми можемо, таким чином, уважати, що всі прямі з попарно ортогональні. Міркування, використані в п.2), показують тоді, що якщо - довільна пряма з , те містить всі прямі, ортогональні до , а це неможливо. Пропозиція доведена.

Основні результати

Нехай - кінцева група, і - підгрупи групи . Будемо говорити, що група допускає факторізацію , якщо для всякого має місце рівність , де , . Факторізація називається максимальної, якщо й максимальні підгрупи в групі . Ми розглянемо максимальні факторізації симплектичної групи , певної над кінцевим полем .

Нехай і - цілі числа, , . Якщо - просте число, що ділить і не ділить числа для , то називають примітивним простим дільником числа .

Добре відомо, що при , і завжди є примітивний простий дільник числа . Нехай , де - просте число, - ціле позитивне число. Позначимо найбільший примітивний простий дільник числа (так, що ділить і не ділить для ). Визначимо як добуток всіх примітивних простих дільників . Ми будемо розглядати максимальні факторізації групи . Відзначимо, що

Теорема. 49Нехай , де - непарне число. Якщо , де й - максимальні підгрупи групи , тоді , де - максимальна параболічна підгрупа групи , ізоморфна й, яка має порядок