2020-05-21
78
Можно использовать формулу длины окружности: 
. Стало быть, отложим угол 
и получим точку 
.
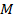Итак, расположение точки 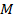найдено двумя способами.
Рис. 3.Нахождение декартовых координат точки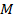
Найдем декартовы координаты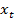 
и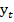 
. Эти координаты можно найти из прямоугольного треугольника 
. В нем известна гипотенуза 
, известен острый угол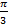 
(рис. 3). Значит, 
; 
.
Ответ: 
; 
.
Задача 2.
Дана точка 
; .
Найти: координаты точек 
, симметричных относительно осей координат и точке 
.
Решение:
Будет очевидным, если мы каждую дугу разделим на 3 равные части, каждая часть имеет длину 
, учтем симметрию и в результате получим ответ.
Для точки 
(рис. 4): 
; ; 
.
Для точки 
(рис. 4): 
; 
; 
.
Для точки 
(рис. 4): 
; 
; 
.
Рис. 4.Координаты симметричных точек относительно осей и относительно центра
Замечание
Криволинейных координат бесчисленное множество. Например, точка 
. Координата точки 
; 
; 
;
Обратная задача
Дано значение абсциссы 
.
Найти множество значений аргумента.
Множество значений всех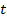 
. А именно, решить уравнение 
. Чтобы решить это уравнение, нужно вспомнить, каким образом по заданному числу 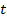мы получали точку 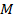и ее декартовы координаты. А именно, мы откладывали дугу, отмечали точку на окружности. Затем опускали перпендикуляры и получали декартовы координаты.
|
|
|
Здесь процесс выполняется в обратном направлении. Из точки 
(рис. 5) в координаты 
восстанавливаем перпендикуляр к оси 
и получим две точки 
и 
на единичной окружности. Это единственная пара точек на окружности с заданной абсциссой 
. Теперь нужно определить длину дуги 
(рис. 5). Рассмотрим треугольник 
. Гипотенуза – 1, катет – 
.
Рис. 5. Построение точки 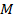и определение ее декартовых координат
Значит, 
. Отсюда 
. И соответствующая дуга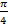 
. 
, значит, первая криволинейная координата точки 
: 
, а точки : 
.Все координаты точки 
, а все координаты точки 
(рис. 5).
Ответ: 
