2020-05-25
113Производная по направлению. Градиент.
Пусть функция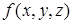 
дифференцируема в области 
и пусть в этой области задано некоторое направление 
. Производная функции 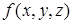по направлению 
вычисляется по формуле
(1)
Скорость наибольшего роста функции в данной точке (по величине и направлению) определяется вектором, который обозначается символом 
и называется градиентом функции:
(2)
Пример 1. Найти производную функции 
в точке 
в направлении 
. Чему равна величина градиента функции в этой точке?
Решение. Чтобы воспользоваться формулой (1), подсчитаем частные производные в точке 
:
Значит, производная функции в заданном направлении равна
.
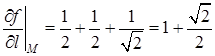В соответствии с формулой (2) запишем градиент функции в точке – вектор
Величина градиента (модуль вектора) равна 
. ☻
Пример 2. Найти производную функции 
в точке 
в направлении, составляющем угол 
с положительным направлением оси 
.
|
|
|
Решение. Подсчитаем сначала частные производные в точке :
.
Найдем направляющие косинусы:
.
По формуле (1) запишем
. ☻
Пример 3. Для функции 
определить угол между градиентами в точках 
и 
.
Решение. Подсчитаем сначала частные производные:
Теперь можем записать градиент функции в точках 
и 
:
,
.
Очевидно, эти векторы ортогональны – их скалярное произведение равно нулю: 
. Значит, угол между градиентами равен 
. ☻
Формула Тейлора для функций двух переменных
Если функция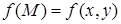 
имеет в некоторой окрестности точки 
непрерывные частные производные до (
) -го порядка включительно, то в этой окрестности справедлива формула
Здесь 
берется в точке
Остаточный член в форме Лагранжа имеет вид
,
, 
, 
, 
.
Остаточный член в форме Пеано (при более слабых предположениях).
, 
.
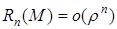Пример 4. Для функции 
записать формулу Тейлора в окрестности точки 
.
Решение. Подсчитаем 
. Найдем частные производные первого порядка:
Запишем первый дифференциал в точке :
.
Найдем вторые производные:
, 
, 
.
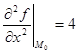Запишем второй дифференциал в точке :
.
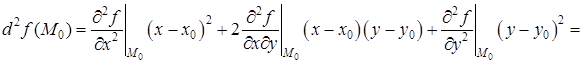
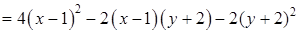Все производные порядка выше второго равны нулю. Формула Тейлора принимает вид
.
Фактически мы перегруппировали данный многочлен по степеням 
и 
. ☻
Пример 5. Записать формулу Тейлора 
-го порядка для функции 
в окрестности точки 
.
Решение. Находим 
. Подсчитаем частные производные первого порядка
.
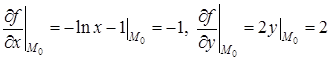Запишем первый дифференциал в точке :
.
Подсчитаем вторые производные:
, 
, 
.
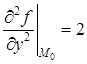Запишем второй дифференциал в точке :
.
Продолжаем дифференцировать: 
, все остальные производные 3-го порядка равны нулю.
|
|
|
Запишем третий дифференциал в точке : 
.
Легко заметить, что дальнейшее дифференцирование по 
приводит к формуле 
. Значит,
, 
.
Формула Тейлора принимает вид:
,
где 
, . ☻
В частном случае при 
получаем формулу Маклорена.
Пример 6. Функцию 
разложить по формуле Маклорена до членов второго порядка функцию .
Решение. Находим . Чтобы записать первый дифференциал, находим
.
Так как 
, то 
.
Чтобы записать второй дифференциал, находим
.
Так как 
, то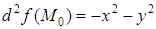 
.
Формула Маклорена принимает вид
, 
. ☻
