Практическая работа № 8
по теме: «Нахождение значений арксинуса, арккосинуса, арктангенса».
Пояснительная записка
Практическая работа предназначена для повторения теоретических и практических знаний по теме.
Цель работы – повторить понятия: тригонометрических функций, радианной меры углов, таблицы значений тригонометрических функций, формулы перевода градусов в радианы и наоборот, определения арксинуса, арккосинуса, арктангенса числа и подготовится к занятию по теме «Арксинус, арккосинус, арктангенс числа».
Данное пособие рекомендовано для студентов первого курса. Пособие содержит определения, свойства и формулы по теме: Арксинус, арккосинус, арктангенс числа, тест для самоконтроля.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Арксинус, арккосинус, арктангенс числа
Арксинус
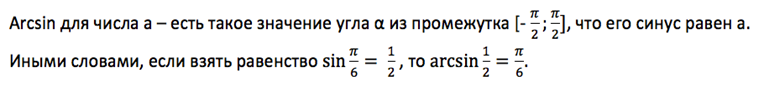
|
|
|
Чтобы больше понять о свойствах арксинуса, необходимо рассмотреть его функцию. График y = arcsin x имеет вид асимметричной кривой, проходящей через центр координат.
Свойства арксинуса:
1. 
2. Так как f(x) нечетная, то arcsin (- x) = — arcsin x.
3. Y = 0 при x = 0.
4. На всей своей протяженности график возрастает.
Если сопоставить графики sin и arcsin, у двух тригонометрических функций можно найти общие закономерности.

Арккосинус
Arccos числа а — это значение угла α, косинус которого равен а.
Кривая y = arcos x зеркально отображает график arcsin x, с той лишь разницей, что проходит через точку π/2 на оси OY.
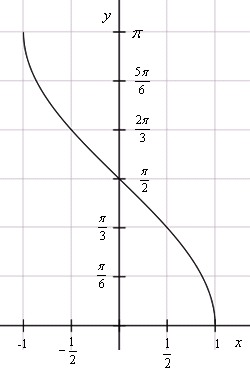
Рассмотрим функцию арккосинуса более подробно:
1. Функция определена на отрезке [-1; 1].
2. ОДЗ для arccos — [0, π].
3. График целиком расположен в I и II четвертях, а сама функция не является ни четной, ни нечетной.
4. Y = 0 при x = 1.
5. Кривая убывает на всей своей протяженности. Некоторые свойства арккосинуса совпадают с функцией косинуса.
Некоторые свойства арккосинуса совпадают с функцией косинуса.

Задание 1. Укажите функции изображенные на рисунке.
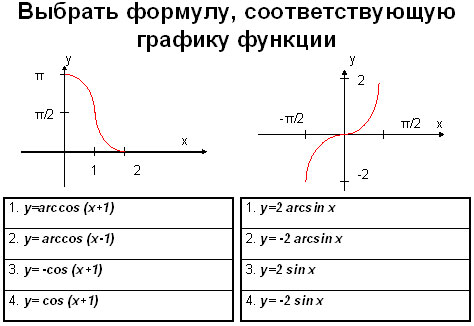
Ответ: рис. 1 – 4, рис.2 — 1.
Арктангенс
Arctg числа a – это такое значение угла α, что его тангенс равен а.
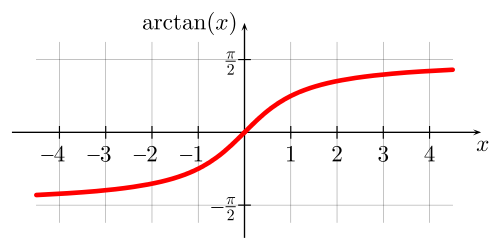
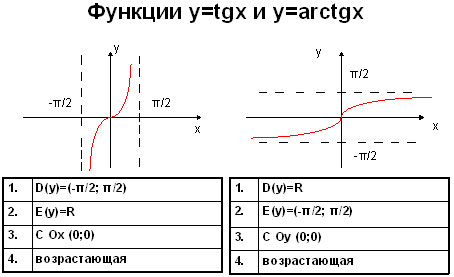
Если рассмотреть график арктангенса, можно выделить следующие свойства:
1. График бесконечен и определен на промежутке (- ∞; + ∞).
2. Арктангенс нечетная функция, следовательно, arctg (- x) = — arctg x.
3. Y = 0 при x = 0.
4. Кривая возрастает на всей области определения.

Приведем краткий сравнительный анализ tg x и arctg x в виде таблицы.
Арккотангенс
Arcctg числа a — принимает такое значение α из интервала (0; π), что его котангенс равен а.
|
|
|
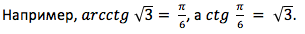

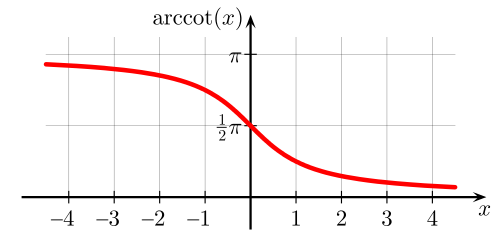
Свойства функции арккотангенса:
1. Интервал определения функции – бесконечность.
2. Область допустимых значений – промежуток (0; π).
3. F(x) не является ни четной, ни нечетной.
4. На всем своем протяжении график функции убывает.
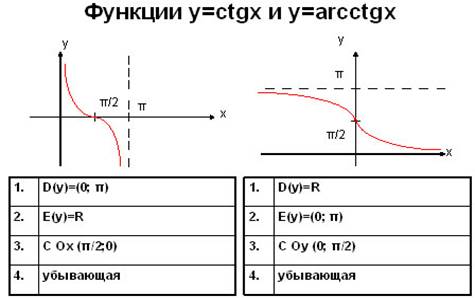
Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.
Задание 2. Соотнести график и форму записи функции.
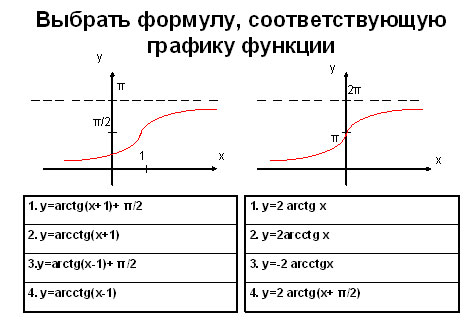
Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,
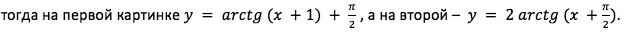
Ответ: рис. 1 – 1, рис. 2 – 4.
Пример 1. Вычислить значение 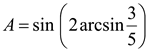 .
.
Решение. Если обозначить 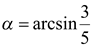 , то
, то 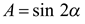 . Из определения функции
. Из определения функции 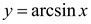 следует, что
следует, что 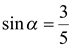 и
и 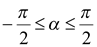 . Так как
. Так как 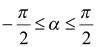 , то
, то 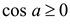 и
и 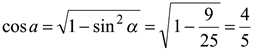 .
.
Однако 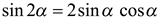 , поэтому
, поэтому 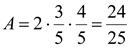 .
.
Ответ: 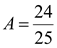 .
.
Пример 2. Вычислить значение 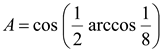 .
.
Решение. Если 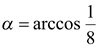 , то
, то 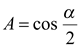 . Согласно определению функции
. Согласно определению функции 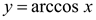 , имеем
, имеем 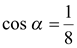 и
и 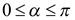 . Так как
. Так как 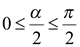 , то
, то 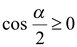 .
.
Поскольку 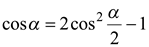 и
и 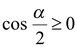 , то
, то 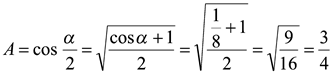 .
.
Ответ: 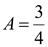 .
.
Пример 3. Вычислить значение 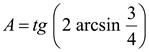 .
.
Решение. Пусть 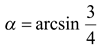 , тогда
, тогда 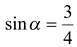 и
и 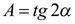 , где
, где 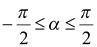 . В таком случае
. В таком случае 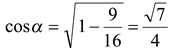 и
и 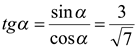 .
.
Поскольку 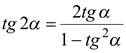 , то
, то 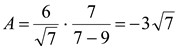 .
.
Ответ: 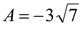 .
.
Пример 4. Вычислить значение 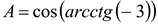 . Решение. Так как
. Решение. Так как 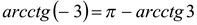 , то
, то 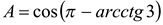 или
или 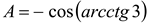 . Обозначим
. Обозначим 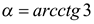 , тогда
, тогда 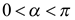 ,
, 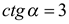
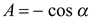 . Поскольку
. Поскольку 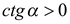 , то
, то 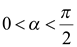 .
.
Если 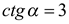 , то
, то 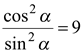 ,
, 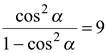 или
или 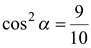 . Однако
. Однако 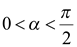 , поэтому
, поэтому 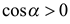 ,
, 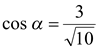 и
и 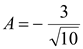 .
.
Ответ: 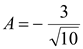 .
.
Пример 5. Вычислить значение 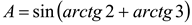 .
.
Решение. Если положить 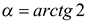 и
и 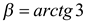 , то
, то 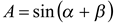 или
или
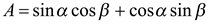 , (1)
, (1)
где из определения функции 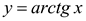 имеем
имеем 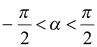 и
и 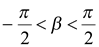 .
.
Однако 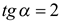 и
и 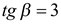 , поэтому
, поэтому 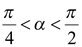 и
и 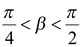 . В таком случае
. В таком случае 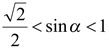 ,
, 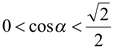 и
и 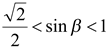 ,
, 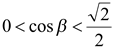 .
.
Если 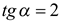 , то
, то 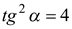 ,
, 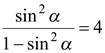 или
или 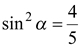 . Поскольку
. Поскольку 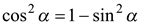 , то
, то 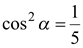 .
.
С учетом того, что 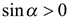 и
и 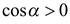 , имеем
, имеем 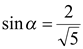 и
и 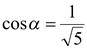 .
.
Если 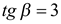 , то повторяя рассуждения, приведенные выше, получаем
, то повторяя рассуждения, приведенные выше, получаем 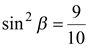 ,
, 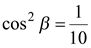 и
и 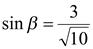 ,
, 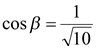 .
.
Подставляя значения 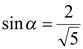 ,
, 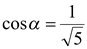 ,
, 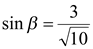 ,
, 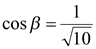 в выражение (1) получаем
в выражение (1) получаем 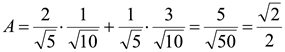 .
.
Ответ: 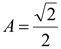 .
.
Примечание. Так как в примере 5 показано, что 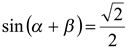 , где
, где 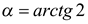 ,
, 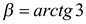 и
и 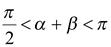 , то справедливо равенство
, то справедливо равенство
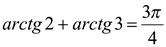 .
.
Отсюда также следует, что 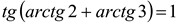 .
.
Пример 6. Вычислить значение 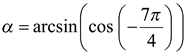 .
.
Решение. Из определения функции 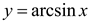 следует, что
следует, что 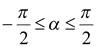 . Из условия примера получаем
. Из условия примера получаем 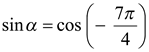 .
.
Так как 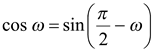 , то имеем уравнение
, то имеем уравнение 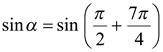 или
или 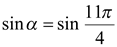 . Далее, принимая во внимание теорему 1, записываем две серии корней уравнения
. Далее, принимая во внимание теорему 1, записываем две серии корней уравнения 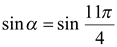 вида
вида
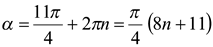 и
и 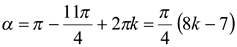 ,
,
где 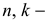 целые числа. Если положить
целые числа. Если положить 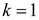 , то из второй серии корней вытекает единственное значение
, то из второй серии корней вытекает единственное значение 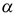 , которое удовлетворяет двойному неравенству
, которое удовлетворяет двойному неравенству 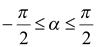 .
.
Ответ: 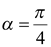 .
.
Пример 7. Вычислить значение 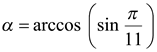 .
.
Решение. По определению функции 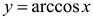 имеем
имеем 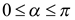 . Из условия следует, что
. Из условия следует, что 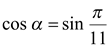 ,
, 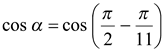 или
или
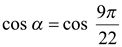 . (2)
. (2)
Согласно теореме 2, здесь имеем две серии корней уравнения (2):
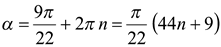 и
и 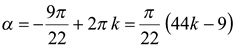 , где
, где 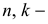 целые числа.
целые числа.
Так как 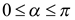 , то из первой серии корней при условии, что
, то из первой серии корней при условии, что 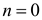 , получаем
, получаем 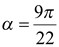 .
.
Ответ: 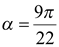 .
.
Тест по теме Арксинус, арккосинус, арктангенс числа
Найдите значение выражения:
1. аrcsin (- 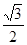 )
)
а)  ; б)
; б) 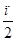 ; в) -
; в) - 
2. arcos (- 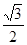 )
)
а) -  ; б)
; б)  ; в)
; в) 
3. arctg 
а)  ; б) -
; б) -  ; в) 1
; в) 1
4. arctg 1 + arcos 1
а)  ; б) 0; в)
; б) 0; в) 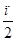
5. аrcsin (- 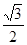 ) + arcos (-
) + arcos (- 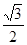 )
)
а) 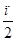 ; б)
; б)  ; в) -
; в) - 
6. cos (arcos 
а)  ; б) -
; б) -  ; в) 1
; в) 1
7. arcos (cos  )
)
а)  ; б)
; б)  ; в) -
; в) - 
 2020-06-30
2020-06-30 1443
1443







