2020-08-05
242
Одночлен или моном – простое математическое выражение, прежде всего рассматриваемое и используемое в элементарной алгебре, а именно, произведение, состоящие из числового множителя и одной или нескольких переменных, взятых каждая в неотрицательной степени. Одночленом также является каждое отдельное число, причем степень такого одночлена равна нулю.
Многочлен или полином от n переменных от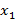 
до 
– сумма одночленов или строго конечная сумма следующего вида, в котором 
– набор из n целых чисел, именуемый мультииндексом; 
– число, именуемое коэффициентом многочлена, зависящее только от мутииндекса I.
С помощью многочлена вводятся понятия «алгебраическое уравнение» и «алгебраическая функция».
Полной степенью одночлена называется целое число следующего вида
Множество мультииндексов I, для которых коэффициенты ненулевые, называется носителем многочлена, а его выпуклая оболочка – многогранником Ньютона. Степенью многочлена называется максимальная из степеней его одночленов.
Коэффициенты многочлена обычно берутся из определенного коммутативного кольца R. Иными словами, для операций сложения и умножения многочлены образуют кольцо, которое обозначается 
. Сложение и вычитание многочленов происходит по следующему принципу:
1. Составляется сумма или разность исходных многочленов, для чего многочлены заключаются в скобки и между этими скобками ставятся знаки сложения или вычитания;
2. Скобки раскрываются;
3. Приведение к стандартному виду (приведение подобных).
Умножение многочлена на многочлен базируется на распределительном свойстве умножения и сводит умножение многочленов к умножению друг на друга всех составляющих их членов – умножению одночленов. Чтобы умножить на каждый член второго многочлена и сложить полученные произведения.
На основании умножения многочленов вводится действие возведения многочлена в степень, которое заключается в умножении многочлена на само себя столько раз, сколько указывает показатель степени.
Деление многочлена на многочлен существенно отличается от всех вышеуказанных действий и в общем случае результатом выполнения действия не является многочленом. В частных случаях результатом деления двух многочленов является многочлен. Многочлен 
делится без остатка на многочлен 
, если существует многочлен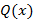 
такой, что справедливо следующее соотношение 
.
Теорема: Любой многочлен степени 
можно представить в виде
, где 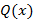– некоторый многочлен степени 
; – многочлен степени 
и 
– многочлен, степень которого меньше k, причем такое представление единственно.
Деление многочлена на многочлен удобно выполнять уголком по аналогии с обычными действительными числами.
Пусть A – алгебра над кольцом R, тогда произвольный многочлен
определяет полиномиальную функцию 
. В случае, если R – поле вещественных или комплексных чисел, тогда функция 
полностью определит многочлен p. В общем случае это неверно. Полиномиальная функция одного действительного переменного называется целой рациональной функцией.
