Затухающие колебания

 

 

1. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии ко­лебательной системой.

Свободные колебания реальных систем всегда затухают. Затухание свободных ме­ханических колебаний вызывается главным образом трением, сопротивлением окружа­ющей среды и возбуждением в ней упругих волн. Затухание в электрических колеба­тельных системах вызывается тепловыми потерями в проводниках, образующих сис­тему или находящихся в ее переменном электрическом поле, потерями энергии на излучение электромагнитных волн, а также тепловыми потерями в диэлектриках и фер­ромагнетиках вследствие электрического и магнитного гистерезиса.

Закон затухания колебаний зависит от свойств колебательной системы.

Система называется линейной, если па­раметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса.

Линейные системы описываются линей­ными дифференциальными уравнениями. Например, пружинный маятник, движущий­ся в вязкой среде, представляет собой ли­нейную систему, если коэффициент сопро­тивления среды и упругость пружины не зависят от скорости и смещения маятника. Электрический колебательный контур мож­но считать линейной системой, если его электрическое сопротивление R, электроем­кость С и индуктивность L не зависят ни от тока в контуре, ни от напряжения. В боль­шинстве случаев реальные колебательные системы достаточно близки по своим свой­ствам к линейным.

2. Найдем дифференциальное уравнение, описывающее свободные затухающие коле­бания линейной системы. Для этого рас­смотрим два примера линейных систем — механической и электрической, колебания которых сопровождаются диссипацией энергии.

 

Пример 1. Свободные затухающие колебания пружинного маятника массы m, движущегося в вязкой среде вдоль оси ОХ. На маятник дей­ствуют две силы: сила упругости пружины F_упр и сила сопротивления среды F_c, которую, как показывает опыт, можно считать в первом при­ближении пропорциональной скорости маятни­ка v и направленной в противоположную v сто­рону: F_c= — bv, где b — постоянный положитель­ный коэффициент пропорциональности, называе­мый коэффициентом сопротивления. По второму закону Ньютона, дифференциальное уравнение движения маятника имеет вид

                            

 

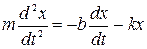
или                                           (28.1)

где 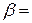b/(2m),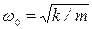

 

Пример 2. Свободные затухающие колебания в электрическом колебательном контуре. Электри­ческое сопротивление реального контура R≠0, и, согласно (27.22), колебания заряда конденсатора описываются уравнением

 

 

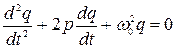                                                                (28.2)

где

               

 

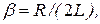
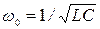
Уравнения (28.1) и (28.2) тождествен­ны по форме. Поэтому можно утверждать, что общее дифференциальное уравнение свободных затухающих колебаний рассмот­ренных линейных систем имеет вид

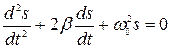                               (28.3)                                                            

Здесь s — изменяющаяся при колебаниях физическая характеристика системы; 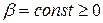 — коэффициент затухания;ω ₀ — циклическая частота свободных неза­тухающих колебаний той же системы, т. е. в отсутствие потерь энергии (при ).

 

 

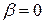4. Затухающие колебания не явля­ются периодическими, так как максимальное значение колеблющейся величины s, достигаемое в некоторый момент време­ни t₁, в последующем (при t>t₁) никогда не повторяется. Однако при затухающих колебаниях величина s обращается в нуль, изменяясь нa одну и ту же сторону (например, убывая), а также достигает макси­мальных и минимальных значений через равные промежутки времени:

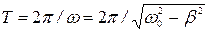                               (28.10)

Величины Т и ω поэтому обычно называ­ют периодом (условным периодом) и цикли­ческой частотой (условной циклической частотой) затухающих колебаний.

 

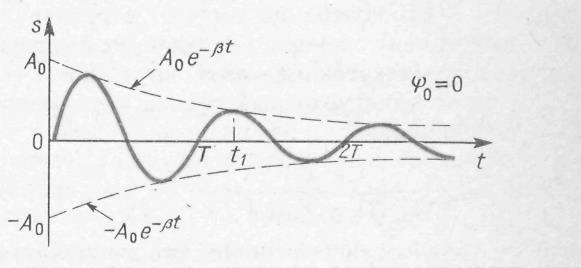
Величина

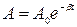
                                             (28.11)                                                                                                                                                                                                                                                                             

называется амплитудой затухающих коле­баний, соответственно A₀— начальной ам­плитудой. Амплитуда затухающих колеба­ний уменьшается с течением времени и тем быстрее, чем больше коэффициент затуха­ния .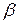

Промежуток времени t, в течение кото­рого амплитуда затухающих колебаний уменьшается в e раз, называется временем релаксации:

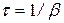
Для количественной характеристики быстроты убывания амплитуды затухающих колебаний пользуются понятием логариф­мического декремента затухания.

Логарифмическим декрементом затуха­ния называется безразмерная величина 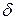, равная натуральному логарифму отноше­ния значений амплитуды затухающих коле­баний в моменты времени t и t+T (T- условный период колебаний):

                                                 (20.12)

 

где N — число колебаний, в течение кото­рых амплитуда уменьшается в е раз.,

Найдем связь между циклической часто­той 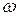  затухающих колебаний системы и ло­гарифмическим декрементом затухания .

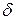Так как

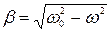и T=2 / ,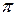

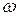то 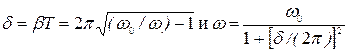                                      (28.13)

Вынужденные механические колебания

1. Переменная внешняя сила, приложен­ная к системе и вызывающая ее вынужден­ные механические колебания, называется вынуждающей, или возмущающей силой.

Дифференциальное уравнение вынуж­денных колебаний простейшей линейной системы— пружинного маятника, происхо­дящих вдоль оси ОХ под влиянием пере­менной внешней силы F (t), отличается от (28.1) только правой частью, равной отно­шению F_x (t) к массе маятника m

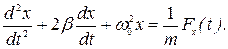                              (28.18)

Если F_x (t) — периодическая функция времени, то после приложения этой силы к маятнику вначале возникает переходный режим вынужденных колебаний, при кото­ром маятник одновременно участвует в двух колебаниях:

x (t)=x₁(t)+x₂(t)                                                              (28.19)

Первый член соответствует свобод­ным затухающим колебаниям маятника (28.9) ¹⁾:

 

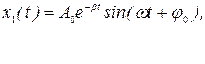
где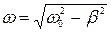                                           

Второй член соответствует незатухаю­щим периодическим колебаниям маятника с частотой, равной частоте возмущающей силы F_x (t).

Амплитудное значение х₁ (t), равное A₀^βt, более или менее быстро уменьшается после начала вынужденных колебаний: за время τ₀ =4,6/β амплитуда х₁ (t) умень­шается в 100 раз. Следовательно, через некоторое время т после начала колебаний свободные колебания маятника практически прекращаются: х (t) 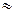x₂ (t). Маятник переходит в состояние установив­шихся вынужденных колебаний, совершаю­щихся с частотой возмущающей силы.

2. Рассмотрим вынужденные колебания пружинного маятника, происходящие под действием возмущающей силы, которая из­меняется по гармоническому закону с цик­лической частотой Ω:

F_x=F₀cosΩt                                                                                        (28.20)

где F₀ - амплитуда возмущающей силы.

Покажем, что установившиеся вынуж­денные колебания маятника будут тоже гармоническими с той же частотой, т. е. найдем такие значения А и φ₀, чтобы выражение

х=А cos (Ωt + φ₀)                                                                         (28.21)                                                                                                                                                                                                                   обращало уравнение (28.18) в тождество. Из (28.21) следует,

dx/dt=-AΩ sin(Ωt + φ₀)=AΩcos (Ωt + φ₀ +π/2).

d²x/dt² =-AΩ² cos (Ωt + φ₀)= AΩ² (Ωt + φ₀ +π).                     (28.22) 

Подставим (28.21) и (28.22) в (28.18):

А₁ cos (Ωt + φ₀ +π)+ A₂ cos (Ωt + φ₀ +π/2)+ 

+A₃ cos (Ωt + φ₀)=B cos Ωt.                                                          (28.23)

Здесь использованы следующие сокращенные обозначения:

А₁ = Ω² А, А₂ =2βΩА, А₃ =ω₀² А, В=F₀ /m.                        (28.24)                                                                                                                                                                                                                                              

Уравнение (28.23) показывает, что сумма трех одинаково направленных гармоничеcких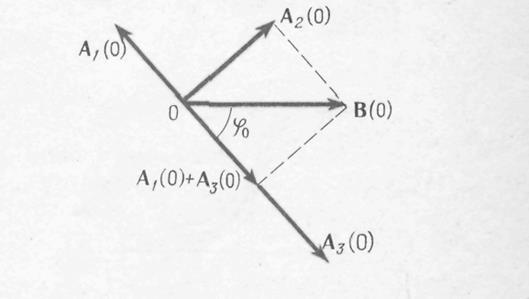

колебаний с амплитудами А₁, А₂, Аз, одинаковой циклической частотой Ωи раз­личными начальными фазами (φ₀ +π), (φ₀ +π/2) должна совпадать с гармониче­ским колебанием, происходящим но закону В cosΩ t. Для сложения этих трех колеба­ний мы воспользуемся методом векторных диаграмм. На рис. 28.3 изображены векто­ры амплитуд всех четырех колебаний в начальный момент времени А₁(0), А₂(0), Аз(0) и В(0). Эти векторы должны удовлет­ворять условию (28.23), т.е.

A₁ (0)+А₂ (0)+А₃(0)=В (0).  (28.24')

Из рис. 28.3 и формул (28.24') следует, что амплитуда А установившихся вынужден­ных колебаний и сдвиг фаз φ₀

 

 

 

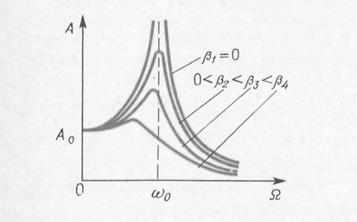
между смешением маятника из положения равно­весия и вынуждающей силой зависят от соотношения между циклическими часто­тами вынужденных колебаний Ωи свобод­ных незатухающих колебаний ω₀, а также от коэффициента затухания β:

    

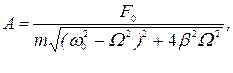
  tgφ₀ = -2βΩ/(ω₀² – Ω²).                                        (28.25)

 

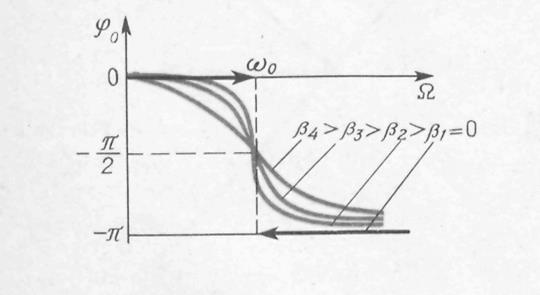
При Ω = 0 получим φ₀(0)=0 и А(0)=A₀= F₀/(mω²)=F₀ /k - статическое сме­шение маятника из положения равновесия под действием постоянной силы F_x=Fo. При Ω 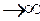 амплитуда А (Ω)  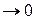и tg φ₀ 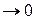, а φ₀ . Графики зависимости A (Ω) и φ₀ (Ω) при различных значениях коэффи­циента затухания β показаны на рис. 28.4 и 28.5.

 

 

Сложением колебаний

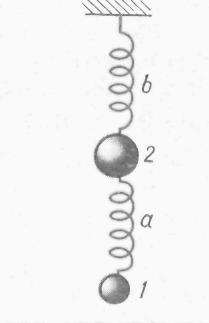
1. Под сложением колебанийпонимают нахождение закона результирующих коле­баний системы в тех случаях, когда эта система одновременно участвуете несколь­ких колебательных процессах. Различают два предельных случая: сложение колеба­ний одинакового направления и сложение взаимно перпендикулярных колебаний. Первый случай соответствует, например, колебаниям грузика 1 (рис. 27.7), который колеблется относительно грузика 2 на пру­жине а и вместе с ним на пружине b. Этот же случай реализуется при наложении ко­лебаний скалярных физических характери­стик колебательной системы (давления, температуры, плотности, тока и т. п.).

2 Сложение двух одинаково направлен­ных гармонических колебаний

                                        s₁ = A₁ sin(ωt+φ₁)

                                         s₂ = A₂₁ sin(ωt+φ₂)

можно произвести, воспользовавшись мето­дом векторных диаграмм. На рис. 27.8 по­казаны векторы А₁(t) и А₂ (t) амплитуд первого и второго колебаний в произвольный момент времени t, когда фазы этих колебаний равны Ф₁ (t) = ω₁t+ф₁ и Ф₂ (t) =ω₂t + φ₂. Результирующим колебаниям s = s₁ +s₂ соответствует вектор А(t)= A₁ (t) + А₂(t), проекция которого на ось ОК

s = A (t) sin Ф (t).                                                     (27.30)

 

                                                                                                                                                                                                         

По теореме косинусов,

[A(t)]²=A₁²+A₂²+2A₁A₂cos[Φ₂(t)-Φ(t)]                                  (27.30')

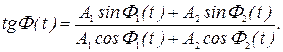
Два колебательных процесса называют­ся когерентными колебаниями, если они со­гласованно протекают во времени, так что разность их фаз остается постоянной.

Разность фаз двух гармонических колебаний s₁  и s₂ равна

Φ₂ (t) = Φ₁ (t)=(ω₂ –ω₁) t+(φ ₂ - φ ₁)

Следовательно, два гармонических ко­лебания когерентны, если их циклические частоты одинаковы, т. е.любой момент времени разность фаз когерент­ных гармонических колебаний равна разно­сти их начальных фаз: Ф₂ (t)—Ф₁ (t)=(ω₂-ω₁)t+(φ₂ – φ₁).

Соответственно результирующие колебания — гармонические с той же циклической частотой ω, т. е.

s= s₁+ s₂ =Аsin (ωt+φ₀),                                          (27.31)                                                                                                        

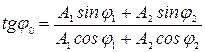                                                              (27.31^')                                                                                                   

В зависимости от разности начальных фаз складываемых колебаний амплиту­да А результирующих колебаний изменяет­ся в пределах

от А=|А₁—А₂|

при φ₂ –φ₁= ± (2m+1)π

до А=А₁+ А₂ при φ₂ – φ₁=± 2m π

где где m=0,1,2…— любое целое неотрица­тельное число. Если φ₂ – φ₁=±2mπ, то колебания синфазны(находятся в одной фазе), а если φ₂ –φ₁= ± (2m+1)π

то находятся в противофазе.

 

9. Сложение взаимно перпендикулярных колебаний с циклическими частотами рω и q ω, где p,q— целые числа:

х =A₁ sin (p ωt+ φ₁), у=А₂ sin (q ωt+ φ₂).                                  (27.43)

Значения координат х u у колеблющейся точки М одновременно повторяются через одинаковые промежутки времени T₀, равные общему наименьшему кратному Т₁ = 2π/(pω) и T₂ = 2π(qω) —периодов ко­лебаний вдоль осей ОХ и OY. Поэтому тра­ектория точки М — замкнутая кривая, форма которой зависит от соотношения ам­плитуд, частот и начальных фаз складывае­мых колебаний. Такие замкнутые траектории точки М, одновременно совершающей гар­монические колебания в двух взаимно

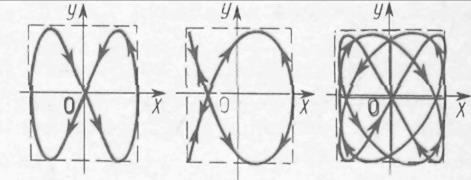       перпендикулярных направлениях, называются фигурами Лиссажу. Фигуры Лиссажу впи­сываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат ОХ и OY и расположены по обе стороны от них на расстояниях, соответственно равных A₂ и A₁.Отношение частот рω и qω складывае­мых колебаний равно отношению числа ка­саний соответствующей им фигуры Лисса­жу со стороной прямоугольника, параллель­ной оси OY, и со стороной, параллельной оси ОХ. На рис. 27.12 показан вид фигур Лиссажу при трех различных значениях отношения q/p (2:1, 3:2, 4:3) и разности начальных фаз ∆ φ =φ₁ – φ₂=π/2.              

Вопросы:

1.Что изменится в уравнении гармонических колебаний, если в векторной диаграмме вра­щать вектор амплитуды по направлению часо­вой стрелки?

2.От чего зависят амплитуда и начальная фаза гармонических механических колебаний?

3. Можно ли с помощью векторной диаграммы найти результат сложения трех одинаково направленных гармонических колебаний од­ной частоты?

4. Как получить эллиптически поляризованные колебания?

5. Как по виду фигуры Лиссажу найти отношение частот складываемых колебаний? В каких слу­чаях это можно сделать?

6. Что понимают под спектром колебаний?

 

Упругая волна

называется продольной, если частицы среды колеблются в направле­нии распространения волны.

Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде — твердой, жидкой и газообразной. Примером таких волн являются звуковые волны в воздухе.

Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направле­нию распространения волны.

Поперечные волны связаны с деформа­цией сдвига упругой среды и, следователь­но, могут образовываться и распростра­няться только в средах, обладающих упру­гостью формы, т. е. в твердых телах. Примером поперечных волн могут служить волны, распространяющиеся вдоль струн музыкальных инструментов.

Особое место занимают поверхностные волны - распространяющиеся вдоль сво­бодной поверхности жидкости (или повер­хности раздела двух несмешивающихся жидкостей) возмущения этой поверхности, возникающие под влиянием внешних воз­действий (падения тел, движения судов, ветра и т. п.). В образовании и распростра­нении этих волн определяющую роль играют силы поверхностного натяжения и тяжести. В поверхностных волнах частицы жидкости одновременно совершают поперечные и про­дольные колебания, описывая эллиптиче­ские или более сложные траектории.

Среда называется однородной, если ее физические свойства, существенные в рас­сматриваемых задачах, не изменяются от точки к точке.

§ 29.2.

 1. Уравнением упругой волны называется зависимость от координат и времени ска­лярных или векторных величин, характери­зующих колебания среды при прохождении в ней рассматриваемой волны.

Например, для волн в твердой среде такой величиной может служить вектор сме­щения частицы среды из положения равно­весия или три его проекции на оси коорди­нат. Для характеристики продольных волн в газе или жидкости обычно пользуются из­быточным давлением колеблющейся среды, равным разности между ее переменным и равновесным давлениями.

Распространение в упругой среде меха­нических возмущений, возбуждаемых ис­точником волн, связано с переносом волна­ми энергии. Поэтому такие волны в отличие от стоячих волн (см. § 29.6) называют бе­гущими волнами.

Линия, касательная к которой в каждой ее точке совпадает с направлением распро­странения волны, т. е. с направлением пе­реноса энергии волной, называется лучом.

В однородной среде лучи имеют вид прямых линий.

 

5. Уравнение плоской синусоидальной вол­ны, распространяющейся в непоглощающей среде вдоль положительного направле­ния оси ОХ,

    s=A sin [ω(t - x/v) + φ₀]=

    А sin (ωt - ωx/v + φ₀),                                                                          (29.4)

или

s = A sin [2πt/T -2πx/ (Tv) + φ₀]                                                               (29.4')

где A=const — амплитуда колебаний, на­зываемая амплитудой волны;

ω = 2л/Т — циклическая (круговая) частота волны;

Т — период колебаний; φ₀— начальная фа­за колебаний в точках координатной плос­кости х = 0. Величина Ф =ωt - ωt/v + φ₀равная фазе колебаний в произвольной точ­ке с координатой х, называется фазой плос­кой волны.

Расстояние λ=vТ, на которое распро­страняется синусоидальная волна за время, равное периоду колебаний, называется дли­ной волны.

Длина волны равна расстоянию между двумя ближайшими точками среды, в кото­рых разность фаз колебаний равна 2π.

6. Наряду с длиной волны используется другая характеристика синусоидальной вол­ны — волновое число, которое показыва­ет, сколько длин волн укладывается на от­резке длиной 2 π:

     k=2 π / λ = 2 π / (vT) =ω/v.                                                       (29.5)                                                                                                                                   

Следовательно, уравнение плоской си­нусоидальной волны (29.4) можно также представить в виде

       s = A sin (ωt-2 πx/ λ +φ₀)= A sin (ωt- k x +φ₀).                      (29.6)

 

Соответственно фаза этой плоской волны

        Ф =ωt - ωt/v + φ₀.

Волновым вектором называется век­тор к, по модулю равный волновому числу k и направленный вдоль луча в рассмат­риваемой точке М среды,

Волновой вектор плоской синусоидаль­ной волны не зависит от выбора точ­ки М. Для плоской волны, распространяю­щейся вдоль положительного направления оси OX, k — k i (i — орт оси ОХ), поэтому kх =kг, где г — радиус-вектор точки М, и уравнение плоской волны (29.6) можно за­писать в форме

          s = A sin ( ω t— kr + φ₀).                                                             (29.7)                                                                                                                                                                     

Основываясь на формуле (27.5), урав­нение волны (29,7) можно записать в экспо­ненциальной форме, удобной для диффе­ренцирования:

s = Ae^{i(ωt— kr + δ)}                                                              (29.7')                                                                                                                                                                                                    

где i = 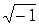и δ = φ₀—π/2.

Физический смысл имеет только действительная часть комплексной величины š, т. е. величина s = Reš. Пользуясь š для нахождения ка­кой-либо характеристики волны, нужно по­сле выполнения всех математических операций отбросить мнимую часть полученного комплексного выражения.

 

 

  29.3.

1. Найдем выражение для скорости и про­дольной волны в однородной газообразной среде. Пусть газ находится в длинном гори­зонтальном цилиндрическом сосуде с под­вижным поршнем площадью s. Первона­чально поршень находился в покое, а в мо­мент времени t пришел в движение и за малый промежуток времени dt приобрел скорость dv₁, сместившись при этом на рас­стояние dv₁, dt/2. Возмущающее действие поршня за время dt распространится в газе на расстояние v dt и охватит область среды объемом Sv dt, относительная объемная де­формация которой

             dε= 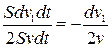                                     (29.12)

 

 

Добавочное давление dp, производимое на газ движущимся поршнем, можно найти из закона Гука (29.1), где (DV/V) = dε:

       dp = 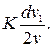                                                           (29.13)

 

Под действием силы dF = S dp возмущен­ный поршнем газ приобретает за время dt импульс, равный dm dv₁/2, где dm =ρSv dt, ρ — плотность газа. По второму закону Ньютона,

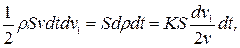
откуда искомая скорость продольной волны в газе

     v= 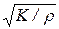                                                             (29.14)

 

Заметим, что при выводе формулы (29.14) предполагалось, что плотность газа  ρ —const. В газах это условие соблюда­ется, если избыточное давление, связанное с распространением волны, во много раз меньше равновесного давления невозму­щенного газа.

Формула (29.14) справедлива также для продольных волн в жидкостях.

 

 

29.4

|1.Упругая среда, в которой распространя­ются механические волны, обладает как кинетической энергией колебательного дви­жения частиц, так и потенциальной энер­гией, обусловленной деформацией. Если v₁—скорость колебаний частиц среды, то объемная плотность кинетической энергии среды

 w_k = 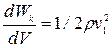                                              (29.21)

 

где ρ — плотность среды; dW_K— кинетиче­ская энергия всех частиц в малом объеме dV среды, выбранном таким обра­зом, что в его пределах скорость v₁\ всюду одинакова.

Можно доказать, что объемная плот­ность потенциальной энергии упругодеформированной среды

 w_n =                                              (29.22)

               

где dW_n — потенциальная энергия однород­но деформированного малого участка среды объемом dV; v —фазовая скорость волны в среде; ε — относительная деформация.

Покажем справедливость формулы (29.22) на примере продольной волны в га­зе. Элементарная работа, совершаемая внешними силами давления при объемной деформации, δ A' = — р dV. По закону Гука (29.1),

δ A'=-pdv=(V/K)pdρ.

Эта работа идет на увеличение потенциаль­ной энергии упругодеформированной среды:

dW_n = δ A'=(V/K) ρdp.

Соответственно при конечной относительной деформации среды ε =ΔV/V

W_n=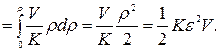

где в соответствии с законом Гука (29.1] ρ= —Кε. Следовательно, объемная плот­ность потенциальной энергии среды

W_n=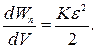

Если учесть, что, согласно (29.12), К=ρv², то это выражение можно переписать в форме (29.22).

Под объемной плотностью энергии упру­гих волн понимают объемную плотность w механической энергии среды, обусловлен­ную распространением этих волн и равную сумме w_к и w _п:

w= w_к + w_n = 1/2 ρ(v₁²+v²ε²)                                       (29.23)

 

3. Скорость переноса энергии волной рав­на скорости перемещения в пространстве поверхности, соответствующей максималь­ному значению объемной плотности w энер­гии волны. Для синусоидальных волн эта скорость равна фазовой скорости v.

Потоком энергии dФ_w сквозь малую пло­щадку dS называется отношение энер­гии dW, передаваемой через эту площадку за малый промежуток времени, к его дли­тельности dt:

         dФ_w = dW/ dt                                             (29.27)

Если v — вектор скорости переноса энергии волной, то dW равно энергии, за­ключенной внутри показанного на рис. 29.2 косого цилиндра с основанием площадью dS и образующей длиной vdt:

dW = wv dt dS cos α = w (v dS) dt,             

                                                                                (29.28)

dФ_w= w (vdS) = (UdS),

где w — объемная плотность энергии вол­ны; dS = n dS — вектор площадки dS; n — единичный вектор нормали к площад­ке; а — угол между v и dS.

Вектор плотности потока энергии

  U = wv.                                                                 (29.29)                                                                                                                                                                                                                                                                                                                                  

называется вектором Умова, так как впер­вые был введен Н. А. Умовым (1874). Век­тор направлен в сторону переноса энергии волной, а по модулю равен отношению пото­ка энергии dФ_w сквозь малую площадку dS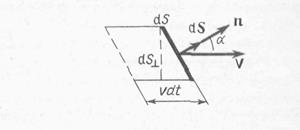

к площади dS_┴ — dS cosα   проекции этой площадки на плоскость, перпендикулярную направлению переноса энергии:

          U= dФ_w / dS_┴                                                            (29.29')                                                                                                                                                                                                                                

Поток энергии через произвольную по­верхность S, мысленно проведенную в сре­де, охваченной волновым движением, равен потоку вектора Умова через эту поверх­ность:

  Ф_w= 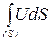                                                             (29.30)

29.5

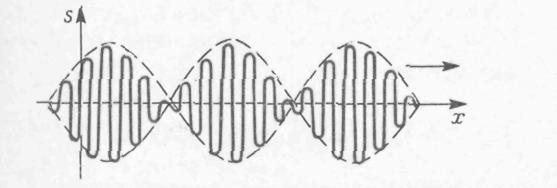
 3. Простейшей группой волн является ква­зисинусоидальная плоская волна, получаю­щаяся в результате наложения двух рас­пространяющихся вдоль оси ОХ плоских волн с одинаковыми амплитудами и близки­ми по значению частотами и волновыми числами:

s = A₀ sin (ωt – kx)+A₀sin [(ω +d ω)t – (k+dk)x] =

= 2A₀cos[(tdω – xdk)/2]sin(ωt-kx)                                       (29.36)

 

Зависимость s (x) в некоторый фиксиро­ванный момент времени t показана на рис. 29.4. Эта волна отличается от синусои­дальной тем, что ее амплитуда

A = 2A₀‌‌‌‌│‌cos [(tdω – xdk)/2] ‌│                                      (29.37)

— медленно изменяющаяся функция коор­динаты х и времени t.

За скорость распространения этой неси­нусоидальной волны принимают скорость и перемещения точки М, в которой амплиту­да А имеет какое-либо фиксированное зна­чение (например, A=0 или A = 2Aо). Сле­довательно, точка М движется по закону  tdω -  xdk = const, откуда                                                                                                                                                                                                                                                                                                      

u = 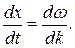                                                                       (29.38)

 

 

Величина и называется групповой ско­ростью. Она равна скорости переноса

энергии квазисинусоидальной волной. Группо­вая скорость u = d/dk пригодна для опи­сания переноса энергии (передачи сигнала) посредством несинусоидальных волн, имею­щих иной спектр частот, при условии, что спектр не очень широк, а дисперсия волн в среде для этих частот мала.

Найдем связь между групповой и фазо­вой скоростями волны. Так как t

ω= vk, a k = 2π/λ и dk=—2πdλ/λ², где λ — длина волны, то

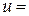
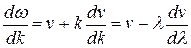                                                     (29.38)

§ 29.6.

5. Частным случаем интерференции волн являются стоячие волны.

Стоячей волной называется волна, об­разующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, в случае поперечных волн еще и одинако­вую поляризацию (§ 29.2).

Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приво­дится в колебательное движение.

При наложении двух когерентных бегу­щих плоских волн вида

            s₁= Asin (ωt — kx),

            s₂ = A sin (ωt + kx+α)

где α — разность фаз волн в точках плоско­сти x = O, образуется плоская синусоидаль­ная стоячая волна, описываемая уравнением

       s = s₁+ s₂=2A cos(kx + α/2)sin(ωt+ α/2)                                      (29.47)

Амплитуда стоячей волны A_ст в отличие от амплитуды А бегущих волн является периодической функцией координаты х:

        A_cn = 2A‌│cos (kx+ α/2) ‌│.  

Точки, в которых амплитуда стоячей волны A_ст = 0, называются узлами стоячей волны, а точки, в которых амплитуда A_ст максимальна  (A_ст =2А), называются пуч­ностями стоячей волны.

Положение узлов и пучностей находится из условий

               kx +α/2=(2m+1) π/2(узлы)

                                                                                                    (29.49)

                kx +α/2=mπ (пучности),                

 

где m = 0, 1, 2.....Расстояния между двумя соседними узлами и между двумя соседни­ми пучностями одинаковы и равны половине длины волны бегущих волн. Эту величину называют длиной стоячей волны: λ_ст = λ/2. Расстояние между соседними узлом и пуч­ностью стоячей волны равно λ_ст /2.

 

7. В стоячей волне (29.47) скорость коле­бательного движения частиц среды

 

v₁ =ds/dt = 2Аω cos (kx-\-a/2) cos (ωt +a/2),        (29.50)

 

а относительная деформация среды

ε=ds/dx= -2Ak sin (kx+a/2)  sin (ωt +a/2)=

2Ak sin (kx+a/2) cos(ωt +a/2+π/2)                                                   (29.51)

Таким образом, в отличие от бегущей волны, для которой справедливо соотноше­ние (29.24), в стоячей волне ε опережает v₁ по фазе на л/2, так что в те моменты време­ни, когда v_t достигает амплитудного значе­ния, ε обращается в нуль, и наоборот. Кроме того, амплитуды v₁ и ε зависят от координа­ты х и притом различным образом:

в пучностях стоячей волны располагаются пучности скорости частиц и узлы деформа­ции среды, а в узлах стоячей волны — пучности деформации и узлы скорости.

В упругой стоячей волне энергия перио­дически преобразуется из потенциальной энергии, локализованной в основном вблизи пучностей деформации, в кинетическую, ло­кализованную в основном вблизи пучностей скорости, и обратно. Поэтому энергия пери­одически мигрирует от узлов стоячей волны к се пучностям и обратно. Однако в самих узлах и пучностях плотность потока энергии тождественно равна нулю. Среднее за пери­од значение плотности потока энергии рав­но нулю в любой точке стоячей волны, так как две бегущие волны, образующие стоя­чую, переносят за период равную энергию в прямо противоположных направлениях. Именно поэтому стоячие волны и получили свое название.

Вопросы:

 1. Возможно ли образование сходящейся сфе­рической волны?

2. Что понимается под уравнением волны и под волновым уравнением?

3. От чего зависит фазовая скорость волн в уп­ругой среде?

&. Каковы должны быть свойства среды, чтобы для механических волн в этой среде выпол­нялся принцип суперпозиции?

5. Как связаны между собой амплитуда синусои­дальной волны в упругой среде и объемная плотность энергии этой волны?

6. Каков физический смысл групповой скорости?

7. Чем принципиально отличается бегущая волна, от стоячей? Чему равен вектор Умова в узлах и пучностях стоячей волны? Чему равна интен­сивность стоячей волны?