Практическая часть
Пример 3. При увеличении напряжения может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов; вероятности отказа элементов соответственно равны 0,2; 0,3; 0,4. Определить вероятность того, что разрыва цепи не произойдет.
Решение. Пусть события А1, А2, А3 означают выход из строя соответственно первого, второго и третьего элементов. Их вероятности по условию соответственно равны: P(A1)=0,2; P(A2)=0,3; P(A3)=0,4. Тогда вероятности противоположных событий 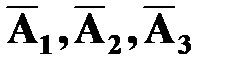 (соответственно первый, второй и третий элемент не вышел из строя) равны:
(соответственно первый, второй и третий элемент не вышел из строя) равны:
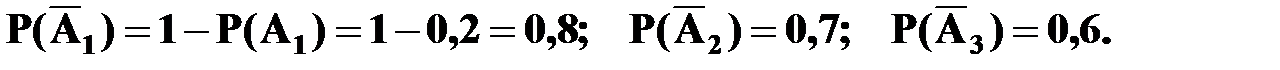
Событие А, состоящее в том, что разрыва цепи не произошло, есть произведение независимых событий 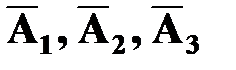 . Следовательно, получаем:
. Следовательно, получаем:
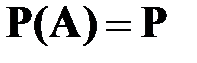
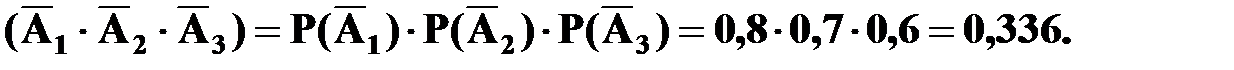
Пример 4. В урне 6 черных, 5 красных и 4 белых шара. Последовательно, один за другим, вынимают три шара. Найти вероятность того, что первый шар окажется черным, второй – красным и третий – белым.
Решение. Рассмотрим следующие события:
А – первый вынутый шар черный,
|
|
|
В – второй шар красный,
С – третий шар белый.
Обозначим через D событие, заключающееся в том, что шары вынуты в последовательности: черный, красный, белый. Событие D= A∙B∙C.
Так как события А, В, С зависимые, то
P (D) = P (A∙B∙C) =P (A) ∙PA(B) ∙PA∙B(C).
Вероятность того, что первоначально вынут черный шар, 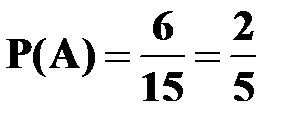 .
.
Вероятность извлечения из урны красного шара при условии, что первоначально был вынут черный шар, РA(В) = 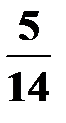 , так как после изъятия черного шара в урне осталось 14 шаров и из них – 5 красных. Вероятность извлечения из урны белого шара после того, как были извлечены черный и красный шары, PA∙B(C)=
, так как после изъятия черного шара в урне осталось 14 шаров и из них – 5 красных. Вероятность извлечения из урны белого шара после того, как были извлечены черный и красный шары, PA∙B(C)= 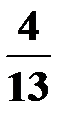 (после изъятия черного и красного шаров в урне осталось 13 шаров и из них – 4 белых).
(после изъятия черного и красного шаров в урне осталось 13 шаров и из них – 4 белых).
Таким образом, P (D) = 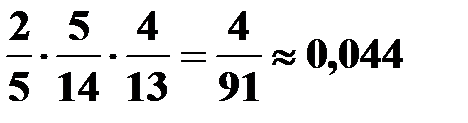 .
.
4
Пример 5. Из колоды, содержащей 36 карт, наудачу вынимают три карты. Найти вероятность того, что среди них окажется хотя бы одна «дама».
Решение. Пусть событие А – среди трех карт окажется хотя бы одна дама. Введем в рассмотрение противоположное событие 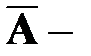 среди вынутых карт нет ни одной «дамы». Найдем Р(
среди вынутых карт нет ни одной «дамы». Найдем Р( 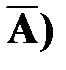 .
.
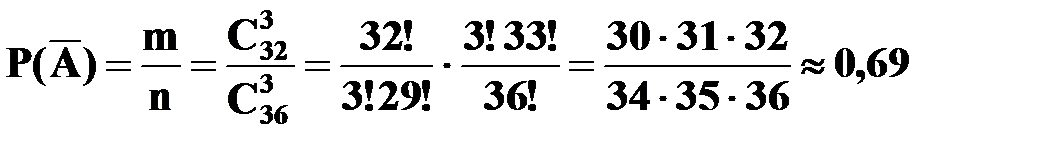 .
.
Тогда P (A) = 1 – P (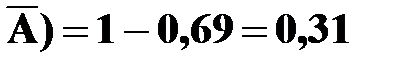 .
.
Пример 6. Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них соответственно равны: 0,7; 0,8; 0,9. Найти вероятность того, что:
а) в цель попадет только третий стрелок;
б) в цель попадет только один стрелок;
в) в цель попадут только два стрелка;
г) в цель попадет хотя бы один стрелок.
Решение. Рассмотрим следующие события:
А1 – первый стрелок попал в цель;
А2 – второй стрелок попал в цель;
А3 – третий стрелок попал в цель.
По условию P(A1)=0,7; P(A2)=0,8; P(A3)=0,9.
|
|
|
а) Пусть событие А – в цель попал только третий стрелок, тогда 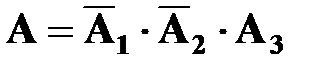 . Так как события
. Так как события 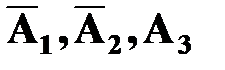 независимые, тогда
независимые, тогда
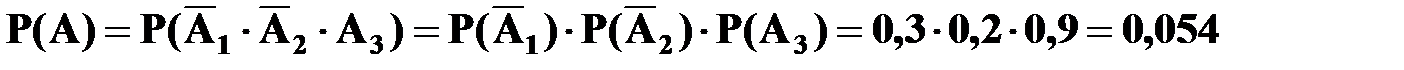 .
.
б) Пусть событие B - в цель попал только один стрелок, тогда
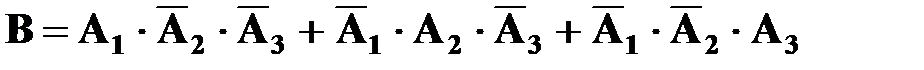
Отсюда, используя теорему сложения для несовместных событий и теорему умножения для независимых событий, имеем:
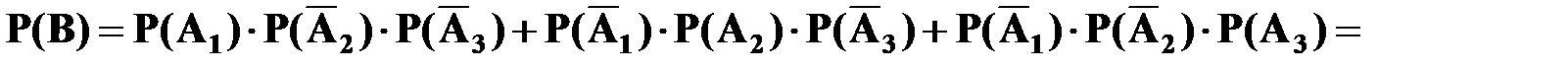
=0,7 ∙ 0,2 ∙ 0,1 + 0,3 ∙ 0,8 ∙ 0,1 + 0,3 ∙ 0,2 ∙ 0,9 = 0,092.
в) Пусть событие С – в цель попадут только два стрелка. Тогда
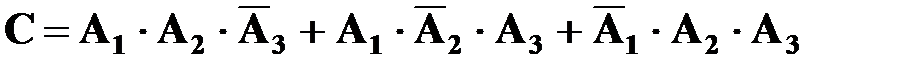 ,
,
откуда
P(C) = 0,7 ∙ 0,8 ∙ 0,1 + 0,7 ∙ 0,2 ∙ 0,9 + 0,3 ∙ 0,8 ∙ 0,9 = 0,398.
г) Пусть событие D - в цель попадет хотя бы один стрелок.
Рассмотрим противоположное событие 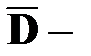 ни один из стрелков в цель не попадет, т.е. все стрелки промахнутся.
ни один из стрелков в цель не попадет, т.е. все стрелки промахнутся.
Так как 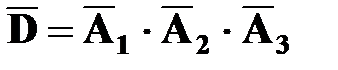 , то
, то
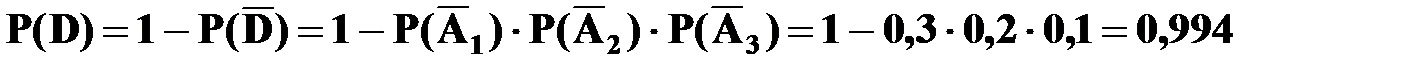 .
.
 2020-10-09
2020-10-09 452
452








