For todo

найти наименьшее а с ;

добавить к множеству E ребро ;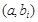

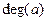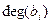уменьшить и на 1.

Добавить к множеству E ребро 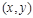, где x и y – позиции ненулевых элементов в таблице степеней.

Код Прюфера устанавливает взаимно однозначное соответствие между множеством всех деревьев с множеством вершин 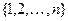и множеством упорядоченных наборов длины , составленных из элементов множества 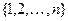. Отсюда следует формула для числа таких деревьев.

Теорема о числе деревьев (формула Кэли). Число помеченных деревьев с вершинами равно .

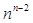Корневым деревом называют дерево с выделенной вершиной – корнем.

Высота корневого дерева – это расстояние от корня до самого удаленного листа.

Если в корневом дереве T путь, соединяющий вершину 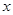с корнем, проходит через вершину 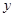, то говорят, что 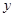– предок 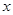, а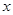– потомок 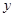. В частности, каждая вершина является предком и потомком самой себя. Множество всех предков вершины 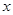порождает путь из корня в 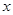. Множество всех потомков вершины 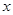порождает дерево с корнем 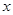, оно называется ветвью дерева T в вершине 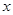. Если предок и потомок соединены ребром, то они называются соответственно отцом и сыном. Компактный и полезный во многих случаях способ задать корневое дерево состоит в указании для каждой вершины ее отца (отцом корня иногда считают саму эту вершину).

Изоморфизм корневых деревьев определяется так же, как изоморфизм графов вообще, но с дополнительным требованием: корень при изоморфизме должен переходить в корень. Проверка изоморфизма корневых деревьев выполняется достаточно легко с помощью специального кодирования. Канонический код 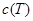дерева 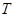можно построить следующим образом.

Каждой вершине 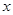дерева 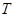приписывается код вершины – слово 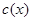в алфавите {0,1}. Он строится по следующим правилам. Если 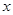– лист (но не корень), то 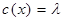, где 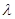– пустое слово. Код вершины 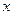, не являющейся листом, определяется после того, как построены коды всех ее сыновей. Пусть 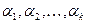– эти коды, упорядоченные лексикографически: 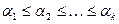. Тогда полагаем 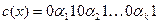. Код корня и является каноническим кодом дерева. На рисунке 4 показаны дерево с корнем в вершине 12 и таблица кодов его вершин.

Теорема об изоморфизме корневых деревьев. Корневые деревья 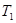и 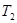изоморфны тогда и только тогда, когда .

Рис. 4.

Канонический код любого дерева обладает свойствами:

1) число нулей в нем равно числу единиц;

2) в каждом его начальном отрезке число единиц не превосходит числа нулей.

Используя эти свойства, можно легко восстановить дерево по его коду. Код дерева 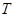имеет вид: 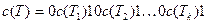, где 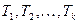– ветви в сыновьях корня. Если 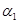– первый начальный отрезок слова 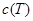, в котором число нулей равно числу единиц, то 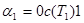. Таким образом, код первой ветви получается из слова 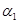отбрасыванием первой и последней букв. Аналогично находятся коды остальных ветвей. Если код какой-то ветви оказывается пустым словом, то эта ветвь состоит из единственной вершины. К остальным ветвям процедура применяется рекурсивно.

Описанное кодирование можно применить и для распознавания изоморфизма обычных (не корневых) деревьев. Допустим, нужно сравнить деревья 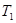и 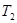. Сначала находим центры обоих деревьев. Ясно, что при изоморфизме центр должен перейти в центр. Если центр каждого из деревьев состоит из одной вершины, выберем эти вершины в качестве корней, затем построим канонические коды корневых деревьев и сравним их. Если центр одного дерева – одна вершина, а другого – две, то эти деревья не изоморфны. Допустим, каждый из центров состоит из двух вершин. Если удалить ребро, соединяющее две центральные вершины, то дерево разобьется на два корневых дерева (с корнями в бывших центральных вершинах). Построив коды этих корневых деревьев, получаем для дерева 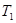пару слов 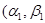), а для дерева 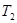– пару слов 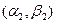. Остается сравнить эти (неупорядоченные) пары.

Пусть G – связный граф. Его каркас (остов, остовное дерево)– это остовный подграф, являющийся деревом. В общем случае (граф может быть несвязным) каркас определяется как лес, в котором каждая компонента связности является каркасом компоненты связности графа. У любого графа есть хотя бы один каркас. Его можно найти, удаляя цикловые ребра (ребра, принадлежащие циклам) до тех пор, пока все циклы не будут разрушены.

Если в графе есть циклы, то у него больше одного каркаса. Определить точное число каркасов связного графа позволяет так называемая матричная теорема Кирхгофа. Для графа G определим матрицу 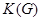– квадратную матрицу порядка n с элементами

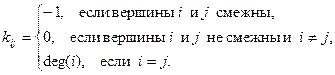
Заметим, что матрица 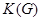– вырожденная, так как сумма элементов каждой строки равна 0.

Теорема Кирхгофа. Если G – связный граф с не менее чем двумя вершинами, то алгебраические дополнения всех элементов матрицы 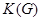равны между собой и равны числу каркасов графа G.