Экстремум функции

Пусть x₀ –внутренняя точка области определения функции y=f(x).

Определение. Говорят, что в точке x₀ функция y=f(x) имеет максимум, если существует такая окрестность этой точки, что для любого x, принадлежащего этой окрестности выполняется условие f(x₀)> f(x); точка x₀ есть точка минимума, если для любого x из этой окрестности f(x₀)< f(x).

x₁, x₃ – точки максимума, x₂, x₄ – точки минимума. (рис. 9.3)

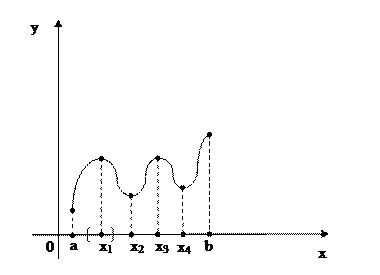
Из определения вытекает локальный характер максимумов и минимумов. Очевидно, возможно существование нескольких максимумов и минимумов. Поэтому не следует путать понятия максимума и наибольшего значения функции, минимума и наименьшего значения функции в рассматриваемой

Рис. 9.3

области. Точкам максимума соответствуют максимальные значения функции, точкам минимума - минимальные значения. Точки минимума и максимума называют точками экстремума, а соответствующие значения функции экстремальными значениями функции f(x). Наибольший из максимумов – глобальный максимум, наименьший из минимумов - глобальный минимум.

Если функция f(x) рассматривается на замкнутом отрезке [a;b], то наибольшего значенияМ она достигает либо в точке глобального максимума, либо на конце отрезка [a;b]; наименьшего значения m – в точке глобального минимума, либо на одном из концов отрезка [a;b]: f(a)=m, f(b)=M.

Подчеркнем, что экстремум может достигаться лишь во внутренних точках рассматриваемой функции (y=sin x, y=x²).

Так как экстремальные значения функции существенно характеризуют поведение функции, то рассмотрим теоремы, которые указывают способы нахождения экстремумов.

Необходимый признак существования экстремума (теорема Ферма).

Теорема 9.2 Если функция y=f(x) непрерывна и дифференцируема в точке x₀ и имеет в ней экстремум, то производная в этой точке f'(x)=0 (Рис. 9.4)

Доказательство. Пусть x₀ –точка максимума. В этом случае f(x₀)> f(x₀+ Δ x), независимо от знака Δ x. Тогда Δy=f(x₀+Δx)-f(x₀)<0, ( Δ x ^>_<0). Если Δ x>0, то 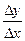<0; если Δ x>0, то 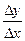>0.

Рис. 9.4

Так как

, ,

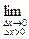
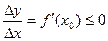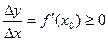то 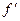(x₀)=0.

Для случая, когда x₀ –точка минимума, доказательство аналогично.

Обратное теореме Ферма утверждение не верно, то есть из условия f'(x)=0, не следует, что x₀ –точка экстремума.

Примеры.

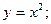
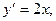
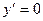при x=0 (Рис. 9.5)

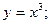
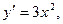
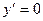при x=0 (Рис. 9.6)

Рис. 9.5 Рис. 9.6

Таким образом, экстремумы функции следует искать среди критических (стационарных) точек. Однако, не всякая стационарная точка является точкой экстремума. Теорема Ферма имеет простое геометрическое истолкование: если x₀ –точка экстремума, то касательная к кривой в этой точке параллельна оси Ox.

Замечание. Если снять требование дифференцируемости в точке экстремума x₀, то возможно в этой точке функция y=f(x) имеет либо бесконечную производную (f'(x)=∞), либо вообще не имеет производной. (Рис. 9.7)

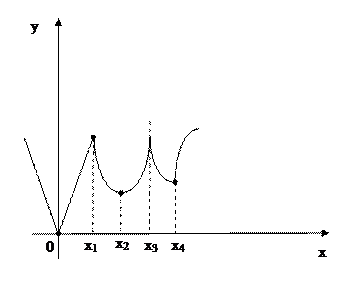
Острые экстремумы в точках x=0, x=x₁, x=x₃ и x=x_4.

x₂ – точка гладкого экстремума.

Рис.9.7

Примеры.

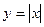(Рис. 9.8 а), 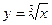(Рис. 9.8 б), 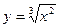(Рис. 9.8 в)

а) б) в)

Рис. 9.8