Решение парных матричных игр с нулевой суммой.
Используя платежную матрицу, определим наилучшие стратегии игроков.
В теории игр предполагается, что противники, участвующие в игре, одинаково разумны, и каждый из них делает все возможное для достижения своей цели.
Проанализируем стратегии игрока I. Первый игрок, выбирая стратегию 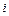 , должен рассчитывать, что второй ответит на нее той из своих стратегий
, должен рассчитывать, что второй ответит на нее той из своих стратегий 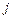 , для которой выигрыш игрока I будет минимальным. Найдем минимальное число
, для которой выигрыш игрока I будет минимальным. Найдем минимальное число 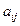 в каждой строке матрицы и, обозначив его
в каждой строке матрицы и, обозначив его  , запишем в добавочный столбец платежной матрицы (см. табл. 2)
, запишем в добавочный столбец платежной матрицы (см. табл. 2)

Зная числа 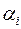 (свои выигрыши при применении всех стратегий и разумных ответах игрока II), первый игрок должен выбрать такую стратегию, для которой
(свои выигрыши при применении всех стратегий и разумных ответах игрока II), первый игрок должен выбрать такую стратегию, для которой 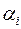 максимально. Обозначив это максимальное значение как
максимально. Обозначив это максимальное значение как 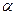 , (т.е.
, (т.е. 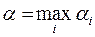 ) и используя (1), получим:
) и используя (1), получим:
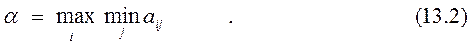
Таблица 13.2
 III III | ... | 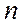 | 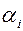 | ||
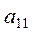 | 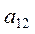 | ... | 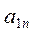 | 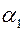 | |
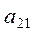 | 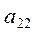 | ... | 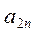 | 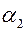 | |
| ... | ... | ... | ... | ... | ... |
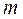 | 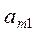 | 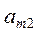 | ... | 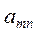 | 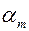 |
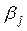 | 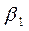 | 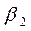 | ... | 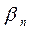 |
Величина 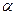 представляет собой гарантированный выигрыш, который может обеспечить себе первый игрок и называется нижней ценой игры (максимином). Стратегия, обеспечивающая получение нижней цены игры
представляет собой гарантированный выигрыш, который может обеспечить себе первый игрок и называется нижней ценой игры (максимином). Стратегия, обеспечивающая получение нижней цены игры 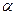 , называется максиминной стратегией. Если первый игрок будет придерживаться этой перестраховочной стратегии, то ему гарантирован выигрыш, не меньший
, называется максиминной стратегией. Если первый игрок будет придерживаться этой перестраховочной стратегии, то ему гарантирован выигрыш, не меньший 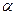 при любом поведении второго игрока.
при любом поведении второго игрока.
В свою очередь, второй игрок стремится уменьшить свой проигрыш или, - что то же самое, - выигрыш первого игрока обратить в минимум. Поэтому для выбора своей наилучшей стратегии он должен найти максимальное значение выигрыша первого игрока в каждом из столбцов и среди этих значений выбрать наименьшее. Обозначим через 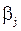 максимальный элемент в каждом столбце
максимальный элемент в каждом столбце 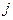 и запишем эти элементы в дополнительной строке табл. 2. Наименьшее значение среди
и запишем эти элементы в дополнительной строке табл. 2. Наименьшее значение среди 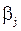 обозначим через
обозначим через 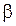 ; эта величина представляет собой верхнюю цену игры (минимакс), которая определяется по формуле:
; эта величина представляет собой верхнюю цену игры (минимакс), которая определяется по формуле:
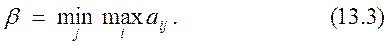

Стратегия игрока II, обеспечивающая «выигрыш» 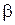 , является его минимаксной стратегией. Выбор минимаксной стратегии игроком II гарантирует ему проигрыш не больше
, является его минимаксной стратегией. Выбор минимаксной стратегии игроком II гарантирует ему проигрыш не больше 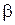 .
.
В теории игр доказывается, что для нижней и верхней цены игры всегда справедливо неравенство:
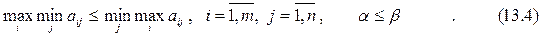
Игры, для которых нижняя цена равна верхней, т. е. 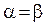 , называются играми с седловой точкой.
, называются играми с седловой точкой.
Общее значение нижней и верхней цены игры в играх с седловой точкой называется чистой ценой игры  , а соответствующие стратегии
, а соответствующие стратегии 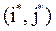 - оптимальными чистыми стратегиями. Эти стратегии определяют положение равновесия, так как каждому из игроков невыгодно отходить от своей оптимальной стратегии. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.
- оптимальными чистыми стратегиями. Эти стратегии определяют положение равновесия, так как каждому из игроков невыгодно отходить от своей оптимальной стратегии. Если игра имеет седловую точку, то говорят, что она решается в чистых стратегиях.
Пример. Компании A и B продают два вида лекарств. Компания A рекламирует продукцию на радио (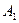 ), телевидении (
), телевидении (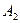 ) и в газетах (
) и в газетах (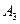 ). Компания B, в дополнение к использованию радио (
). Компания B, в дополнение к использованию радио (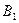 ), телевидения (
), телевидения (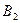 ) и газет (
) и газет (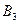 ), рассылает также по почте рекламные проспекты (
), рассылает также по почте рекламные проспекты (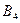 ). В зависимости от качества и интенсивности рекламной компании, каждая из них может привлечь на свою сторону часть клиентов конкурента. В Табл. 3 приведен процент клиентов, привлеченных или потерянных компанией A:
). В зависимости от качества и интенсивности рекламной компании, каждая из них может привлечь на свою сторону часть клиентов конкурента. В Табл. 3 приведен процент клиентов, привлеченных или потерянных компанией A:
Таблица 13.3.
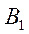 | 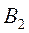 | 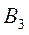 | 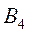 | 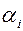 (минимумы строк) (минимумы строк) | |||
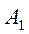 | -2 | -3 | 
| ||||
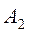 | |||||||
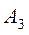 | -2 | -9 | -9 | ||||
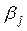 (максимумы столбцов) (максимумы столбцов) |  5 5 |
|
Если компания A выбирает стратегию 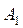 , то, независимо от реакции компании B, наихудшим для нее результатом является потеря 3% рынка в пользу конкурента. Аналогично при выборе стратегии
, то, независимо от реакции компании B, наихудшим для нее результатом является потеря 3% рынка в пользу конкурента. Аналогично при выборе стратегии 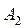 наихудшим исходом для компании A является увеличение рынка на 5% за счет компании B. Наконец, наихудшим исходом при выборе стратегии
наихудшим исходом для компании A является увеличение рынка на 5% за счет компании B. Наконец, наихудшим исходом при выборе стратегии 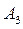 является потеря компанией A 9 % в пользу компании B. Чтобы достичь наилучшего результата из наихудших, компания A должна выбрать стратегию
является потеря компанией A 9 % в пользу компании B. Чтобы достичь наилучшего результата из наихудших, компания A должна выбрать стратегию 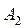 .
.
Рассмотрим теперь стратегии компании B. Так как элементы матрицы являются платежами компании A, то наилучшей для компании B является стратегия  .
.
Оптимальным решением игры является выбор стратегий 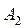 и
и  , т.е. обеим компаниям следует проводить рекламу на телевидении. При этом рынок компании A увеличится на 5 %. Так как в данном случае максимин и минимакс совпадают (5 %), то игра является игрой с седловой точкой, ее цена = 5%, и компании используют стратегии, соответствующие седловой точке.
, т.е. обеим компаниям следует проводить рекламу на телевидении. При этом рынок компании A увеличится на 5 %. Так как в данном случае максимин и минимакс совпадают (5 %), то игра является игрой с седловой точкой, ее цена = 5%, и компании используют стратегии, соответствующие седловой точке.
Решение, соответствующее седловой точке, гарантирует, что ни одной компании нет смысла пытаться выбрать другую стратегию. Действительно, если компания B перейдет к любой другой стратегии (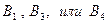 ), то компания A может сохранить свой выбор стратегии
), то компания A может сохранить свой выбор стратегии 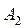 , что приведет к большей потери рынка компанией B (6 или 8 процентов). По тем же причинам компании A нет смысла использовать другую стратегию – если она использует, например, стратегию
, что приведет к большей потери рынка компанией B (6 или 8 процентов). По тем же причинам компании A нет смысла использовать другую стратегию – если она использует, например, стратегию 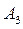 , то компания B может использовать свою стратегию
, то компания B может использовать свою стратегию 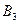 и увеличить свой рынок на 9 %.
и увеличить свой рынок на 9 %.
13.2 Игры без седловых точек. Использование линейной оптимизации
Таким образом, для игр, содержащих седловую точку, нахождение оптимальных стратегий игроков может быть найдено по принципу минимакса. Имеется устойчивая общая стратегия, содержащая пару оптимальных стратегий, и ни одному из игроков невыгодно от них отступать.
Однако большинство игр характеризуется отсутствием в платежной матрице седловых точек. Исход таких игр определить труднее, так как чистой оптимальной стратегии ни для одного из игроков уже не существует. Решение игры в чистых стратегиях отсутствует, и необходимо искать решение в смешанных стратегиях, состоящих в случайном применении двух и более чистых стратегий с определенными вероятностями. Таким образом – смешанная стратегия игрока – это случайная величина, значениями которой являются его чистые стратегии. Для определения смешанной стратегии необходимо указать вероятности (частоты), с которыми выбираются чистые стратегии игрока. При этом предполагается, что игра повторяется многократно и каждый из игроков, с одной стороны, получает информацию о предыдущих ходах противника, а с другой стороны, хочет скрыть от противника свои намерения в будущих ходах.
Смешанные стратегии игроков I и II будем обозначать, соответственно, 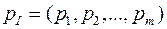 и
и 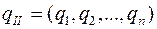 , где
, где 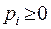 ,
, 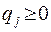 ‑ вероятности применения соответствующих чистых стратегий. Очевидно, должны выполняться условия нормировки для вероятностей:
‑ вероятности применения соответствующих чистых стратегий. Очевидно, должны выполняться условия нормировки для вероятностей:
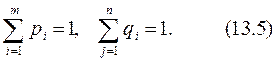
Так как в игре без седловых точек чистые стратегии игроков 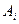 и
и 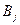 выбираются независимо друг от друга случайным образом с вероятностями соответственно
выбираются независимо друг от друга случайным образом с вероятностями соответственно 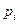 и
и 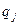 , то вероятность их совместного выбора, и, следовательно, вероятность выигрыша
, то вероятность их совместного выбора, и, следовательно, вероятность выигрыша 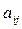 также равна
также равна 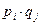 .
.
Средний выигрыш первого игрока равен математическому ожиданию
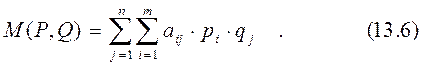
и называется функцией выигрыша первого игрока в смешанных стратегиях. Данную формулу можно записать в матричном виде

где вектор-строка 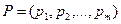 задает вероятности применения различных чистых стратегий первым игроком,
задает вероятности применения различных чистых стратегий первым игроком, 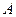 - платежная матрица и
- платежная матрица и 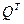 задает вероятности применения чистых стратегий вторым игроком:
задает вероятности применения чистых стратегий вторым игроком:
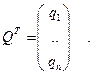
По формуле (13.6) легко найти выигрыши игроков в случае, когда один из них применяет чистую стратегию, а второй – смешанную.
Так, средний выигрыш первого игрока при условии, что он применяет чистую стратегию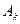 , а игрок B – смешанную стратегию, получается заменой в формулах (13.6) или (13.7) вектор- строки
, а игрок B – смешанную стратегию, получается заменой в формулах (13.6) или (13.7) вектор- строки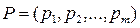 на
на 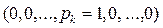 :
:
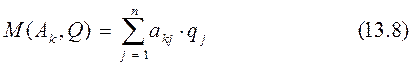
Аналогично, средний выигрыш первого игрока при условии, что он применяет смешанную стратегию, а игрок В – некоторую чистую стратегию 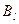 равен:
равен:

Приведем алгоритм нахождения оптимальных смешанных стратегий.
В теории игр доказывается, что каждая игра без седловых точек имеет цену 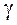 , представляющую средний выигрыш, приходящийся на одну партию и удовлетворяющую условию
, представляющую средний выигрыш, приходящийся на одну партию и удовлетворяющую условию 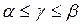 (т. е. лежит между нижней (
(т. е. лежит между нижней (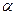 ) и верхней (
) и верхней (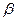 ) ценами игры). Каждый игрок, придерживаясь смешанной стратегии, при многократном повторении игры получает более выгодный для себя результат. Оптимальное решение игры характеризуется тем, что игроки не заинтересованы в отходе от своих оптимальных смешанных стратегий.
) ценами игры). Каждый игрок, придерживаясь смешанной стратегии, при многократном повторении игры получает более выгодный для себя результат. Оптимальное решение игры характеризуется тем, что игроки не заинтересованы в отходе от своих оптимальных смешанных стратегий.
Стратегии, входящие в оптимальные смешанные стратегии, называются активными.
Смешанная стратегия, которая гарантирует игроку наибольший возможный средний выигрыш (или наименьший возможный средний проигрыш), называется его оптимальной смешенной стратегией.
 2014-02-02
2014-02-02 3431
3431








