Доказательство

Доказательство.

Доказательство.

Доказательство.

Доказательство.

Доказательство.

Доказательство.

Доказательство.

.

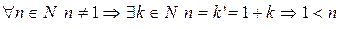2) .

.

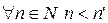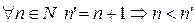3) .

.

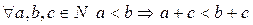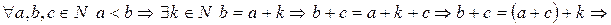
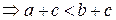4) .

.

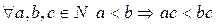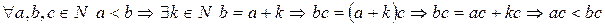5) .

.

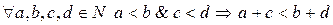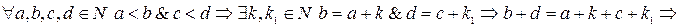
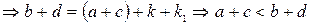6) .

.

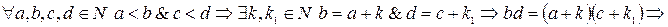
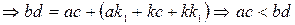7) .

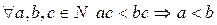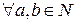возможны случаи:

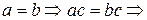§ противоречие с условием ;

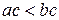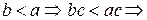§ противоречие с условием ;

§ .

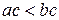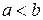Методом исключения получаем, что .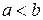

8) .

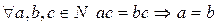Предположим, что 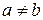. Тогда возможны случаи:

§ ;

§ .

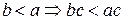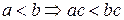В обоих случаях получено противоречие с условием 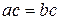, следовательно, предположение неверно.

Определение. Универсальная алгебра 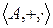называется полукольцом, если бинарные операции + и удовлетворяет следующим условиям: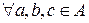

1.;

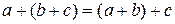2. ;;

3. ;

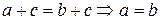4. ;

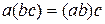5. ;

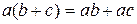6. .

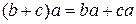Теорема 4. 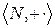- полукольцо.

Доказательство.

Сложение и умножение - операции на множестве натуральных чисел (т еоремы 1,2). Доказательство аксиом полукольца смотри свойства указанных опреаций.

что и требовалось доказать.

Определим на множестве натуральных чисел бинарное отношение 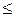по следующему правилу:

.

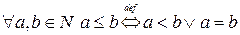Теорема 5. Отношение 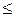на множестве натуральных чисел является линейным порядком (рефлексивно, антисимметрично, транзитивно, линейно).

(доказательство самостоятельно).

Определение. Множество 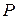называется линейно упорядоченным, если на нем задано бинарное отношение линейного порядка.

Определение. Полукольцо 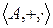называется линейно упорядоченным, если множество 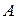линейно упорядочено.

Теорема 6. Полукольцо натуральных чисел линейно упорядочено.

Доказательство.

Следует из теоремы 6.