2014-02-02
933
Теорема 2.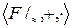 
- поле.
Доказательство.
Поскольку операции сложения и умножения действительных чисел сводятся к операциям сложения и умножения рациональных, то нетрудно проверяется их ассоциативность, коммутативность, дистрибутивность.
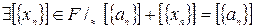(существование 0) (?)
Покажем, что класс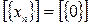 
:
.
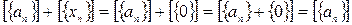(существование 1) (?)
Покажем, что класс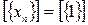 
:
.
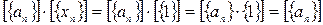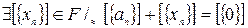(с уществование противоположного) (?)
Проверим, что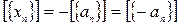 
:
.
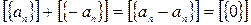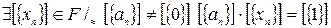
(с уществование обратного для каждого ненулевого) (?)
Поскольку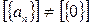 
, 
- ненулевая ф.п.р.ч., следовательно, либо , либо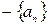 
положительны. Последнее влечет 
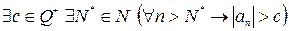. Таким образом, среди членов последовательности , начиная с номера 
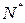нет чисел, равных 0. Рассмотрим 
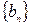- подпоследовательность последовательности такую, что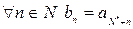 
. Последовательность 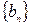не содержит нулевых членов. Зная, что всякая подпоследовательность эквивалентна данной последовательности, имеем 
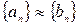. Тогда 
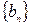. Поскольку ненулевая фундаментальная последовательность рациональных чисел и среди ее членов отсутствуют числа, равные 0, 
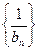является частным фундаментальных последовательностей 
, а, значит тоже фундаментальна.
|
|
|
Проверим, что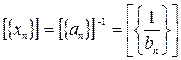 
:
.
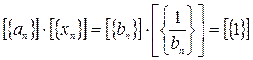что и требовалось доказать.
