Метод скінчених різниць

Тема: Методи розв’язку плоскої задачі теорії пружності.

Решение типовых задач.

Найти интервалы выпуклости и вогнутости, точки перегиба:

а).

1. Область определения функции D(y)=R.

2..

3..

Критические точки второго рода:.,,.

x	(-∞;-1)	x=-1	(-1;1)	x=1	(2,5;+∞)
	+		−		+
	выпукла	точка перегиба y(-1)=-6	вогнута	точка перегиба y(1)=0	выпукла

б).

1. Область определения функции D(y): x¹1.

2..

3.

;

.

Критические точки второго рода:

, т.е. числитель равен нулю Þ не существует;

– не существует, т.е. знаменатель равен нулю Þ.

x	(-∞;1)	x=1	(1;+∞)
	–	не существует	+
	вогнута	не существует	выпукла

Точек перегиба нет.

Точний розв’язок бігармонічного рівняння плоскої задачі в багатьох випадках виявляється дуже складним. Для його спрощення застосовують наближений метод скінчених різниць, який дозволяє замінити диференціальне рівняння системою алгебраїчних рівнянь.

Встановимо залежність між похідними функцій в довільній точці та значенням самої функції в цій та сусідніх точках. На рис. 6.1 зображена крива φ(х) та показані п’ять точок, абсциси яких відрізняються на малу величину ∆ х в точці 0:

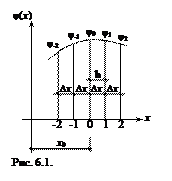
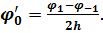(6.1)

Аналогічно можна представити похідну в точці 1:

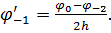
Другу похідну в точці 0 можна отримати, використовуючи двічі першу похідну:

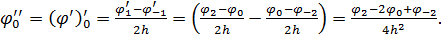
Зменшивши інтервал в двічі, можна отримати більш точну величину другої похідної в точці 0:

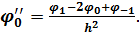(6.2)

Обчислимо третю похідну в точці 0:

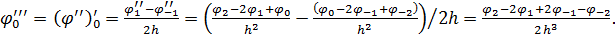
Таким чином: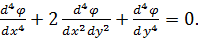

Підставивши в нього вирази четвертих похідних (6.8), (6.9), отримаємо:

.

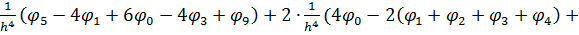
Після спрощення та перетворень бігармонічне рівняння для точки 0, виражене через лінійні алгебраїчні рівняння, набуде вигляду:

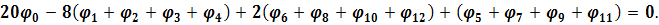
(6.10)

Напруження в точці 0 отримаємо за допомогою формул (5.3), без врахування об’ємних сил:

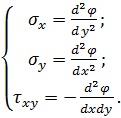
або

(6.11)

Рівняння виду (6.10) можна скласти для кожного з вузлів всередині контура; при цьому в частину рівнянь ввійдуть і значення функції φ для вузлів на контурі та для вузлів, розташованих на відстані одного кроку поза контуром. На рис. 6.2 поза контурна сітка позначена штриховою лінією.

Значення функції φ на контурі та поза контуром знаходять виходячи з граничних умов. Таким чином, невідомих значень функції виявиться стільки, скільки і вузлів в середині контура, при цьому таку ж кількість рівнянь виду (6.10) можна скласти. Відповідно, для розв’язку задачі рівнянь достатньо.

Для визначення значення функції на контурі розглядають значення функції φ на контурі ділянки що досліджується, як згинальний момент в балці с таким же навантаженням, що і на цьому краю ділянки. Дійсно, якщо на верхній грані прямокутної ділянки прикладене навантаження q(x), спрямоване до низу, то для цієї грані можна скласти наступну умову:

(6.12)

Порівнюючи його з залежністю між згинальним моментом та інтенсивністю розподіленого навантаження при згині балок:

можна дійти висновку,що функцію напружень φ на контурі пластини можна прийняти рівною величині згинального моменту в даній точці балки з таким же навантаженням. При цьому балка може мати будь-яке закріплення оскільки його характер впливає тільки на величину сталих, які з’являються після інтегрування співвідношення (6.12):

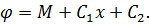(6.13)

На напруження вид закріплення балки впливу не має, оскільки напруження дорівнюють другим похідним функції φ і сталі С₁, С₂ в ці вирази не ввійдуть. На нижній грані пластини функцію φ слід обирати таким чином, щоб вона дорівнювала величині згинального моменту з оберненим знаком.

Похідні функції φ на верхній та нижній гранях , а на бокових представляють собою поперечні сили в відповідних точках балки.

Похідні на верхній та нижній гранях та 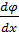на бокових можна знайти використавши формулу:

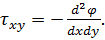
Значення похідних в точках контура можна використовувати і для обчислення, значень функції в точках поза контуром. Так, для точки b (рис. 6.2) відповідно до формули (6.5) можна скласти наступне співвідношення:

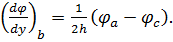
Звідси можна знайти величину функції φ в точці а, розташованій поза контуром пластини:

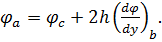(6.14)

Аналогічно для точки ℓ, що лежить на бічній грані,

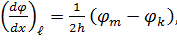
звідки значення функції φ в точці k, що лежить поза контуром пластинки,

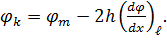(6.15)

Таким чином, плоска задача теорії пружності зведена до визначення величин функції φ(x, y) в усіх вузлах сітки. Для цього маємо стільки рівнянь виду (6.10), скільки вузлів в середині пластини. Значення функції на контурі пластини знаходимо з граничних умов за допомогою співвідношень (6.13), а поза контуром – за допомогою відповідних співвідношень (6.14), (6.15). Розв’язуючи систему рівнянь виду (6.10), знаходимо значення функції φ, а за допомогою рівнянь (6.11) визначають напруження в усіх вузлах сітки.

Метод скінчених різниць особливо ефективний при розрахунку складних пластин, коли контур не прямокутний, коли пластина має отвори і т. ін.