Пара сил. Момент пары сил. Теоремы о парах

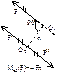
Пара сил – система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной – момент пары.

Он определяется:

Его модулем = F*d. d – расстояние между линиями действия сил пары, называется плечом пары.

Положением в пространстве плоскости действия пары.

Направлением поворота пары в этой плоскости.

Момент пары сил – вектор m(или M), модуль которого равен произведению модуля одной из сил пары, на ее плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

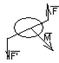
Две пары, лежащие в || плоскостях и имеющие одинаковый момент эквивалентны.

Все пары в пересекающихся плоскостях можно заменить одной парой с моментом, равным сумме моментов этих пар. Для абсолютно твердого тела пара – свободный вектор, определяемы только моментом. Момент перпендикулярен плоскости образуемой парой.

Пару можно заменить параллельной ей равной силе и парой с моментом, равным произведению этой силы на расстояние до новой точки приложения.

Теоремы о парах.

1) Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. .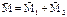

2) Две пары, имеющие геометрически равные моменты, эквиваленты.

3) Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия. Т.е. момент пары сил является свободным вектором.

4) Система нескольких пар сил эквивалента одной паре, момент которой равен векторной сумме моментов данных пар. Т.е. система пар приводится к одной паре, момент которой равен сумме моментов всех пар. Условие равновесия пар сил: 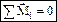– геометрическая сумма их моментов равна 0. Пары сил, расположенные в одной плоскости, взаимно уравновеш-тся, если алгебраическая сумма их моментов åМ_i=0.

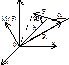
Момент силы относительно точки – вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо "h"– кратчайшее расстояние от точки до линии действия силы. 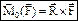– момент силы равен векторному произведению вектора 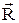на вектор 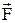. Модуль векторного произведения: 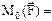R×F×sina = F×h. Для плоской сист. сил обычно находят не вектор момента, а только его модуль: 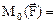± F×h, >0 – против час.стр.; x, F_y, F_z – проекции силы на оси координат и точка 0 – начало координат, то

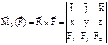= (yF_z – zF_y) + (zF_x – xF_z) 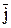+ (xF_y – yF_x) 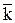, откуда проекции момента силы на оси коорд.: М_0x(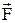) = yF_z – zF_y; М_0y (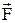) = zF_x – xF_z; М_0z () = xF_y – yF_x.

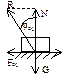
Главный вектор – векторная сумма всех сил, приложенных к телу. Главный момент относительно центра – векторная сумма моментов всех сил, приложенных к телу относительно того же центра.

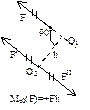
Теорема (лемма) о параллельном переносе силы: сила приложенная в какой-либо точке тверд. тела, эквивалента такой же силе, приложенной в любой др. точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.