Отношения порядка

Слово «порядок» часто применяют в са­мых различных вопросах. Офицер дает команду: «По порядку номе­ров рассчитайся», арифметические действия выполняются в опре­деленном порядке, спортсмены становятся по росту, все ведущие шахматисты располагаются в определенном порядке по так назы­ваемым коэффициентам Эло (американский профессор, который раз­работал систему коэффициентов, позволяющую учитывать все ус­пехи и неудачи игроков), после первенства все футбольные команды располагаются в определенном порядке и т. д. Существует порядок выполнения операций при изготовлении детали, порядок слов в предложении (попробуйте понять, что значит предложение «на он старика посадил осла не»!).

Располагая элементы некоторого множества друг за другом, мы тем самым упорядочиваем их или устанавливаем между ними некоторое отношение по­рядка. Простейшим примером является естественный порядок натуральных чисел. Его естественность заключается в том, что для любых двух натураль­ных чисел мы знаем, какое из них следует за другим или какое из них больше другого, поэтому мы можем расположить натуральные числа в последова­тельности так, что большее число будет расположено, например, правее меньшего: 1, 2, 3,.... Разумеется, последовательность элементов можно вы­писывать в любом направлении, а не только слева направо. Само понятие натуральных чисел уже содержит в себе идею упорядоченности. Устанавливая некоторое относительное расположение элементов какого-либо множества, мы тем самым задаем на нем некоторое бинарное отноше­ние порядка, которое в каждом конкретном случае может иметь свое назва­ние, например, "быть меньше", "быть старше", "содержаться в", "следовать за" и т. д. Символические обозначения порядка также могут быть разнооб­разными, например, 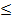, Í, 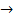и т. д.

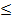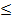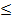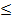Главным отличительным признаком отношения порядка является наличие у него свойства транзитивности. Так, если мы имеем дело с последовательно­стью каких-то объектов x₁, х₂,..., х_n, ..., упорядоченных, например, по отно­шению , то из того, что выполняется х₁ х₂ ... х_п 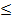..., должно следо­вать, что для любой пары х_i, х_j элементов этой последовательности также выполняется x_i 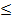x_j:

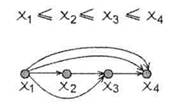
Для пары элементов x_{i 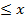j} в графе отношения мы проводим стрелку от вершины x_i к вершине x_j, т. е. от меньшего элемента к большему.

Граф отношения порядка можно упростить, если воспользоваться методом так называемых диаграмм Хассе. Диаграмма Хассе строится сле­дующим образом. Меньшие по порядку элементы располагают ниже, а большие – выше. Поскольку одного такого правила недостаточно для изо­бражения, проводят линии, показывающие, какой из двух элементов больше, а какой меньше другого. При этом достаточно нарисовать лишь линии для непосредственно следующих друг за другом элементов. Примеры диаграмм Хассе показаны на рисунке:

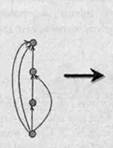
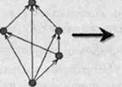
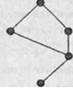
В диаграмме Хассе можно не указывать стрелки. Диа­грамму Хассе можно поворачивать в плоскости, но не произвольно. При поворотах необходимо сохранять относительное положение (выше – ниже) вершин диаграммы:

Отноше­ние R в множестве X называется отношением строгого поряд­ка, если оно транзитивно и асимметрично.

Множество, в котором определено отношение строгого порядка, назы­вают упорядоченным. Например, мно­жество натуральных чисел упорядочено отношением «меньше». Но это же множество упорядочено и другим отношением – «делится на» и «больше».

Граф отношения «меньше» в множестве натуральных чисел можно изобразить в виде луча:

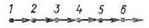
Отношение R в X называется отношением нестро­гого (частичного)порядка, если оно транзитивно и антисимметрично. Всякое отношение нестрогого порядка рефлексивно.

Эпитет "частичный" выражает тот факт, что, возможно, не все элементы множества сравнимы в данном отношении.

Типичными примерами отношения частичного порядка являются отношения "не больше", "не меньше", "не старше". Частица "не" в названиях отношений служит для выражения их рефлексивности. Отношение "не больше" совпада­ет с отношением "меньше либо равно", а отношение "не меньше" то же са­мое, что и "больше либо равно". В связи с этим частичный порядок еще на­зывают нестрогим порядком. Часто отношение частичного (нестрогого) порядка обозначают символом "".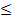

Отношение включения Í между подмножествами некоторого множества также является частичным порядком. Очевидно, что не любые два подмно­жества сравнимы по этому отношению. Ниже на рисунке показан частичный по­рядок по включению на множестве всех подмножеств множества {1,2,3}. Стрелки на графе, которые должны быть направлены вверх, не показаны.

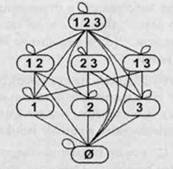
Множества, на которых задан частичный порядок, называют частично упо­рядоченными, или просто упорядоченными множествами.

Элементы х и у частично упорядоченного множества называются сравни­мыми, если х 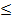у или у 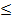х. В противном случае они не сравнимы.

Упорядоченное множество, в котором любые два элемента сравнимы, называется линейно упорядоченным, а порядок – линейным порядком. Линейный порядок еще называют совершенным порядком.

Например, множество всех действительных чисел с естественным порядком 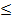, а также все его подмножества, линейно упорядочены.

Объекты самой различной природы могут быть упорядочены иерархически. Вот несколько примеров.

Пример 1. Части книги упорядочены так, что книга содержит главы, главы содержат разделы, а разделы состоят из подразделов.

Пример 2.Папки в файловой системе компьютера вложены друг в друга, образуя ветвящуюся структуру.

Пример 3.Отношение родители – дети может быть изображено в виде так называе­мого генеалогического древа, которое показывает, кто чьим предком (или отпрыском) является.

Иерархический порядок называют древесным (древовидным) потому, что его граф похож на дерево. Древесный порядок является частным случаем строго­го порядка.

Отношение «не длиннее» в множестве отрезков транзитивно и, как легко видеть, рефлексивно. Но оно не является отношением нестрогого порядка, так как нарушено условие антисимметрично­сти: из того, что отрезок х не длиннее отрезка у, а отрезок у – от­резка х, еще не следует совпадение этих отрезков (они могут быть различными, но иметь одну и ту же длину). Рефлексивные и тран­зитивные отношения называют отношениями квазипорядка.

Пусть на множестве А задан частичный порядок 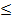. Элемент х называется максимальным (минимальным) элементом множества А, если из того, что х 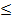у (у 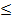х), следует равенство х = у. Иначе говоря, элемент х является максимальным (минимальным), если для любого элемента у или неверно, что х 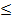у (у 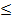х), или выполняется х = у. Таким образом, максимальный (минимальный) элемент больше (меньше) всех отличных от него элементов, с которыми он находится в отношении .

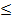Элемент х называется наибольшим (наименьшим), если для любого у Î А выполняется у < х (х< у).

В частично упорядоченном множестве может быть несколько минимальных и/или максимальных элементов, но наименьших и наибольших элементов не может быть больше одного. Наименьший (наибольший) элемент является одновременно и минимальным (максимальным), но обратное утверждение неверно. На рисунке слева показан частичный порядок с двумя минималь­ными и двумя максимальными элементами, а справа – частичный порядок с наименьшим и наибольшим элементами:

В конечном частично упорядоченном множестве всегда суще­ствуют минимальный и максимальный элементы.

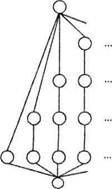
Упорядоченное множество, у которого есть наибольший и наименьший эле­менты, называется ограниченным. На рисунке показан пример бесконечного ограниченного множества. Разумеется, изобразить бесконечное множество на конечной странице нельзя, но можно показать принцип его построения. Здесь петли около вершин не показаны для упрощения рисунка. По той же причине не показаны дуги, обеспечивающие отображение свойства транзитивности. Другими словами, на рисунке представлена диаграмма Хассе отношения порядка.

Бесконечные множества могут не иметь максимальных, или минимальных, или тех и других элементов. Например, множество натуральных чисел (1,2, 3,...) имеет наименьший элемент 1, но не имеет максимальных. Множество всех действительных чисел с естественным порядком не имеет ни наимень­шего, ни наибольшего элемента. Однако его подмножество, состоящее из всех чисел х < 5, имеет наибольший элемент (число 5), но не имеет наи­меньшего.