Отношения эквивалентности

Лекция № 7 Виды бинарных отношений

ЗАКЛЮЧЕНИЕ

Итак, в рамках неклассической философии были сформулированы идеи, “приземлившие” философию И. Канта и Гегеля. Стройные формы её (систематичность, концептуальность, язык, логика, диалектика и т. п.) были отвергнуты или перестали быть обязательными. В философию пришли нерациональные способы познания и выражения мысли. Неклассическая философия как бы вернула человеку человеческое — волю, субъективные переживания, интуицию, мистическую веру, комплексное восприятие жизни. Она предопределила основные направление философии XX ст. в лице экзистенциализма, феноменологии, персонализма, герменевтики, отчасти психоанализа, идею благоговения перед жизнью А. Швейцера и др.

Общее умонастроение неклассической философии подчёркивает несовершенство научно-технического прогресса как идеологии и высвечивает проблему человеческой личности как главную цель философии нашего столетия.

Цель: рассмотреть основные виды бинарных отношений (эквивалентность, отношение порядка, толерантность)

Бинарное отношение может иметь одновременно не­сколько свойств. Некоторые сочета­ния этих свойств определяют особенно интересные отношения, наиболее часто встречающиеся как на практике, так и в математических теориях.

При поломке какой-нибудь де­тали автомобиля ее заменяют другим экземпляром той же детали. Различные экземпляры одной и той же детали неотличимы друг от друга; они, как говорят, эквивалентны (равноценны). Точно так же эквивалентны все монеты одного и того же достоинства и года вы­пуска, все костюмы одной и той же модели и размера, сделанные из одинакового материала, и т. д.

Не всегда эквивалентность сводится к простой одинаковости. Например, если требуется уплатить сумму в 1 руб., то бумажный и металлический рубли эквивалентны друг другу, равно как и 5 двадцатикопеечных монет, или 20 пятачков. В физике считаются эквивалентными взаимозаменяющие друг друга количества энергии (например, 1 ккал эквивалентна 4190 Дж и т.д.).

Выясним, какими общими свойствами обладает отношение вза­имозаменяемости объектов. Во-первых, ясно, что каждый объект может сам себя заменить. Это значит, что для всех х должно выпол­няться отношение xRx, т. е. отношение взаимозаменяемости долж­но быть рефлексивным. Во-вторых, если х взаимозаменяемо с у, то и у взаимозаменяемо с х. Иными словами, если xRy, то и yRx, а потому R симметрично. Наконец, если х взаимозаменяемо с у, а у взаимозаменяемо с z, то х взаимозаменяемо с z. Иными словами, из xRy и yRz следует xRz, т. е. R транзитивно.

Итак, отношение взаимозаменяемости должно обладать свойст­вами рефлексивности, симметричности и транзитивности. Эти свой­ства характеризуют взаимозаменяемость, и потому мы вводим сле­дующее определение:

Отношением эквивалентности в множестве X называется любое рефлексивное, симметричное и транзитивное отношение R.

Приведем примеры таких отношений.

Пример 1. Отношение равенства геометрических фигур рефлексивно (каждая фигура сама себе равна), симметрично (если фигура х равна фигуре у, то и фигура у равна фигуре х) и транзитивно (если фигура х равна фигуре у, а фигура у – фигуре z, то х и z равна). Значит, отношение равенства – эквивалентность в множестве геометрических фигур.

Пример 2. Отношение подобия геометрических фигур также является отношением эквивалентности.

Пример 3. Отношение параллельности прямых также обладает свойствами рефлексивности, симметричности и транзитивности, а потому является отношением эквивалентности в множестве прямых.

Пример 4. Отношение равносильности двух уравнений рефлексивно (каждое уравнение равносильно самому себе), симметрично (если одно уравнение равносильно другому, то и второе равносильно первому) и транзитивно. Значит, оно является эквивалентностью в множестве уравнений.

Пример 5. Отношение равенства дробей тоже является эквивалент­ностью. В самом деле, дроб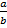и и 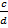равны в том и только в том случае, когда ad = bс. Легко проверяется, что 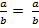(наше равенство принимает вид: аb = аb) и что из 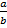= 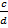следует 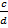= 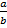(из ad = be следует cb = da). Докажем транзитивность этого отно­шения. Пусть 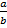= 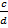и 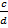= 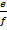. Это значит, что ad = bc и сf = de. Но тогда adf = bcf и bcf = bde, а потому adf = bde. Отсюда получаем, что af = be, а это и значит = .

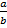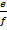Отношение «жить в одном доме» является эквивалентностью в множестве людей (оно рефлексивно, симметрично и транзитивно), а отношение «жить на одной улице» эквивалентностью не является. Дело в том, что человек у может жить в угловом доме на пересече­нии двух улиц, а х и z – на этих улицах. Тогда х и у живут на одной улице, равно как у и z, но х и z живут на разных улицах. Не является эквивалентностью и отношение «служить в одном полку» в множестве военнослужащих. Оно симметрично и транзитивно, но не рефлексивно – есть военнослужащие, не принадлежащие ни­какому полку (например, моряки), и о них нельзя сказать, что они служат в одном полку сами с собой.

Множество всех учащихся данной школы разбито на классы 1А, 1Б,..., 10Б. С этим разбиением свя­зано отношение «учиться в одном классе», являющееся эквива­лентностью.

Непересекающиеся множества, на которые разбивается множество М отношением эквивалентности, называются классами эквивалентности. Другими словами, классом эквивалентности, порожденным элементом х, называется множество всех элементов из М, вступающих с х в отношение эквивалентности. Множество всех различных классов эквивалентности называется фактор-множеством множества М по отношению к эквивалентности R и обозначается М \ R. Например, множество всех рациональных чисел Q можно разбить на классы эквивалентности, для которых 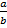– рациональная дробь, где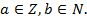

Разбиение множества на попарно непересекающиеся подмноже­ства лежит в основе всех классификаций. Например, в библиотеках множество всех книг разбивают на книги по математике, по физике, по химии, по истории и т. д., в биологии множество всех живых существ разбивают на виды, множество видов – на роды и т. д.