Квазигармоническое представление возможно для любого сигнала, однако, оно наиболее полезно при изучении относительно узкополосных сигналов, у которых ширина спектра Df<<fср. Для таких сигналов огибающая A(t) является низкочастотным процессом, т.е. изменяется медленно по сравнению с изменениями сигнала X(t). Это же верно и для мгновенной начальной фазы 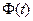 и для ее производной
и для ее производной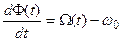 , при условии, что частота 0 выбрана вблизи средней круговой частоты спектра 2pfср. При наблюдении на осциллографе такой процесс имеет вид колебания промоделированного по амплитуде и фазе. Процесс представляет собой синусоиду или косинусоиду с частотой w0 (несущие колебания), амплитуда и фаза которых относительно медленно изменяются в соответствии с законом модуляции A(t) и
, при условии, что частота 0 выбрана вблизи средней круговой частоты спектра 2pfср. При наблюдении на осциллографе такой процесс имеет вид колебания промоделированного по амплитуде и фазе. Процесс представляет собой синусоиду или косинусоиду с частотой w0 (несущие колебания), амплитуда и фаза которых относительно медленно изменяются в соответствии с законом модуляции A(t) и 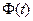 . Функции A(t) и
. Функции A(t) и 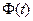 в теории связи обычно представляют собой полезные сообщения, передаваемые с помощью процесса X(t). Выражение для X(t) со (*) можно записать в следующем виде:
в теории связи обычно представляют собой полезные сообщения, передаваемые с помощью процесса X(t). Выражение для X(t) со (*) можно записать в следующем виде:
 ,
,
где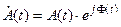 – комплексная огибающая сигнала.
– комплексная огибающая сигнала.
Модуль комплексной огибающей, равный A(t), содержит информацию об амплитудной модуляции колебаний, а фазовый множитель 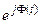 – только об угловой модуляции. В целом же произведение
– только об угловой модуляции. В целом же произведение 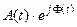 содержит полную информацию о полезном сообщении модулированного сигнала. Это свойство комплексной огибающей обуславливает важность понятия “аналитический сигнал”, поскольку позволяет при анализе узкополосных сигналов исключить из рассмотрения частоту ω0, которая может быть достаточно высокой. Преобразуя последнее выражение для
содержит полную информацию о полезном сообщении модулированного сигнала. Это свойство комплексной огибающей обуславливает важность понятия “аналитический сигнал”, поскольку позволяет при анализе узкополосных сигналов исключить из рассмотрения частоту ω0, которая может быть достаточно высокой. Преобразуя последнее выражение для 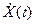 можно записать:
можно записать:
|
|
|
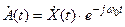
Откуда видно, что комплексную огибающую можно рассматривать как результат сдвига спектра аналитического сигнала на частоту ω0. В отличии от действительной огибающей А(t), комплексная огибающая не определяется однозначно сигналом X(t), а зависит также от выбора в общем случаи произвольной частоты ω0 (за счет изменения ω0 изменяется 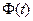 , а следовательно и
, а следовательно и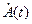 ).
).
Введем обозначения для действительной и мнимой частей комплексной огибающей:
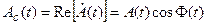
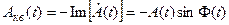
С помощью этих функций можно получить еще одно полезное представление сигналов X(t) и 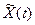 :
:
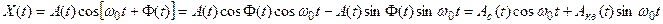
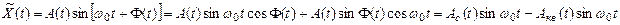
Функции Aс(t) и Aк(t) – называются соответственно синфазной и квадратурной составляющими сигнала X(t). Так же как и 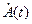 ,они зависят от выбора частоты ω0. Для узкополосного сигнала эти функции, так же как и A(t), являются медленно изменяющимися (низкочастотными).
,они зависят от выбора частоты ω0. Для узкополосного сигнала эти функции, так же как и A(t), являются медленно изменяющимися (низкочастотными).
Рассмотрим два последних выражения как систему уравнений относительно Aс(t) и Aк(t) и решив ее получаем выражение, связывающие эти функции сигналами X(t) и 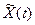 :
:
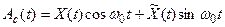
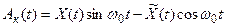
Данные выражения показывают, что функции Aс(t) и Aк(t) являются линейными комбинациями сигналов X(t) и 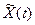 .
.
 2014-02-02
2014-02-02 4668
4668
