Теорема Арцела

Из любой последовательности функций 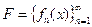, равномерно ограниченных и равностепенно непрерывных на отрезке 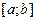, можно выделить подпоследовательность, равномерно сходящуюся на этом отрезке.

Доказательство. Рассмотрим графики функций указанной последовательности. Согласно определению 1, все эти графики на координатной плоскости будут находиться в прямоугольнике 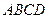со сторонам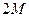и и .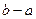

Возьмём последовательность чисел 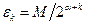, где 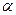- целое положительное число. Каждому 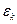поставим в соответствие число 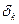из определения 2. Для наглядности выберем 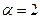. Разобьём прямоугольник 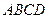на систему одинаковых маленьких прямоугольников горизонтальными и вертикальными линиями, так чтобы расстояние между двумя соседними вертикальными линиями не превосходило 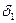, а расстояние между двумя соседними горизонтальными линиями было бы равно 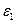. Обозначим вертикальные полосы, составленные из таких прямоугольников римскими цифрами I, II, III и.т.д.

Рисунок.

Для каждой функции последовательности будет выполнено условие

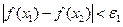при .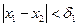

Поэтому график каждой функции последовательности 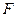может проходить не более чем по двум соседним прямоугольникам полосы I. Однако число таких соседних пар прямоугольников в полосе I конечно (на рисунке оно равно 7), а число функций в последовательности – бесконечно. Тогда в полосе I найдётся хотя бы одна пара соседних прямоугольников, через которую проходит бесконечно много графиков функций рассматриваемой последовательности. Отметим такую пару соседних прямоугольников штриховкой, если же таких пар найдётся несколько, выберем одну из них. Будем далее рассматривать только те функции последовательности, графики которых проходят по выделенному участку полосы I. Перейдём к полосе II. В полосе II функции, проходящие через выделенный участок полосы I, могут занять уже четыре соседних маленьких прямоугольника, но график каждой отдельной функции по-прежнему может проходить не более чем через два соседних прямоугольника полосы II. Таким образом, в полосе II опять найдётся хотя бы одна пара соседних прямоугольников, через которые проходит бесконечное количество графиков функций, проходивших через выделенный участок полосы I. Выделим снова такую пару в полосе II штриховкой и перейдём к полосе III. Теперь рассматриваем только те функции последовательности, графики которых проходят по выделенным участкам полос I и II. Продолжим этот процесс, пока не пройдём весь прямоугольник. В каждой вертикальной полосе будет выделена пара соседних маленьких прямоугольников, через которую проходит бесконечное число графиков функций первоначальной последовательности, и при переходе к следующей вертикальной полосе мы будем рассматривать только эти функции, а остальные отбросим. Выделенные прямоугольники образуют полосу максимальной ширины 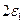. Из всех функций, графики которых проходят по полосе , выберем какую-либо одну и обозначим её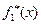. Все остальные функции, графики которых проходят по полосе , назовём семейством . 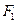Семейство 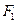так же бесконечно, как и исходное семейство 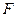. Завершён первый этап доказательства.

Теперь будем рассматривать только функции семейства 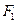. На прямоугольнике 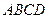сделаем новое разбиение, аналогичное первоначальному, но уже используя величины 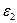и 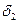. Повторим все построения. Получится новая полоса 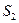, которая лежит внутри первой полосы . Ширина этой новой полосы будет равна 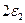. По полосе 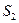будет проходить бесконечное количество графиков функций семейства 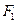. Полученное подсемейство обозначим 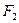, а какую-либо функцию из него обозначим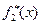. Продолжая этот процесс до бесконечности, получим подпоследовательность 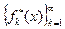первоначальной последовательности 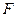. Можно заметить, что начиная с функции 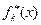, все функции построенной подпоследовательности лежат в полосе 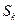шириной 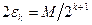. Тогда эта подпоследовательность является фундаментальной, следовательно, для любого 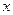из отрезка 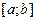последовательность значений этих функций сходится, как фундаментальная последовательность вещественных чисел. Полученную таким образом предельную функцию обозначим 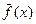. Из приведённых рассуждений следует, что для всех номеров, начиная с номера 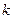, выполняется: 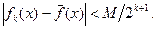Это число одинаково для всех точек отрезка 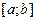, поэтому подпоследовательность 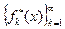равномерно сходится на 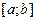. Теорема доказана.