СТОИМОСТЬ, ДОХОДНОСТЬ ЦЕННЫХ БУМАГ
ЛЕКЦИЯ 10
Кредитор, давая деньги в долг, лишается возможности их использовать до момента их возврата. Заемщик должен за это заплатить. Плата за пользование кредитом выражается в форме процента. Процентом называют доход в денежной форме, выплачиваемый кредитору за пользование его деньгами. Процент начисляется на основную сумму займа по определенной процентной ставке с определенной периодичностью. Существуют различные способы начисления процента. Рассмотрим основные из них.
Простые проценты. Пусть имеется некоторая первоначальная сумма средств Р, вкладываемых в некоторое предприятие (банк, инвестиционный проект), в результате чего по истечении определенного периода первоначальная сумма изменяется на величину iР (i - процентная ставка, по которой приращиваются проценты к первоначальной сумме Р). Обозначим через п количество периодов, в течение которых наращивается первоначальная сумма до величины S (наращенная сумма), тогда за п периодов первоначальная сумма Р возрастает на величину iРп и наращенная сумма будет:
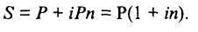
Множитель (1 + in) называется множителем наращения по простым процентам. В рассмотренном случае наращенная сумма S определялась через первоначальную сумму Р; процентную ставку i принято называть декурсивной ставкой.
Можно изменить задачу и попытаться определить первоначальную сумму Р через наращенную S путем ее дисконтирования по процентной ставке d, называемой антисипативной. Тогда
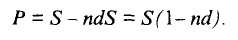
Множитель 1/(1-пd) является множителем наращения.
Простые процентные ставки чаще всего используются в расчетах на короткие периоды (меньше года). В связи с этим следует отметить особенность практики использования декурсивных и антисипативных ставок при п меньше года. В случае декурсивной ставки i принимается 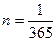 или
или 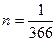 (t - количество дней начисления). Если же используется антисипативная ставка d, то берется
(t - количество дней начисления). Если же используется антисипативная ставка d, то берется 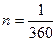
Сложные проценты. Рассмотрим более сложный случай с учетом капитализации процентов. Тогда имеем наращиваемую сумму Р переменной в зависимости от временного периода, так что за i-й период Р увеличивается на ∆Рj:
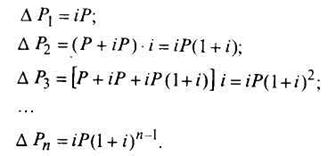
Тогда наращенная сумма

В квадратных скобках имеем сумму геометрической прогрессии, в соответствии с этим получаем:
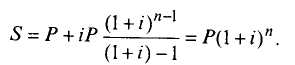
Множителем наращения является величина (1 + i) n. Аналогично можем получить выражение для сложной антисипативной ставки:
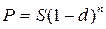
В этом случае множителем наращения выступает 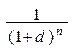
Если п представляет собой нецелое число, например п = k + t (k - количество целых лет, t - количество дней), то для вычисления наращенной суммы S используется выражение
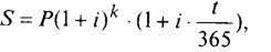
в котором наращение за целые годы определяется по сложным процентам, а за дни - по простым.
Наращенная величина S является суммой, которая будет получена в будущем, а Р –
ее современной величиной. По-другому зависимость 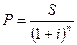 трактуется как приведение величины суммы S, получаемой в будущем, к современному периоду.
трактуется как приведение величины суммы S, получаемой в будущем, к современному периоду.
Если количество лет (n) будет достаточно большим, то современная величина любой суммы, вычисленная как по простым, так и по сложным процентам, будет стремиться к нулю:
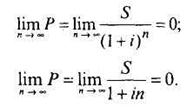
Это означает, что получение любой, даже достаточно большой суммы через много лет в настоящий момент имеет нулевой эффект. Эффект от суммы в будущем уменьшается быстрее, если расчеты ведутся по сложным процентам.
Реальные, номинальные и эффективные ставки процентов. Начисление процентов может производиться с произвольным интервалом. Чаще всего проценты начисляются один раз в год, раз в полгода, раз в квартал, в месяц. Рассмотрим случай, когда проценты начисляются т раз в год (т > 1). За каждый временной период (полгода, квартал, месяц) начисляются j процентов. Процентную ставку, по которой происходит начисление процентов за произвольный период, будем называть реальной процентной ставкой. В нашем случае j - реальная процентная ставка.
При сопоставлении различных инвестиционных проектов возникает потребность сравнить их доходность, но для такого сравнения прежде необходимо доходности (процентные ставки) привести к одному временному периоду. Чаще всего производится приведение процентных ставок к году. При этом могут использоваться различные схемы начисления процентов. Годовая процентная ставка, вычисленная по схеме простых процентов, называется номинальной процентной ставкой. Годовая процентная ставка, вычисленная по схеме сложных процентов, называется эффективной процентной ставкой.
Обозначим iн и iэ - номинальную и эффективную процентные ставки соответственно. За т временных периодов получим наращенную сумму (по схеме простых процентов)
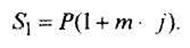
По номинальной процентной ставке наращенная сумма:
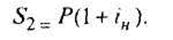
Из равенства S1 и S2 получим i н = тj. По схеме сложных процентов за т временных периодов наращенная сумма
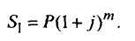
По эффективной процентной ставке наращенная сумма за год
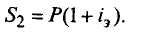
Из равенства S1 = S2 получим:
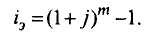
Учитывая, что i н = mj, можно найти связь между номинальной и эффективной процентными ставками:
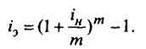
Денежный поток, внутренняя норма доходности. Денежные выплаты, порождаемые какой-либо ценной бумагой, происходят в разное время. Например, купонная облигация в течение всего срока существования порождает ряд разновременных купонных выплат и выплату номинала при погашении. По акции выплачиваются дивиденды в течение всего срока ее нахождения у инвестора.
Денежные выплаты, поступающие в разное время в течение некоторого периода, называются денежным потоком. При приведении будущих денежных поступлений к текущему моменту времени их нужно дисконтировать с учетом длины временного периода, через который будет произведен платеж. Предположения, что в конце первого временного периода поступит сумма, равная S1, в конце второго периода - S2, в конце n -го периода - Sп, тогда текущая стоимость такого денежного потока будет
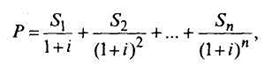
где i - доходность альтернативного вложения (банковская депозитная ставка).
Можно рассмотреть задачу иначе. Предположим, что текущая стоимость денежного потока Р, порождаемого какой-либо ценной бумагой, равна ее рыночной стоимости С, тогда можно определить величину процентной ставки r, при которой Р = С из уравнения
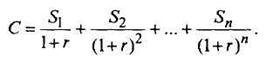
Процентная ставка r, вычисленная при условии равенства текущей стоимости денежного потока его рыночной стоимости, называется внутренней нормой доходности.
Важным и широко используемым при определении стоимости и доходности ценных бумаг является понятие ренты. Под рентой понимается ряд последовательных платежей через равные промежутки времени. В практике финансовых расчетов используется множество различных видов рент. Здесь будут рассмотрены только ренты, использующиеся при оценке стоимости и доходности ценных бумаг:
• постоянная ограниченная рента;
• постоянная вечная рента;
• переменная рента с постоянным приростом платежей.
Постоянная ограниченная рента. Предположим, что в какое-либо мероприятие помещена некоторая сумма, дающая ежегодный доход R в течение п лет (п < 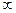 ). Первая выплата производится через год, величина ее равна R, с приведением к настоящему моменту - R/(1 +i). Современная величина следующей выплаты - R/(1+ i)2 и т.д. За п лет современная величина ренты
). Первая выплата производится через год, величина ее равна R, с приведением к настоящему моменту - R/(1 +i). Современная величина следующей выплаты - R/(1+ i)2 и т.д. За п лет современная величина ренты
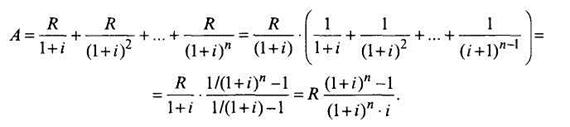
Величина 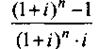 называется коэффициентом приведения ренты.
называется коэффициентом приведения ренты.
Определим наращенную сумму ренты:
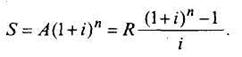
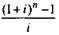 Величина называется множителем наращения ренты.
Величина называется множителем наращения ренты.
Если начисление процентов производится т раз в год по годовой номинальной ставке i, то количество периодов начисления равно т • п и
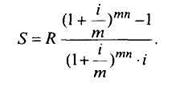
Постоянная вечная рента. Этот вид ренты отличается от предыдущего тем, что постоянные выплаты R производятся вечно, т.е. п = 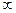 . Чтобы определить современную величину такой ренты, нужно взять предел:
. Чтобы определить современную величину такой ренты, нужно взять предел:
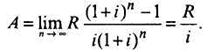
Если же начисление процентов производится т раз в году, то
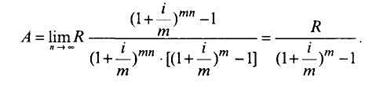
Переменная рента с постоянным приростом платежей. Для этого типа ренты имеем изменяющуюся величину рентных платежей за п лет:
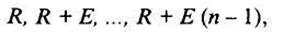
где Е - постоянный ежегодный прирост платежей.
Современная величина такой ренты
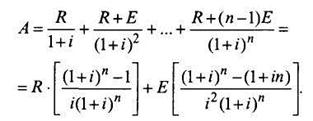
Если рассмотреть этот тип ренты в вечном варианте, то
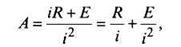
т.е. вечная переменная рента отличается от вечной постоянной на слагаемое E/i2.
Наращенная величина переменной ренты
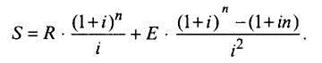
 2014-02-02
2014-02-02 912
912







