М
r1
r2
F1 O F2 х
F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0)
с – половина расстояния между фокусами;
a – большая полуось;
b – малая полуось.
Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
a2 = b2 + c2.
Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r1 + r2 = 2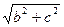 (по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r1 + r2 = a – c + a + c. Т.к. по определению сумма r1 + r2 – постоянная величина, то, приравнивая, получаем:
(по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r1 + r2 = a – c + a + c. Т.к. по определению сумма r1 + r2 – постоянная величина, то, приравнивая, получаем:

a2 = b2 + c2
r1 + r2 = 2a.
Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

е = с/a.
Т.к. с < a, то е < 1.
Определение. Величина k = b/a называется коэффициентом сжатия эллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса.
Коэффициент сжатия и эксцентриситет связаны соотношением:

k2 = 1 – e2.
Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.
Если для точки М(х1, у1) выполняется условие: 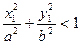 , то она находится внутри эллипса, а если
, то она находится внутри эллипса, а если 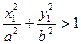 , то точка находится вне эллипса.
, то точка находится вне эллипса.
 Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:
Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения:
r1 = a – ex, r2 = a + ex.
Доказательство. Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать:
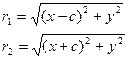
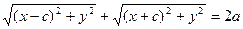
После возведения в квадрат и приведения подобных слагаемых:
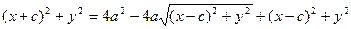
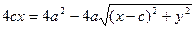
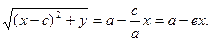
Аналогично доказывается, что r2 = a + ex. Теорема доказана.
С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a/e; x = -a/e.
Теорема. Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.
Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением: 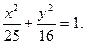
1) Координаты нижней вершины: x = 0; y2 = 16; y = -4.
2) Координаты левого фокуса: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0).
3) Уравнение прямой, проходящей через две точки:
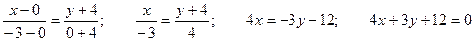
Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.
Уравнение эллипса имеет вид: 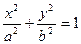 . Расстояние между фокусами:
. Расстояние между фокусами:
2c = 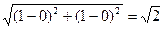 , таким образом, a2 – b2 = c2 = ½
, таким образом, a2 – b2 = c2 = ½
по условию 2а = 2, следовательно а = 1, b = 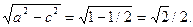
Итого: 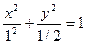 .
.
Гипербола.
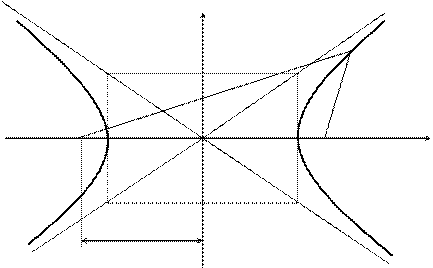
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
 y
y
M(x, y)
b
r1
r2
x
а
F1 F2
c
По определению ïr1 – r2ï= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.
Выберем на гиперболе произвольную точку М(х, у). Тогда:
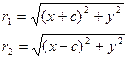
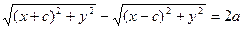
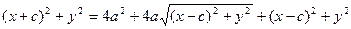
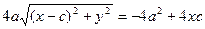

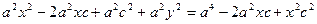
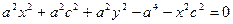
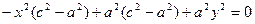
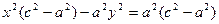
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
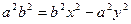

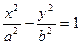
Получили каноническое уравнение гиперболы.
Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью гиперболы.
 Ось 2b называется мнимой осью гиперболы.
Ось 2b называется мнимой осью гиперболы.
Гипербола имеет две асимптоты, уравнения которых 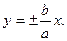
Определение. Отношение 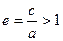 называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а2 = b2:
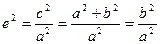
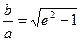
Если а = b, e = 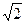 , то гипербола называется равнобочной (равносторонней).
, то гипербола называется равнобочной (равносторонней).
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: 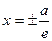 .
.

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.
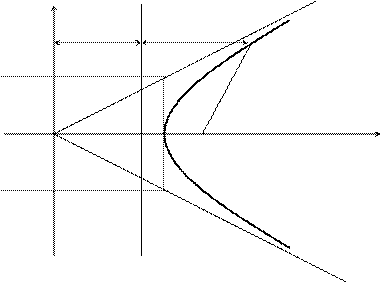
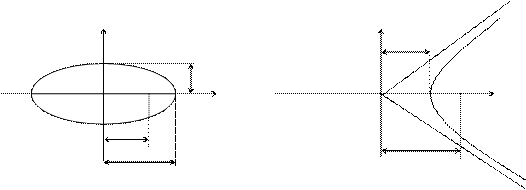
Доказательство. Изобразим схематично гиперболу.
 y
y
a/e d
M(x, y)
r1
0 a F1 x
OF1 = c
Из очевидных геометрических соотношений можно записать:
a/e + d = x, следовательно d = x – a/e.
(x – c)2 + y2 = r2
Из канонического уравнения: 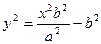 , с учетом b2 = c2 – a2:
, с учетом b2 = c2 – a2:
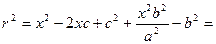
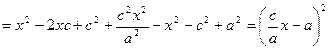
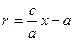
Тогда т.к. с/a = e, то r = ex – a.
Итого: 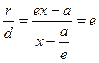 .
.
Для левой ветви гиперболы доказательство аналогично. Теорема доказана.
Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 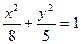 .
.
Для эллипса: c2 = a2 – b2.
Для гиперболы: c2 = a2 + b2.
 |
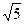
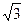
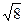
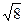
Пример. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением 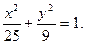
Находим фокусное расстояние c2 = 25 – 9 = 16.
Для гиперболы: c2 = a2 + b2 = 16, e = c/a = 2; c = 2a; c2 = 4a2; a2 = 4;
b2 = 16 – 4 = 12.
Итого: 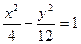 - искомое уравнение гиперболы.
- искомое уравнение гиперболы.
Парабола.
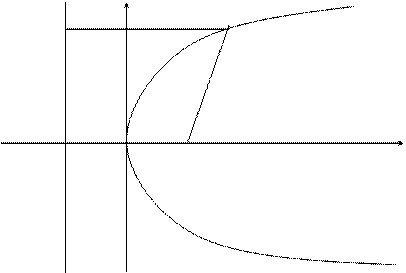
Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расположим начало координат посередине между фокусом и директрисой.
 у
у
 А М(х, у)
А М(х, у)
 |
О F x
 |
p/2 p/2
Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы.
Из геометрических соотношений: AM = MF; AM = x + p/2;
MF2 = y2 + (x – p/2)2
(x + p/2)2 = y2 + (x – p/2)2
x2 +xp + p2/4 = y2 + x2 – xp + p2/4

y2 = 2px
Уравнение директрисы: x = -p/2.
Пример. На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4.
Из уравнения параболы получаем, что р = 4.
r = x + p/2 = 4; следовательно:
x = 2; y2 = 16; y = ±4. Искомые точки: M1(2; 4), M2(2; -4).
 2014-02-03
2014-02-03 2405
2405

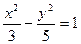 .
.






