Движение точки под действием центральной силы. Закон

11.9. Движение точки под действием центральной силы. Закон

 

Как уже отмечалось, движение материальной точки под действием центральной силы происходит с постоянным вектором момента количества движения . Причем, так как вектор , согласно равенству (11.14), перпендикулярен сомножителям векторного произведения  и , траекторией точки служит плоская кривая.

Сравнивая выражение (11.14) для вектора  и выражение (1.22) для секторной скорости точки , равенство (11.13) можно переписать в виде

 

;

 

 и утверждать, что движение материальной точки под действием центральной силы происходит с постоянной секторной скоростью, то есть радиус-вектор

точки в равные промежутки времени описывает равные площади. Это утверждение получило название закона площадей. Если учесть равенство (1.22), выражающее секторную скорость точки при задании ее движения в полярных координатах, то закон площадей можно представить таким образом

                                                       .                                       (11.25)

 

11.10. Формулы Бинэ.

Французский математик, механик и астроном Жак Филипп Бинэ (1786 – 1856 г.г.) предложил формулы, позволяющие определять скорость материальной точки, которая движется под действием центральной силы, и действующую силу, если известны траектория движения точки и ее секторная скорость.

    Рассмотрим движение точки в полярных координатах. Для квадрата скорости точки можем записать

 

                                             ;                                         (11.26)

 

где радиальная и трансверсальная составляющие скорости точки.

В выражениях (1.14) для  и  от аргумента  перейдем к аргументу 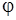. Находим

                                      .                                  (11.27)

 

Введем новую переменную

 

для которой

.

Отсюда

 

Подставив это выражение в равенство (11.27), получим

 

.

Учитывая, что через переменную 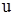 трансверсальная составляющая скорости

точки представляется в виде

 

после подстановки новых выражений для  и  в равенство (11.26), будем иметь

                                       .                                   (11.28)

 

Это – первая формула Бинэ или формула Бинэ для скорости. С помощью формулы (11.28) определяется скорость материальной точки по известной

секторной скорости в любой точке заданной траектории.

    Для вывода второй формулы Бинэ используем дифференциальную форму теоремы об изменении кинетической энергии

 

                                            .

Перепишем это равенство в виде

 

                                                ;

 

и разделим левую и правую части этого равенства на

 

 

Вводя переменную 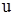 и подставив выражение (11.28)

 

получим

                                                                           (11.29)

 

Вторая формула Бинэ или формула Бинэ для силы (11.29) по известной секторной скорости определяет силу, действующую на материальную точку в любой точке заданной траектории.