Признаки существования предела
Теорема 1. Если числовая последовательность { аn } монотонна и ограничена, то она имеет предел.
Теорема 2. Если в некоторой окрестности точки х0 (или при достаточно больших значениях х) функция f (x) заключена между двумя функциями φ(x) и ψ(x), имеющими одинаковый предел А при x → x0, (или x → ∞ ), то функция f (x) имеет тот же предел А.
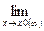 φ(x) = А,
φ(x) = А, 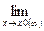 ψ(x) = А.
ψ(x) = А.
Рассмотрим числовую последовательность аn = 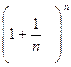 . Если вычислять значения членов последовательности, то получим а1 = 2,0, a2 = 2, 25, a3 = 2, 37, a4 = 2, 441, a5 = 2, 448, …… и можно предположить, что последовательность { аn } является возрастающей. Действительно, воспользуемся формулой бинома Ньютона:
. Если вычислять значения членов последовательности, то получим а1 = 2,0, a2 = 2, 25, a3 = 2, 37, a4 = 2, 441, a5 = 2, 448, …… и можно предположить, что последовательность { аn } является возрастающей. Действительно, воспользуемся формулой бинома Ньютона:
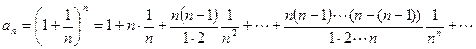
или
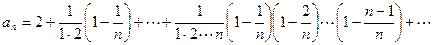
С ростом n увеличивается как число положительных слагаемых (их в формуле n + 1), так и величина каждого слагаемого, т.е. а1 < а2 <…..< аn <…..
Последовательность { аn }является ограниченной.
Определение. Число е (вторым замечательным пределом) называется предел числовой последовательности
е = 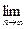
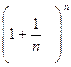 .
.
Выше мы фактически установили, что 2 < е < 3. Более точно e ≈ 2,718281…, т.е. число е - иррациональное число.
|
|
|
Можно показать, что функция 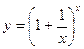 при х → +∞ и при х → -∞ (где х в отличие от натурального числа n "пробегает" все значения числовой оси - не только целые) имеет предел, равный числе е:
при х → +∞ и при х → -∞ (где х в отличие от натурального числа n "пробегает" все значения числовой оси - не только целые) имеет предел, равный числе е:
е = 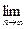
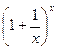 .
.
Полагая 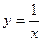 , найдем
, найдем 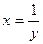 ; при х → ∞ у → 0.
; при х → ∞ у → 0.
В результате получается еще одна запись числа е:
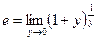 .
.
 2014-02-09
2014-02-09 1267
1267








