Это уравнение приводится к уравнению (n-k)-го порядка

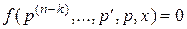
с помощью замены .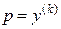

2) Уравнение вида:

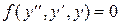, (3)

не содержащее явным образом x.

Для решения введем также функцию:

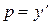(4)

Только теперь аргументом функции р будет y, то есть:

p=p(y). (5)

Тогда по правилу дифференцирования сложной функции получим:

,

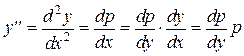То есть

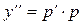. (6)

Подставив (4),(6) в (3), получим уравнение

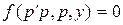, (7)

являющееся уравнением первого порядка относительно функции (5).

Теперь для того, чтобы из решения p = p (y) уравнения (7) получить решение у=y(x) уравнения (3) нужно решить ещё одно уравнение 1^го порядка: ,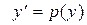

которое является уравнением с разделяющимися переменными.

Замечание. Аналогично, с помощью подстановки (4)-(6) понижается порядок уравнения вида:

.

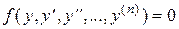Пример 1. Решить уравнение:

.

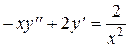Это уравнение не содержит y. Полагая 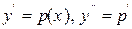, получим линейное уравнение 1^го порядка:

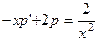. (8)

Решение его ищем по известному методу в виде: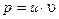.После подстановки в (8) получим:

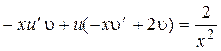. (9)

Функцию 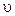подберем из уравнения: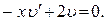

После “разделения переменных” из соотношения 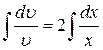найдем ненулевое частное решение: 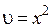. Тогда уравнение (9) примет вид

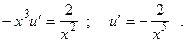
Отсюда

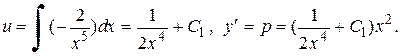
Проинтегрировав, получим общее решение исходного уравнения:

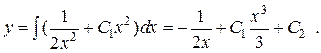
Пример 2. Решить задачу Коши.

В это уравнение не входит x. Порядок уравнения понизим с помощью подстановки: y’=p, где p=p(y). Тогда согласно (6), 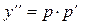и исходное уравнение примет вид:

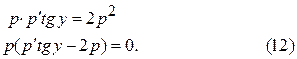
1. Случай: p =0. Отсюда 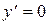, то есть y=C=const.

2. Случай: p ¹0, тогда p^’tg y=2p.

Это уравнение с разделяющимися переменными относительно функции p=p(y).

Разделим переменные: 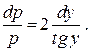Проинтегрируем это равенство:

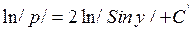, где 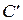=const.

Выразим р: 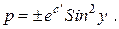Отсюда, учитывая 1 случай, запишем общее решение уравнения (12) 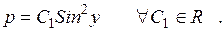Теперь для решения исходного уравнения имеем уравнение с разделяющимися переменными:

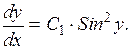(13)

Решаем его по плану:

1. Из уравнения 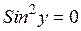найдем частные постоянные решения:

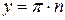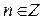, (14)

2. В области, где 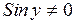, разделим переменные:

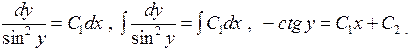
Это равенство есть общий интеграл исходного уравнения, а равенства (14) задают особые решения.

Особые решения (14) не удовлетворяют начальным условиям (10), (11).

Подставив начальное условие (10) в общий интеграл, получим: .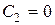

При x =0 из равенств (10),(11) и (13) найдем C₁ = -1. Поэтому Ctg y=x.

Ответ: у=arcctg(x).

Тема 5: Линейные уравнения второго порядка с постоянными коэффициентами.