Решение нелинейных уравнений

Глава 2. Численные методы

Итоги главы

End.

Begin

Begin

Begin

P:=1;

for i:=2 to f do

P:=P*i;

Fkt:=P;

end;

procedure Swap(var s1, s2: real);

var tmp:real;

tmp:=s1;

s1:=s2;

s2:=tmp;

end;

writeln('vv ddwsdvcsdf');

readln(n,m,k);

a:=Fkt(n);

b:=Fkt(m+2)*3;

c:=Fkt(Fkt(k)+1);

if (b>c) and (b>a) then swap(a,b);

if (c>b) and (c>a) then swap(a,c);

if (c>b) then swap(b,c);

writeln('a=', a,'b=', b,'c=',c);

Итак, мы рассмотрели синтаксические и семантические основы языка программирования Turbo Pascal, а также привели несколько типовых вычислительных алгоритмов. Следующий шаг на пути освоения программирования – применение полученных знаний для решения прикладных задач, разработки прикладных программ.

В следующей главе мы рассмотрим, как язык программирования и типовые алгоритмы применяются для реализации численных методов решения математических задач.

Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством вычислений и использованием компьютеров. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач.

К задачам вычислительной математики относят:

§ решение систем линейных уравнений;

§ нахождение собственных значений и векторов матрицы;

§ нахождение сингулярных значений и векторов матрицы;

§ решение нелинейных алгебраических уравнений;

§ решение систем нелинейных алгебраических уравнений;

§ решение дифференциальных уравнений (как обыкновенных дифференциальных уравнений, так и уравнений с частными производными);

§ решение систем дифференциальных уравнений;

§ решение интегральных уравнений;

§ задачи аппроксимации;

§ задачи интерполяции;

§ задачи экстраполяции.

Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел. Поэтому важную роль в вычислительной математике играют оценки точности получаемых результатов. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространенный в линейной алгебре метод, основанный на вычислении определителя матрицы и ее дополнения, требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений.

Если алгебраическое или трансцендентное уравнение достаточно сложно, то его сравнительно редко удается решить аналитическими методами. Более того, в некоторых случаях коэффициенты уравнения известны лишь приближенно, и сама задача о точном определении корней теряет смысл. Поэтому важное значение приобретают способы приближенного нахождения корней уравнения и оценки их точности. Пусть дано уравнение:

,

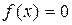где функция f(x) определена и непрерывна в некотором конечном или бесконечном интервале 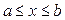. Всякое значение ξ, обращающее функцию f(x) в нуль, т.е. такое, что f(ξ) = 0, называется корнем уравнения. Будем предполагать, что уравнение имеет лишь изолированные корни, т.е. для каждого из них существует окрестность D, не содержащая другие корни (рис. 26). Решить уравнение численными методами – это значит определить, имеет ли оно корни, сколько их и найти корни с заранее заданной точностью. Для решения уравнений вида разработано много различных итерационных методов. Сущность этих методов заключается в следующем.

Рисунок 26 – Решение уравнения

Пусть известна достаточно малая область D, в которой содержится единственный корень ξ уравнения. В этой области выбирается точка x0 – начальное приближение – и строится последовательность точек x1,x2,…xn,…, сходящаяся к ξ, с помощью некоторого рекуррентного соотношения:

.

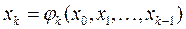Рекуррентное вычисление повторяется до тех пор, пока абсолютное значение разницы между двумя последовательными значениями х не станет меньше некоторого значения е, называемого точностью:

^.

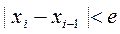Выбирая различными способами функции φk, которые зависят от функции f и номера k, можно получить различные методы.

Численное решение нелинейных уравнений
методом итерации

Заменим уравнение

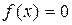
равносильным ему уравнением

^.

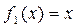И исходное и полученное уравнения имеют одинаковый корень x (рис. 27) и называются эквивалентными.

Вы­бе­­­рем любым спо­со­бом х₀, которое затем под­­­­ста­­вим в левую часть урав­­­не­ния:

^.

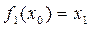По­лу­чен­ное значение х₁ снова под­­ста­вим в ле­вую часть и получим:

^.

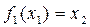Про­дол­жая этот про­цесс, получим по­сле­до­ва­тель­ность чи­­сел х₁, х₂,..., x_n, ко­торая мо­жет либо схо­дить­ся, т.е. иметь предел, ли­бо рас­хо­дить­ся, т.е. не иметь предела. Тогда в со­­ответствии с по­лу­чен­ным результатом в первом слу­чае этот предел является кор­­нем урав­­нения (х ® x), во втором случае сде­лаем вы­­вод о не­воз­можности по­лу­чения ре­ше­ния дан­ным спо­со­бом.

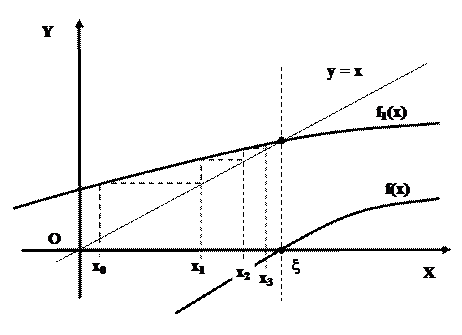
Рисунок 27 – Геометрическая интерпретация итерационного метода решения уравнения

Алгоритм реализации данного метода будет схож с алгоритмом рекуррентного вычисления бесконечной суммы.

Приведём программу, реализующую итерационный метод уточнения корня уравнения:

^.

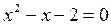program Iter;