Лекция № 13-15 Приложение производной в экономике

Список используемой литературы

Приложение производной в экономике.

Рассмотрим понятие, иллюстрирующее экономический смысл производной. Издержки производства у будем рассматривать как функцию выпускаемой продукции х. Пусть ∆х- прирост продукции, тогда ∆у- приращение издержек производства и 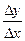- среднее приращение издержек производства на единицу продукции.

Производная 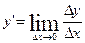выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.

Предельные издержки зависят от уровня производства (количества выпускаемой продукции) х и определяются не постоянными производственными затратами, а лишь переменными (на сырье, топливо, т.п.).

Аналогичным образом могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и другие предельные величины.

Предельные величины характеризуют не состояние, а процесс, изменения экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Однако экономика не всегда позволяет использовать предельные величины в силу неделимости многих объектов экономических расчетов и прерывности экономических показателей во времени (годовых, квартальных, месячных и т.д.). Вместе с тем в ряде случаев можно отвлечься от дискретности и эффективно использовать предельные величины.

Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции.

Определение: Эластичностью функции Е_х(у) называется предел отношения относительного приращения функции у к относительному приращению переменной х при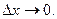

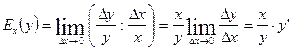
Эластичность функции показывает приближенно, на сколько процентов изменится функция у=f(x) при изменении независимой переменной х на 1%.

Отметим свойства эластичности функции.

1. Эластичность функции равна произведению независимой переменной х на темп изменения функции 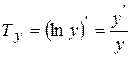т.е. .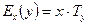

2. Эластичность произведения (частного) двух функций равна сумме (разности) эластичности этих функций.

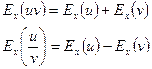
Эластичность функции применяется при анализе спроса и потребления. Если 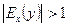, то спрос считают эластичным, если 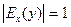- нейтральным, 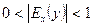- неэластичным относительно цены (или дохода).

Тесты для самоконтроля знаний

1. Если f’(x)>0 на (а; в), то f (x) на [ а; в ]

а) возрастает б) убывает в) не изменяется.

2. Если f’(x) при переходе через х₀ меняет знак с (+) на (-), то в х₀ функция достигает:

а) min б) mах в) f (x0)=с.

3. Если f’’(x) при переходе через х₀ меняет знак, то х₀ является точкой:

а) перегиба б) max в) min.

4. х=а называется вертикальной асимптотой, если:

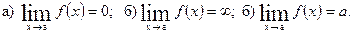
5. Если f’’(x)>0, то график функции:

а) выпуклый б) вогнутый в) разрывна.

1. Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.1. – М.: ОНИКС. 2003. – 304 с.
2. Данко, П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов. Ч.2. – М.: ОНИКС. 2003 – 415 с
3. Ермаков, В.И. Сборник задач по высшей математике. Учебное пособие. –М.: ИНФРА-М, 2006. – 575 с
4. Ермаков, В.И. Общий курс высшей математики. Учебник. –М.: ИНФРА-М, 2003. – 656 с.
5. Колесников, А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М.,2001, - 208 с.
6. Кремер, Н.Ш. Высшая математика для экономистов: Учебник для вузов. - М.: ЮНИТИ, 2004. – 471 с.

Тема «Интегральное исчисление»

Цель: раскрытьпонятия первообразной и неопределенного интеграла, рассмотреть таблицу основных интегралов и методы интегрирования.

Ключевые слова: первообразная, неопределенный интеграл.

Вопросы:

1.Понятия первообразной и неопределенного интеграла.

2.Свойства неопределенного интеграла.

3.Геометрический смысл неопределенного интеграла.

4.Таблица основных интегралов.

5.Методы интегрирования. Интегрирование разложением.

6.Непосредственное интегрирование.

7. Интегрирование методом замены переменной (или интегрирование подстановкой).

8.Интегрирование по частям.

9.Интегрирование некоторых тригонометрических функций.

10.Интегрирование простейших рациональных дробей.

1. Понятие первообразной и неопределенного интеграла

Основная задача дифференциального исчисления состоит в нахождении по данной функции ее производной или дифференциала, т.е. дана функция F(x), найти F`(x)=f(x) и dF(x)=F`(x)dx=f(x)dx (1).

Многочисленные вопросы науки и техники приводят к постановке обратной задачи: для данной функции f(x) найти такую функцию F(x), производная которой равнялась бы заданной функции f(x), т.е. F`(x)=f(x) или dF(x)=f(x)dx (2).

Определение. Первообразной функцией от данной функции f(x) называется функция, производная которой равна данной функции или дифференциал которой равен выражению f(x)dx.

Теорема. Любая непрерывная на сегменте функция имеет на этом сегменте первообразную.

Если функция F(x) – первообразная от функции f(x) а сегменте a ≤ x ≤ b, то всякая другая первообразная от f(x) отличается от F(x) на постоянное слагаемое, т.е. может быть представлена в виде F(x)+С, где С – постоянная.

Определение. Если F(x) – одна из первообразных для функции f(x), то выражение F(x)+C, где С – произвольная постоянная, называется неопределенным интегралом.

Неопределенный интеграл обозначается символом

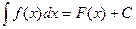(3)

f(х) называется подынтегральной функцией, f(x)dx – подынтегральным выражением.

Действие отыскания неопределенного интеграла – нахождение всех первообразных от данной функции называется интегрированием этой функции.

Операция интегрирования функции является обратной для операции дифференцирования функции.