Работа со сводными таблицами.
Редактирование диаграммы
Размещение диаграммы
Выбор типа диаграммы
Построение диаграмм и графиков в Excel.
Диаграмма представляет собой вставной объект, внедренный на один из листов рабочей книги. Диаграмма сохраняет связь с данными, на основе которых была построена, и при их изменении немедленно меняет свой вид.
Для создания большинства диаграмм, например для линейчатых диаграмм и гистограмм, можно воспользоваться данными из строк и столбцов листа (Лист. Основной документ, используемый в Microsoft Excel для хранения данных и работы с ними. Он также называется электронной таблицей. Лист состоит из ячеек, упорядоченных в строки и столбцы. Листы всегда хранятся в книге.). Однако для некоторых типов диаграмм, например для круговых и пузырьковых, требуются специально организованные данные.
На первом этапе работы выбирается форма диаграммы.
Втрой этап служит для выбора данных.
Третий этап состоит в выборе оформления диаграммы. На вкладках задаются:
· заголовок диаграммы, подписи осей (вкладка Заголовки)
· отображение и маркировка осей координат (вкладка Оси)
отображение сетки дополнительных линий (вкладка Линии сетки)
· описание построенных графиков (вкладка Легенда)
· отображение надписей, соответствующих отдельным элементам данных на графике (вкладка Подписи данных)
· представление данных, использованных при построении графика, в виде таблицы (вкладка Таблицы данных)
Диаграмма может распологаться на этом же или отдельном листе.
Готовая диаграмма состоит из набора отдельных элементов (ряды данных, оси, подписи, область построения и пр.), формат каждого из которых можно изменить. Для зтого нужно раскрыть контекстное мень выделенного объекта, или открыть окно форматирования через меню Формат.
Сводные таблицы
Сводная таблица служит для быстрого подведения итогов или объединения больших объемов данных. создание сводных таблиц осуществляется с помощью Мастера сводных таблиц. Этапы работы мастера:
1. На первом этапе выбираем, откуда выбираются данные: из одного диапазона, разных диапазонов или внешних источников.
2. Собственно выбор диапазонов
3. Макетирование сводной таблицы: необходимо мышью перетащить кнопки полей.
50. Работа с надстройками «Пакет анализа» и «Поиск решения». Подбор параметра.
Excel имеет большие возможности для работы с различными математическими средствами, позволяющими решать самые разнообразные инженерно-технические и научные задачи. Большинство из них не входят в базовый набор функций Excel, аподключаются дополнительно. Наиболее часто используемое средство Поиск решения, а также мощный инструмент обработки статистических данных Пакет анализа.
Для подключения Пакет анализа и других вспомогательных средств следует сделато следующее:
1. Вызвать меню кнопки Office  (расположена в верхнем левом углу окна Excel). Внизу находится вкладка Параметры Excel.
(расположена в верхнем левом углу окна Excel). Внизу находится вкладка Параметры Excel.
1. Щелкнуть вкладку Параметры Excel.
2. Выбрать команду Надстройки и в окне Управление выберите пункт Надстройки Excel.
3. Нажать кнопку Перейти.
4. В окне Доступные надстройки установить флажок Пакет анализа, а затем нажать кнопку ОК.
Совет. Если Пакет анализа отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.
В случае появления сообщения о том, что пакет статистического анализа не установлен на компьютере и предложения установить его, нажмите кнопку Да.
5. После загрузки пакета анализа в группе Анализ на вкладке Данные становится доступной команда Анализ данных.
Основные надстройки, поставляемые вместе с пакетом Excel:
- Пакет анализа. Обеспечивает дополнительные возможности анализа наборов данных.
- Мастер суммирования. Позволяет автоматизировать создание формул для суммирования данных в столбце таблицы и использовать частичные суммы.
- Мастер подстановок. Автоматизирует создание формулы для поиска данных в таблице по названию столбца и строки и использовать поиск с параметром.
- Поиск решения. Используется для решения задач оптимизации.
Средство Поиск решения.
Запускается командой Вкладка Поиск решения. Элементы диалогового окна:
| установить целевую ячейку | - адрес ячейки с целевой функцией |
| Равной | - значение, к которому стремиться целевая функция |
| изменяя ячейки | - адреса влияющих ячеек |
| Параметры | - открывает окно для задания ограничений на значения влияющих ячеек |
средства Поиск решения
Возьмем систему уравнений:
x^2+y^2=3 (1)
2x+3y=1
Решения этой системы удовлетворяют и следущему уравнению:
(х^2+y^2 – 3)^2+(2x+3y-1)^2=0 (2)
Вместо (1) решается (2).
В основу метода положено то, что геометрически решения системы (1) описывают точки пересечения прямой с окружностью радиуса равному корень из 3. Для применения метода Поиск решения теперь важно найти начальное приближение. В данном случае можно протабулировать левую часть уравнения (2) по переменным х и у на интервале (–1.7, +1.7) с шагом 0.3. Границы такие взяты на основании того, что корни уравнения лежат внутри круга радиус которого приблизительно равен 1.73 (корень из 3).
Вычисляется таблица табуляции по 12 значениям х и столько же у.
Выполняются следующие шаги:
1. В ячейки А2:А13 вводятся значения х (в интервале [–1.7, 1.7]), а в ячейки В2:M1 значения y в таком же интервале.
2. В ячейку В2 вводится формула =($A2^2+B$1^2-3)^2+(2*$A2+3*B$1-1)^2 (соответствующая формуле (2)).
3. Заполняется копированием прямоугольный диапозон значений в ячейках B2:M13.
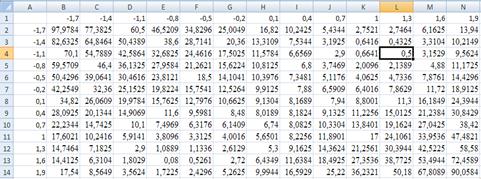
4. В соответствии с формулой (2) за начальные значения х0 и y0 берутся значения х и y в тех ячейках заполненного в п.3 диапазона, где они принимают наименьшие значения.
5. Под значения первого корня отводятся ячейки А16:В16, а А17:В17 – под значения второго корня.
6. Для системы (1), в соответствии с полученной таблицей (для значение 0,4325), мы вводим в А16 значение 1.3, в В16 значение –1.4. В ячейку С16 вводим формулу =(А16^2+В16^2-3)^2+(2*A16+3*B16-1)^2.
7. Теперь применяется функция Данные – Поиск решения.
В диалоговом окне устанавливаем Целевая ячейка $C16, Изменяя ячейки – $A16:$B16, установить параметр Минимальному значению – Выполнить.
Значение корней уравнения появятся в ячейках А16 и В16. Второй корень находим аналогично.
 2014-02-24
2014-02-24 2952
2952
