Дифференциальные уравнения с разделяющимися переменными
Данные уравнения являются наиболее простыми из дифференциальных уравнений. Однако решение многих типов дифференциальных уравнений сводится к решению дифференциальных уравнений с разделяющимися переменными.
В общем случае данные уравнения можно записать в виде
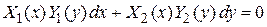
или
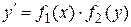 ,
,
где  - непрерывные функции.
- непрерывные функции.
Для нахождения общего решения уравнения переменные x и y в уравнении с помощью алгебраических действий разделяют так, чтобы в каждом слагаемом уравнения содержалась только одна переменная и ее дифференциал, либо x и dx, либо y и dy. Дифференциалы dx и dy. должны быть всегда в числителях дробей.
Разделяем переменные. Уравнение вида 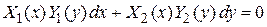
делим на 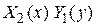 , получаем
, получаем 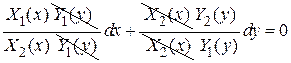 Þ
Þ
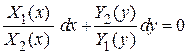 .
.
После того, как переменные разделены, решение уравнения сводится к интегрированию. Записываем
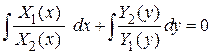 .
.
Таким образом, решение дифференциального уравнения сводится к нахождению интегралов.
Если уравнение имеет вид 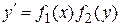 , то переменные разделяем следующим образом
, то переменные разделяем следующим образом
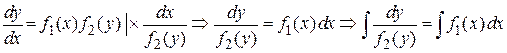 .
.
Если решение дифференциального уравнения сведено к нахождению интегралов, то считается, что оно в принципе решено. Поэтому часто говорят не решить, а проинтегрировать дифференциальное уравнение.
Пример 7.7. Для дифференциального уравнения  найти общее решение и частное решение, удовлетворяющее начальным условиям:
найти общее решение и частное решение, удовлетворяющее начальным условиям: 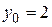 при
при 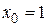 . Построить несколько интегральных кривых.
. Построить несколько интегральных кривых.
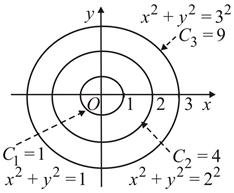 Рис. 82
Рис. 82
|
Находим 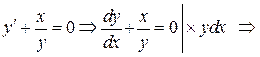
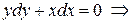 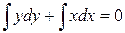 Þ Þ 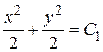 Þ Þ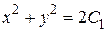 .
Общий интеграл уравнения можно записать в виде .
Общий интеграл уравнения можно записать в виде 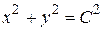 , где , где 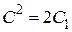 .
Интегральными кривыми являются окружности радиуса С (рис. 82) .
Интегральными кривыми являются окружности радиуса С (рис. 82)
|
Найдем частное решение. Подставим значения 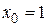 и
и 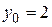 в общий интеграл, получим
в общий интеграл, получим 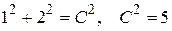 . Частный интеграл
. Частный интеграл 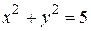 .
.
Пример 7.8. Найти частное решение дифференциального уравнения 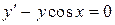 , если при х = 0
, если при х = 0 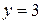 .
.
Разделим переменные и проинтегрируем
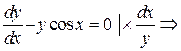
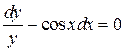 Þ
Þ
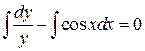 Þ
Þ 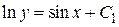 Þ
Þ
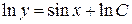 , где
, где 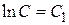 .
.
Тогда 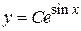 .
.
Произвольная постоянная в решениях дифференциальных уравнений может принимать любые значения 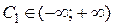 . Данный интервал также является множеством значений логарифма
. Данный интервал также является множеством значений логарифма 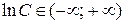 . Поэтому при записи общего решения для более удобного вида часто произвольную постоянную представляют в виде логарифма, а затем освобождаются от логарифмов (потенцируют).
. Поэтому при записи общего решения для более удобного вида часто произвольную постоянную представляют в виде логарифма, а затем освобождаются от логарифмов (потенцируют).
Отметим также следующее. В тех случаях, когда при интегрировании дифференциальных уравнений появляются логарифмы, обычно модули под логарифмами не ставят в расчете на то, что при нахождении частных решений выражения под логарифмами будут положительными за счет выбора начальных условий.
Найдем значение произвольной постоянной при 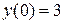 . Получаем
. Получаем 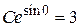 , отсюда С = 3. Частное решение
, отсюда С = 3. Частное решение 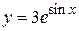 .
.
Пример 7.9. Решить дифференциальное уравнение 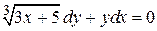 при начальных условиях х = 1
при начальных условиях х = 1 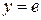 .
.
Разделим переменные и проинтегрируем
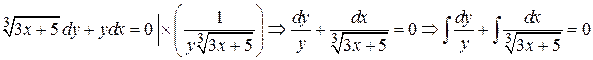 .
.
Находим 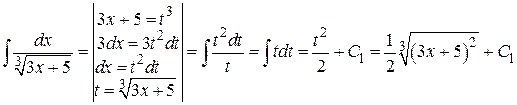 .
.
Получаем 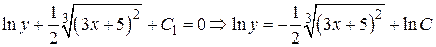 ,
, 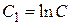 .
.
Общее решение 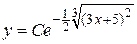 .
.
Подставим начальные условия 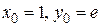 в общее решение, найдем значение произвольной постоянной
в общее решение, найдем значение произвольной постоянной 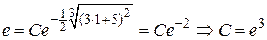 .
.
Частное решение 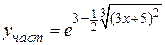 .
.
(дифференциальные уравнения с однородными функциями)
Функция 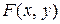 называется однородной n -го измерения, если
называется однородной n -го измерения, если 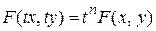 , где t – параметр.
, где t – параметр.
Например, для функции  находим
находим
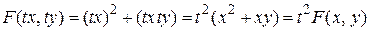 .
.
Следовательно, эта функция второго измерения (n = 2).
Покажем, что частное двух однородных функций 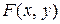 и
и 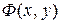 одного и тоже измерения есть однородная функция нулевого измерения. Действительно,
одного и тоже измерения есть однородная функция нулевого измерения. Действительно,
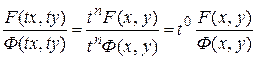 .
.
Однородными дифференциальными уравнениями называются уравнения вида
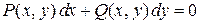 ,
,
где  и
и 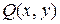 - однородные функции одного измерения.
- однородные функции одного измерения.
Данное уравнение можно привести к уравнению с разделяющимися переменными. Для этого преобразуем уравнение
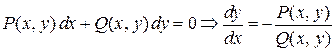 .
.
Обозначим 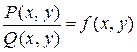 . Тогда уравнение примет имеет вид
. Тогда уравнение примет имеет вид
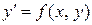 ,
,
где 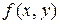 - однородная функция нулевого измерения, т. е.
- однородная функция нулевого измерения, т. е.
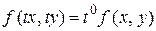 .
.
Если принять параметр 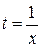 , то
, то 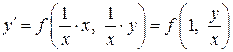 .
.
Уравнение 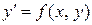 сводится к уравнению с разделяющимися переменными с помощью подстановки
сводится к уравнению с разделяющимися переменными с помощью подстановки
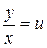 или
или  ,
,
где u = u (x)- функция от x.
Найдем производную 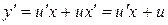 и подставим ее в уравнение, получим
и подставим ее в уравнение, получим
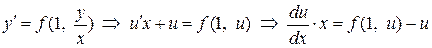 .
.
Разделим переменные и проинтегрируем
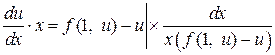 Þ
Þ 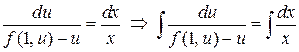 .
.
Решение уравнения сведено к нахождению интегралов. В результате интегрирования будет получен общий интеграл 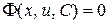 . Для нахождения общего интеграла исходного дифференциального уравнения необходимо сделать обратную замену переменной
. Для нахождения общего интеграла исходного дифференциального уравнения необходимо сделать обратную замену переменной 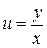 , в результате которой общий интеграл будет иметь вид
, в результате которой общий интеграл будет иметь вид
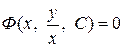 .
.
Пример 7.10. Решить уравнение 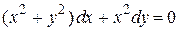 ; при х = 1 y = 1.
; при х = 1 y = 1.
Используем подстановку  . Находим
. Находим 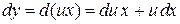 и подставляем в уравнение. Получаем
и подставляем в уравнение. Получаем
 .
.
Сгруппируем отдельно слагаемые с 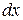 и
и 
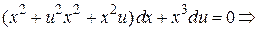
 .
.
Разделим переменные и проинтегрируем
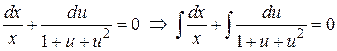
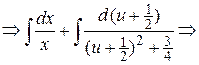
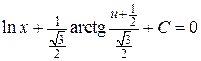 .
.
Выполним обратную подстановку 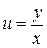 , запишем общий интеграл
, запишем общий интеграл
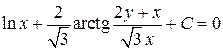 .
.
Найдем значение произвольной постоянной С, соответствующее начальным условиям 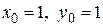 .
.
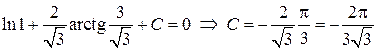 .
.
Запишем частное решение
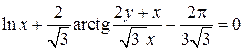 .
.
Пример 7.11. Решить уравнение 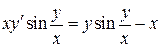 ; при х = 1
; при х = 1 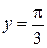 .
.
Используем подстановку  . Найдем
. Найдем 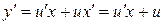 . Подставим y и
. Подставим y и 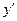 в уравнение, получим
в уравнение, получим
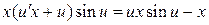 .
.
В этом уравнении сгруппируем в одном слагаемом 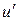 , а в другом все остальные слагаемые, получим
, а в другом все остальные слагаемые, получим
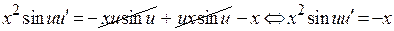 .
.
Учитываем, что 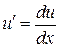 , имеем
, имеем
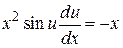 .
.
Разделим переменные и проинтегрируем
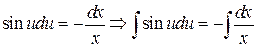 .
.
Получаем
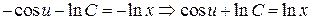 Þ
Þ 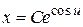 .
.
Выполняем обратную замену переменной 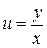 , получаем общий интеграл
, получаем общий интеграл
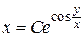 .
.
Находим значение произвольной постоянной.
При 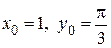 получим
получим 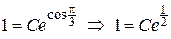 Þ
Þ 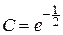 .
.
Записываем частное решение
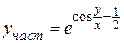 .
.
 2014-02-02
2014-02-02 1240
1240








