Критерий Михайлова. Тривиальное решение уравнения устойчивости системы

Тривиальное решение уравнения устойчивости системы:

a_o·y⁽ⁿ⁾ + a₁·y^(n-1) + … + a_n-1·y' + a_n·y = 0, необходимо и достаточно, чтобы:

1) ¦ (i·w) при 0 ≤ w < +¥ совершил поворот j = n ·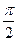, т.е. сделал 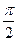оборотов против часовой стрелки;

2) годограф ¦ (i·w) 0 ≤ w < +¥ не проходил через 0;

Для решения этого выражения необходимо и достаточно, чтобы годограф проходил n квадрантов против часовой стрелки, окружая начало координат.

Координаты уравнений u(w) = 0 и v(w) = 0 должны поочередно обращаться в 0.

Другая формулировка:

…..,необходимо и достаточно, чтобы все корни уравнений u(w) = 0 и v(w) = 0 были вещественными и перемежающимися.

u(0)> 0, v(0)> 0

u(w) = a_n – a_n-2·w² + a_n-n·wⁿ – …

v(w) = a_n-1·w – a_n-3·w³ – a_n-5·w⁵ – …

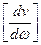_w=0 > 0

Примеры:

u(w) = a_n – a_n-2·w² + a_n-n·wⁿ – …

v(w) = a_n-1·w – a_n-3·w³ – a_n-5·w⁵ – …

w = 0: u(w) = a_n

v(w) =0

1) a_о = 1,тогда i·w + a₁ = 0

2) уравнение 2-й степени:

р²+ а₁·р + а₂ = 0; ¦ (p) = ¦ (i·w) = –w² + i· a₁·w + a₂ = u(w) + i·v(w)

u(w) = –w²+ a₂

v(w) = a₁·w

3) уравнение 3-й степени:

р³+ а₁·р² + а₂·р + а₃ = 0; ¦ (p) = ¦ (i·w) = –i·w³ + a₁·w² + a₂·w + a₃ = u(w) + i·v(w)

u(w) = a₃ – a₁·w²

v(w) = a₂·w – w³

4) уравнение 8-й степени

Неустойчивые решения:

D – разбиения

Введение:

Однородное линейное дифференциальное уравнение n – го порядка:

a_o·y⁽ⁿ⁾ + a₁·y^(n-1) + … + a_n-1·y' + a_n·y = 0 (*)

Алгебраическое уравнение:

a_o·рⁿ + a₁·p^(n-1) + … + a_n-1·p + a_n = 0 (**)

2 постановки задачи:

1) коэффициенты уравнения (*) считаются заданными, и ищется ответ – устойчива система или неустойчива.

2) при фиксированном значении коэффициентов находим, при каких условиях решение устойчиво.