Обратные операторы

Лекция 2 Обратные операторы. Теорема Банаха об обратном операторе и ее следствия

2.1. Обратные операторы

2.2. Теорема Банаха об обратном операторе и ее следствия

Многие задачи, встречающиеся в теории дифференциальных уравнений, интегральных уравнений и других приложениях, могут быть записаны в виде уравнений

A x = y, (1)

где x – неизвестная функция из некоторого пространства X; y – известная функция из некоторого пространства Y; A – заданный линейный оператор из пространства X в пространство Y. При исследовании уравнения (1) необходимо по возможности дать ответы на следующие вопросы: 1) существует ли решение уравнения (1) для произвольного y; 2) единственно ли это решение; 3) если не единственно, то сколько решений существует; 4) если не для любого y существует решение, то какие условия нужно наложить на y для существования решения; 5) как найти x точно или приближенно.

Рассмотрим, с какими свойствами оператора A связаны перечисленные свойства уравнения (1).

Определение 2.1. Пусть A : X ® Y. Оператор B : Y ® X называется правым обратным к оператору A, если A B = I_Y. Оператор B называется левым обратным к оператору A, если B A = I_X. Оператор B называется обратным к оператору A (обозначается A ^–¹), если A B = I_Y, B A = I_X, т. е. является одновременно левым обратным и правым обратным.

Заметим, что в определении не выдвигается требование линейности или ограниченности оператора B.

Множество Ker A ={ x : x Î A, A x =0} называется ядром оператора A, множество Im A ={ y : $ x Î X, y = A x } – образом оператора A.

Лемма 2.1. Для линейного оператора A следующие утверждения эквивалентны:

1) решение уравнения A x = y единственно для любого y ÎIm A;

2) Ker A ={0};

3) для оператора A существует левый обратный оператор.

Доказательство. 2))1). Если A x ₁= y и A x ₂= y, т. е. x ₁ и x ₂ – два решения, то A (x ₁– x ₂)=0 и x ₁= x ₂.

1))2). Достаточно положить y =0.

1))3). Для y ÎIm A существует и единственно решение уравнения A x = y. Построим оператор B, который y ÎIm A ставит в соответствие решение x (для остальных y оператор B определен произвольным образом или вообще не определен). Тогда если y = A x, то по построению B y = B A x = x, т. е. B A = I_X.

3))1). Если существует левый обратный оператор B к оператору A и если A x ₁= y, A x ₂= y, то x ₁= B y, x ₂= B y, т. е. x ₁= x ₂. Лемма доказана.

Лемма 2.2. Следующие утверждения эквивалентны:

1) решение уравнения A x = y существует для любого y Î Y;

2) Im A = Y;

3) для оператора A существует правый обратный оператор B.

Доказательство. Эквивалентность 1),2) следует из определения множества Im A.

1))3). Для каждого y Î Y выберем одно из решений x ^* уравнения A x = y. Тем самым определено отображение B : Y ® X, B y = x ^*. По построению если B y = x ^*, то x ^* – решение уравнения, т. е. A x ^*= y или A B y = y, т. е. A B = I_Y.

3))1). Если существует правый обратный оператор B к оператору A, то для любого y Î Y точка x = B y является решением уравнения A x = y, так как A x = A (B y)= y. Лемма доказана.

Пример 2.1. Пусть A – оператор дифференцирования 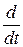: C ¹[0,1]® C [0,1]. Обычно говорят, что обратной к дифференцированию является операция интегрирования B : C [0,1]® C ¹[0,1], .

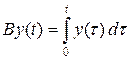Вычислим произведения:

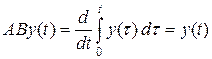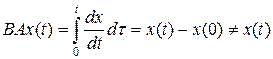Значит, A B = I, B A ¹ I и оператор интегрирования является правым обратным к оператору дифференцирования, но не является левым обратным.

Замечание 2.1. Существование линейных ограниченных обратных операторов связано с более тонкими свойствами. Для существования линейного ограниченного левого обратного к оператору A необходимо, чтобы образ Im A был дополняемым замкнутым линейным подпространством в Y, для существования линейного ограниченного правого обратного необходимо, чтобы подпространство Ker A имело дополнение в X.

В практических задачах функция y получается в результате измерений и, следовательно, с некоторой погрешностью, т. е. практически вместо точного решения x уравнения A x = y находим решение 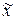приближенного уравнения A 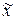=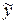. Может оказаться, что, несмотря на то, что 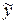близко к y, решение 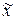сильно отличается от x. Расчеты (решение приближенного уравнения) имеют смысл только тогда, когда для близких y решения близки. Так как x = A ^–¹ y, 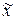= A ^–¹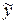, то требование непрерывной зависимости решения от правой части является фактически требованием непрерывности оператора
A ^–¹.

Уравнение A x = y называется корректно разрешимым, если 1) решение существует для любой правой части; 2) решение единственно; 3) решение непрерывно зависит от правой части.

Из предыдущих рассуждений следует, что корректная разрешимость уравнения A x = y эквивалентна существованию ограниченного обратного оператора A ^–¹. Заметим, что свойство корректной разрешимости существенно зависит от рассматриваемых пространств и норм на них.

Приведем несколько теорем, которые позволяют получить существование ограниченного обратного к оператору A.

Оператор A называется обратимым, если для него существует линейный ограниченный обратный оператор.

Теорема 2.1. Пусть X – банахово пространство, Y – нормированное пространство, A : X ® Y – ограниченный линейный оператор и пусть:

1) 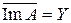(образ плотен в Y);

2) существует постоянная C >0 такая, что || A x ||³ C || x ||.

Тогда оператор A обратим.

Доказательство. Из условия 2) получаем, что если A x =0, то x =0, т. е. Ker A ={0}.

Проверим, что в действительности образ Im A замкнут и совпадает с Y. Пусть y Î Y и пусть y_n ® y, y_n ÎIm A, т. е. y_n = A x_n. Покажем, что y ÎIm A. Используя неравенство 2), получаем

|| x_n – x_m ||£(1/ C)|| A x_n – A x_m ||=(1/ C)|| y_n – y_m ||®0.

Значит, { x_n } – последовательность Коши в X и, в силу полноты пространства X, { x_n } сходится к некоторому элементу x Î X. Тогда ввиду непрерывности A имеем 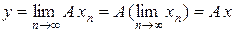, т. е. y ÎIm A. Таким образом, в силу лемм 2.1 и 2.2 существует обратный A ^–¹. Проверим, что он ограничен. Действительно, в силу неравенства 2)

|| A ^–¹ y ||£(1/ C)|| A (A ^–¹ y)||£(1/ C)|| y ||.

Теорема доказана.

Замечание 2.2. Несмотря на внешнюю сложность условий 1) и 2), в ряде задач их проверка легко осуществляется. Например, если уравнение A x = y рассматривается в пространстве функций на отрезке, то часто для функций, являющихся многочленами, решение строится в явном виде. Так как множество многочленов всюду плотно в ряде пространств, например в L_p [0,1], 1£ p <+¥, для этих пространств таким образом можем проверить условие 1). Неравенство из условия 2) в некоторых задачах, имеющих физический смысл, является следствием закона сохранения энергии. В связи с этим неравенства такого вида иногда называют энергетическими.

Замечание 2.3. Очевидно, что условия теоремы являются необходимыми для существования ограниченного обратного оператора.

Теорема 2.2. Пусть X – банахово пространство и A Î L (X), || A ||<1. Тогда оператор T = I – A обратим.

Доказательство. В случае, если A есть число и | A |<1, то число
(I – A)^–¹ является суммой бесконечной геометрической прогрессии
(I – A)^–¹=1+ A + A ²+¼ Покажем, что аналогичное равенство имеется и в случае, когда A есть оператор.

Рассмотрим в пространстве L (X) линейных ограниченных операторов ряд

I + A + A ²+¼ (2)

Докажем, что этот ряд сходится и его сумма есть обратный оператор к T. Так как || A ²||£|| A ||²,¼,|| Aⁿ ||£|| A || ⁿ,¼, то получаем мажорирующий сходящийся ряд

1+|| A ||+|| A ||²+¼=1/(1–|| A ||).

Так как пространство L (X) полно, то ряд (2) сходится (см. теорему 14.2 курса «Функциональный анализ. Часть 1»). Пусть S – его сумма, S_n = I + A +¼+ Aⁿ – частичная сумма. Тогда в силу непрерывности умножения

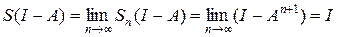Аналогично

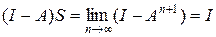Теорема доказана.

Замечание 2.4. Из доказательства имеем оценки

||(I – A)^–¹||£1/(1–|| A ||), || I –(I – A)^–¹||£|| A ||/(1–|| A ||).

Теорема 2.2 является некоторым усилением принципа сжимающих отображений для линейных операторов в банаховых пространствах. Решение уравнения x – A x = y (y – фиксированная точка) есть неподвижная точка отображения f (x)= A x + y. Отображение f является сжимающим тогда и только тогда, когда || A ||<1.

Теорема 2.3. Пусть X и Y – банаховы пространства и пусть оператор A Î L (X, Y) имеет ограниченный обратный. Если оператор B удовлетворяет условию || A – B ||<1/|| A ^–¹||, то оператор B имеет ограниченный обратный.

Доказательство. Рассмотрим произведение A ^–¹ B = A ^–¹[ A –(A – B)]=
= I – A ^–¹(A – B). Так как || A ^–¹(A – B)||£|| A ^–¹|||| A – B ||<1 по условию, то оператор I – A ^–¹(A – B) имеет ограниченный обратный в силу теоремы 2.2 и
{[ I – A ^–¹(A – B)]^–¹ A ^–¹} B = I, т. е. оператор, стоящий в фигурных скобках, является ограниченным левым обратным к оператору B. Аналогично, рассмотрев
B A ^–¹= I –(A – B) A ^–¹, получаем

B { A ^–¹[ I –(A – B) A ^–¹]^–¹}= I,

т. е. оператор B имеет правый ограниченный обратный. Тогда левый и правый обратные совпадают и у оператора B существует ограниченный обратный. Теорема доказана.

Следствие 2.1. Множество обратимых операторов в L (X, Y) есть открытое множество.

Доказательство. Теорема 2.3 утверждает, что у обратимого оператора A существует целая окрестность (шар радиуса 1/|| A ^–¹||), состоящая из обратимых операторов, т. е. по определению открытого множества в метрическом пространстве множество обратимых операторов открыто. Следствие доказано.

Следствие 2.2. Пусть A Î L (X, Y) – обратимый оператор (пространства X и Y – банаховы) и пусть A_n ® A по норме, где A_n Î L (X, Y). Тогда, начиная с некоторого номера n ₀, все операторы A_n обратимы и A_n ^–¹® A ^–¹ по норме.

Доказательство. Возьмем номер n ₀ так, чтобы при n ³ n ₀ выполнялось || A_n – A ||<1/|| A ^–¹||. Тогда по теореме 2.3 все операторы A_n при n ³ n ₀ обратимы. Оператор A_n ^–¹ имеет вид (из доказательства теоремы)

A_n ^–¹=[ I – A ^–¹(A – A_n)]^–¹ A ^–¹.

Так как 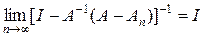(замечание к теореме 2), то в силу непрерывности умножения получаем, что A_n ^–¹® A ^–¹ по норме. Это утверждение, в частности, означает, что переход к обратному оператору как отображение, определенное на множестве обратимых операторов, является непрерывным. Следствие доказано.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

1 2 3 4 5 6 7

Подборка статей по вашей теме: