Пространства линейных ограниченных операторов

Лекция 1 Пространства линейных ограниченных операторов. Сильная сходимость последовательности операторов

1.1. Пространства линейных ограниченных операторов

1.2. Сильная сходимость последовательности операторов. Теорема
Банаха – Штейнгауза

Пусть X и Y – нормированные пространства. Рассмотрим множество L (X, Y), состоящее из всех линейных ограниченных операторов, действующих из X в Y.

Если A, B Î L (X, Y), то суммой A + B операторов A и B называется оператор, действующий по формуле

(A + B)(x) = A x + B x.

Произведением оператора A на число l называется оператор l A, действующий по формуле

(l A)(x) = l A x.

Напомним, что для ограниченного линейного оператора определена норма

.

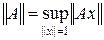Теорема 1.1. Множество L (X, Y) с введенными операциями сложения, умножения на число и нормой оператора образует нормированное линейное пространство. Пространство L (X, Y) полно, если полно пространство Y.

Доказательство. Проверим сначала, что введенные операции не выводят из множества L (X, Y). Если A, B Î L (X, Y), то

(A + B)(x ₁ + x ₂) = A (x ₁ + x ₂) + B (x ₁ + x ₂) = A x ₁ + A x ₂ + B x ₁ + B x ₂ = (A + B)(x ₁) + (A + B)(x ₂)

и, значит, A + B – аддитивный оператор,

(A + B)(l x) = A (l x) + B (l x) = l (A x) + l (B x) = l (A x + B x) = l (A + B)(x)

и, следовательно, A + B – однородный оператор. Аддитивность и однородность оператора l A доказывается аналогично.

Проверим, что A + B – ограниченный оператор. Действительно,

|| (A + B)(x) || = || A x + B x || £ || A x || + || B x || £ || A || || x || + || B || || x || = ( || A || + || B || ) || x ||.

Следовательно, оператор A + B ограниченный и || A + B || £ || A || + || B ||, т. е. для нормы оператора справедливо неравенство треугольника. Нулевой оператор (O x = 0) является нулевым элементом в линейном пространстве L (X, Y). Проверим остальные аксиомы нормы.

Если || A || = 0, то || A x || £ 0 || x ||, т. е. || A x || = 0 и, значит, A = O:

.

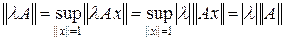Таким образом, L (X, Y) – нормированное пространство.

Пусть Y – банахово пространство. Докажем, что любая последовательность Коши { A_n } в пространстве L (X, Y) сходится. Возьмем x Î X и рассмотрим последовательность образов y_n = A_n x. Так как || y_n – y_m || = || (A_n –
– A_m)(x) || £ || A_n – A_m || || x || ® 0, то { y_n } – последовательность Коши в пространстве Y и, значит, существует предел 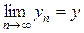. Определим оператор A, положив A x = y. Проверим, что построенный оператор линейный и ограниченный и что || A_n – A || ® 0.

Переходя к пределу в равенстве A_n (l ₁ x ₁ + l ₂ x ₂) = l ₁ A_n x ₁ + l ₂ A_n x ₂, получаем A (l ₁ x ₁ + l ₂ x ₂) = l ₁ A x ₁ + l ₂ A x ₂, т. е. A – линейный оператор. Так как последовательность Коши всегда ограничена, то существует постоянная C > 0 такая, что || A_n || £ C. Поэтому, переходя к пределу в неравенстве || A_n x || £ C || x ||, получаем || A x || £ C || x ||, т. е. A – ограниченный оператор. Возьмем e > 0 и найдем по нему n ₀ так, чтобы при n, m ³ n ₀ выполнялось || A_n – A_m || £ e. Тогда
|| A_n x – A_m x || £ e || x ||. Переходя в этом неравенстве к пределу при m ® ¥, получаем || A_n x – A x || £ e || x ||, т. е. для n ³ n ₀ имеем || A_n – A || £ e. Теорема доказана.

Будем говорить, что последовательность операторов { A_n } Ì L (X, Y) сходится к оператору A Î L (X, Y) по норме, если || A_n – A || ® 0.

Пусть оператор A действует из пространства X в пространство Y и оператор B действует из пространства Y в пространство Z. Произведением операторов A и B называется оператор (B A), определенный равенством (B A)(x) = B (A x).

Теорема 1.2. Пусть A Î L (X, Y), B Î L (Y, Z), где X, Y, Z – линейные нормированные пространства. Оператор B A является ограниченным линейным оператором из X в Z и || B A || £ || B || || A ||. Операция умножения операторов непрерывна относительно нормы, т. е. если A_n ® A и B_n ® B по норме, то A_n B_n ® A B по норме.

Доказательство. Линейность произведения линейных отображений очевидна. Для x Î X получаем

|| (B A)(x) || = || B (A x) || £ || B || || A x || £ || B || || A || || x ||,

т. е. для оператора B A выполнено неравенство ограниченности с постоянной || B || || A ||. Значит, || B A || £ || B || || A ||.

Оценим норму разности

|| B_n A_n – B A || = || B_n (A_n – A) + (B_n – B) A || £ || B_n || || A_n – A || + || B_n – B || || A ||.

Так как || A_n – A || ® 0 и || B_n – B || ® 0 и последовательность {|| B_n ||} ограничена, получаем || B_n A_n – B A || ® 0. Теорема доказана.

Рассмотрим следующий пример сходящейся последовательности операторов.

Пример 1.1. Пусть последовательность функций K_n (t, s), опреденных и непрерывных на квадрате [0, 1] ´ [0, 1], равномерно сходится к функции K (t, s). Тогда последовательность интегральных операторов Фредгольма в C [0, 1]

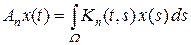
по норме сходится к интегральному оператору

.

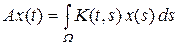Действительно, разность A_n – A есть интегральный оператор с ядром K_n (t, s) – K (t, s). Тогда

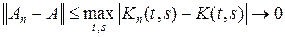
(см. пример 15.5 курса «Функциональный анализ. Часть 1»).

Пример 1.2. Пусть K (t, s) Î L ₂ ( [0, 1] ´ [0, 1] ), т. е. измеримая функция такая, что 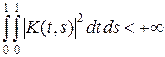. Выберем в пространстве L ₂[0, 1] базис e_j (t). Тогда, согласно теореме 18.5 курса «Функциональный анализ. Часть 1», функции e_{i j} = e_i (t) e_j (t) образуют базис в пространстве L ₂ ( [0, 1] ´ [0, 1] ). Разложим функцию K (t, s) в ряд по этой системе:

.

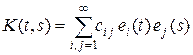Пусть 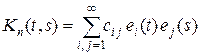. Покажем, что последовательность интегральных операторов

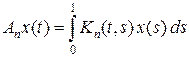
в пространстве L ₂[0, 1] сходится по норме к интегральному оператору

.

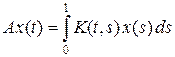Как и в примере 1.1, A_n – A есть интегральный оператор с ядром K_n (t, s) –
– K (t, s). Тогда

,

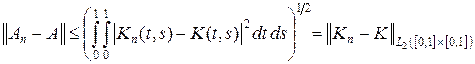(см. пример 15.8 курса «Функциональный анализ. Часть 1»), но так как K_n - частичные суммы ряда Фурье для функции K, то, по теореме 18.2 курса «Функциональный анализ. Часть 1» || K_n – K || ® 0 и, значит, || A_n – A || ® 0. Заметим, что здесь операторы K_n суть операторы конечного ранга, т. е. множество их значений – конечномерное подпространство.

Пример 1.3. Пусть операторы A_n в C [0, 1] имеют вид A_n x (t) = a_n (t) x (t), где a_n (t) – непрерывная функция, и пусть последовательность функций { a_n (t)} равномерно на [0, 1] сходится к функции a (t). Тогда последовательность оператров A_n x (t) = a_n (t) x (t) сходится по норме к оператору A x (t) = a (t) x (t). Действительно,

.

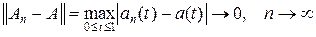Пример 1.4. Пусть функция K (t, s) определена для 0 £ t £ l, 0 £ s £ l и имеет вид

K (t, s) = K ₀ (t, s) | t – s | ^{– g},

где 0 < g < l и функция K ₀ (t, s) непрерывна, т. е. K (t, s) – слабополярное ядро (см. определение 15.4 курса «Функциональный анализ. Часть 1»).

Покажем, что в пространстве C [0, 1] интегральный оператор A со слабополярным ядром K (t, s) является пределом последовательности интегральных операторов K_n с непрерывными ядрами. Для этого построим непрерывные функции

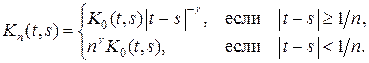
И пусть A_n – интегральный оператор с ядром K_n (t, s). Тогда

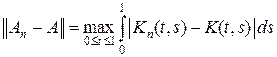
(см. пример 15.6 курса «Функциональный анализ. Часть 1»). Функция K ₀ (t, s) непрерывна на компактном множестве и, следовательно, ограничена некоторой постоянной C.

Оценим интеграл

.

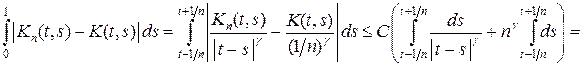
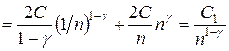Так как g < 1, показатель 1 – g положительный и получаем, что

|| A_n – A || £ C ₁ / n ^{1 – g} ® 0 при n ® + ¥.