Пучок прямых

Определение. Собственным пучком прямых называют множество всевозможных прямых на плоскости, проходящих через данную точку (называемую центром пучка).

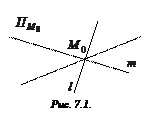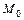Пусть – центр пучка (известен).

Пусть 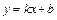– уравнение .

Т.к. 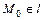, то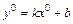

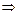
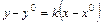. (6.1)

(6.1) – уравнение пучка (прямой, проходящей через данную точку ).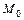

2) Пусть центр пучка неизвестен. Есл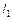и 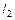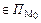и и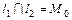

()

()

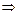
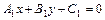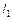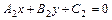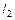и .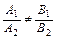

Тогда уравнение

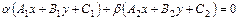(6.2)

при условии

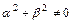(6.3)

определяет некоторую прямую из 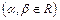, и, следовательно, является уравнением пучка прямых.

Действительно, соотношение (6.2)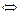

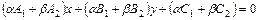, (6.4)

т.е. является уравнением вида 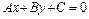, т.е уравнением некоторой прямой , причем .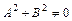

(Если 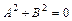, то это означает, что 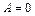и 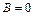, т.е. справедлива система соотношений

,

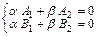которая в силу условия (6.3) обязана иметь ненулевое решение. А это означает, что определитель этой системы должен быть равен нулю:

.

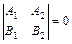А это равносильно условию

,

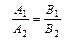и, следовательно, 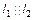. Получили противоречие. Значит, действительно 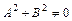и уравнение (6.2) определяет прямую).

Кроме того, если 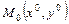– точка пересечения прямых 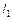и 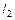, т.е. центр пучка, то 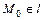, т.к.

,

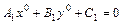
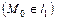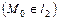
и поэтому

,

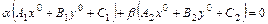следовательно, .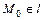

Замечание: Уравнение (6.2) зависит не от самих 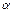и 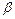, а от их отношения.

Если 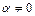, то (6.2) при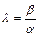

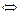
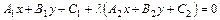. (6.5)

Соотношение (6.5) – уравнение прямой собственного пучка.

Если 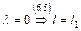, если же .

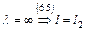Определение. Несобственным пучком прямых называют множество всевозможных прямых плоскости, параллельных некоторой прямой.

Пусть прямая ()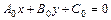

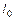определяет несобственный пучок прямых и ()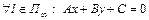

Т. к. 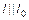, то

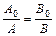
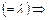
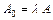и . (*)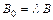

Умножим теперь обе части уравнения прямой на :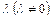

.

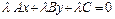В силу соотношений (*) при 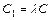получаем

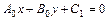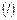. (6.6)

Таким образом, если прямая 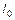задана общим уравнением и определяет несобственный пучок прямых, то уравнение произвольной прямой этого пучка, не совпадающей с прямой 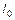, отличается от уравнения прямой 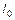только значением свободного члена.