Операционное исчисление широко используется в физике, механике, электротехнике, автоматике, телемеханике и т.д. Основоположником операционного исчисления считают английского инженера-электрика О. Хевисайда (1850 – 1925).
Преобразование Лапласа
Пусть функция f (t) действительной переменной t, определённая при t ≥ 0 (при −∞ < t < +∞, берут f (t) = 0 при t < 0), кусочно непрерывная, т.е. в любом конечном интервале она имеет конечное число точек разрыва 1-го рода.
Для обеспечения существования некоторых интегралов в бесконечном интервале 0 < t < +∞ наложим на функцию f (t) дополнительное условие: пусть существует число М > 0 и s 0 > 0 такие, что
| f (t)| < М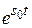 (1)
(1)
при любом t 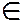 [0, +∞); число s 0 − показатель роста функции f (t).
[0, +∞); число s 0 − показатель роста функции f (t).
Рассмотрим функцию
е−рtf (t), (2)
где р = а + ib (a > 0 или Re p > 0) – некоторое комплексное число.
Тогда функция (2) является комплексной функцией действительной переменной t:
е−рtf (t) = е− ( a + ib ) tf (t) = е−atf (t) е−ibt =
= е−atf (t)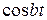 − iе−atf (t)
− iе−atf (t)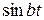 .
.
Рассмотрим несобственный интеграл:
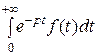 =
= 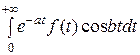 − i
− i 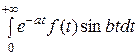 . (3)
. (3)
Если f (t) удовлетворяет условию (1) и a > s 0, то интегралы, стоящие в правой части (3), существуют и абсолютно сходятся.
Действительно, оценим 1-ый интеграл:
|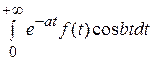 | ≤
| ≤ 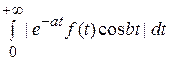 < M
< M 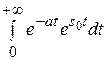 = M
= M 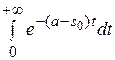 =
=
= 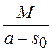 ,
,
т.е. интеграл сходится абсолютно.
Аналогично оценивается 2-ой интеграл. Итак, 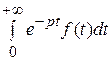 существует. Он определяет некоторую функцию от р, которую обозначим F (p):
существует. Он определяет некоторую функцию от р, которую обозначим F (p):
F (p) = 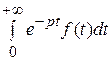 . (4)
. (4)
Функция F (p) – функция комплексного переменного и она является аналитической в полуплоскости Re p > s 0:
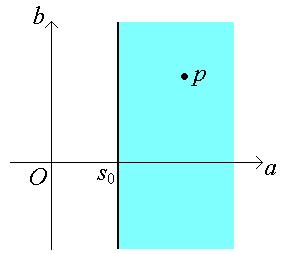
Функция F (p) называется изображением Лапласа функции f (t), L - изображением, просто изображением функции f (t) или преобразованием Лапласа.
Функцию f (t) называют начальной функцией или оригиналом.
Если F (p) есть изображение функции f (t), то будем писать:
F (p)  f (t)
f (t)
или
f (t)  F (p),
F (p),
или
L { f (t)} = F (p).
Процесс нахождения изображения для заданного оригинала и обратно, нахождение оригинала по известному изображению называется операционным исчислением.
Теорема единственности. Если две непрерывные функции φ (t) и ψ (t) имеют одно и то же L −изображение F (p), то эти функции тождественно равны.
Из теоремы следует: если при решении практической задачи найдено изображение искомой функции, а потом по изображению найдена сама функция, то она единственная.
Изображения простейших функций
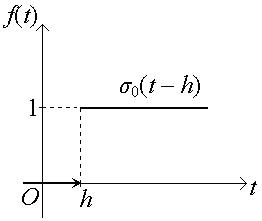
1. Функцию
f (t) = 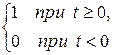
называют единичной функцией Хевисайда и обозначают σ 0(t):
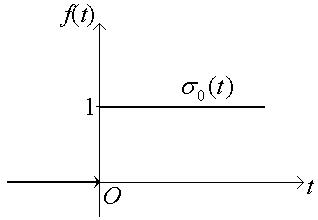
Очевидно, что показатель роста этой функции s 0 = 0. Найдем L -изображе-
ние этой функции в области Re p > 0:
L { σ 0(t)} =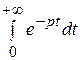 =
= 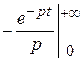 =
= 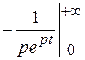 =
= 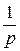 .
.
Таким образом,
1 
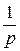 или σ 0(t)
или σ 0(t) 
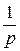 . (5)
. (5)
2. f (t) = 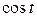 .
.
L {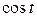 } =
} =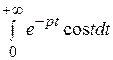 =
= 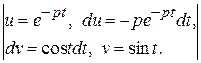 =
= 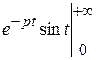 +
+
+ p 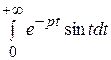 = p
= p 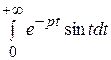 =
= 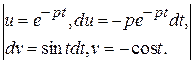 = p (−
= p (−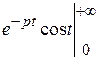 −
−
− p 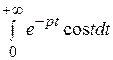 ) = p − p 2 L {
) = p − p 2 L {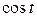 }.
}.
Отсюда
L {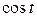 } =
} = 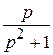 (Re p > 0), т.е.
(Re p > 0), т.е.
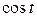

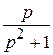 . (6)
. (6)
3. f (t) = 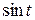 .
.
При выводе формулы (6) мы получили
L {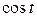 } = p
} = p 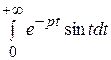 , т.е. L {
, т.е. L {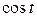 } = р L {
} = р L {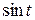 }. Откуда
}. Откуда
L {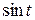 } =
} = 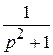
или
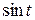

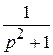 . (7)
. (7)
Изображение функции f (αt)
Теорема подобия. Если
f (t)  F (p), то
F (p), то
f (αt) 
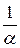 F (
F (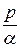 ) (8)
) (8)
(α > 0, Re p > 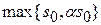 ).
).
○ Найдем изображение функции f (αt):
L { f (αt)}=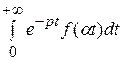 =
= 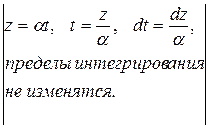 =
= 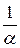
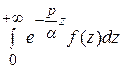 =
= 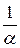 F (
F (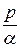 ), т.е.
), т.е.
f (αt) 
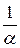 F (
F (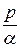 ). ●
). ●
Пусть f (αt) = 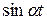 . Если
. Если
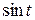

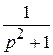 , то
, то 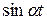

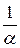 ∙
∙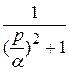 или
или
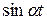

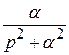 . (9)
. (9)
Пусть f (αt) = 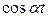 . Если
. Если
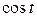

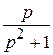 , то
, то 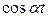

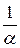 ∙
∙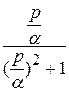 или
или
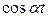

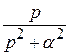 . (10)
. (10)
Свойство линейности
Теорема. Изображение суммы нескольких функций, умноженных на постоянные, равняется сумме изображений этих функций, умноженных на соответствующие постоянные, т.е. если
f (t) = 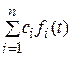 (сi = const) (*)
(сi = const) (*)
и
F (p)  f (t), Fi (p)
f (t), Fi (p)  fi (t),
fi (t),
то
F (p) = 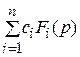 . (11)
. (11)
○ Умножая все члены равенства (*) на е−рt и интегрируя по t в пределах от 0 до +∞ (вынося множители сi за знак интеграла), получим
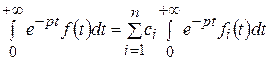 ,
,
но
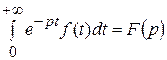 и
и 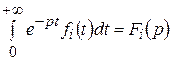
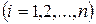 .
.
Тогда 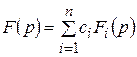 . ●
. ●
Пример. Найти изображение функции
f (t) = 3 σ 0(t) + 2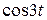 .
.
□
В силу (5), (10) и (11) имеем
L { f (t)} = 3 L { σ 0(t)} + 2 L {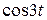 } =
} = 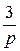 +
+ 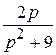
или
F (p) = 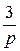 +
+ 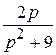 .
.
■
Пример. Найти оригинал изображения
F (p) = 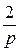 +
+ 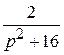 .
.
□
Представим изображение в виде
F (p) = 2∙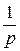 +
+ 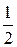 ∙
∙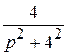 .
.
Имеем
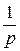
 σ 0(t),
σ 0(t), 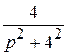

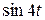 .
.
Следовательно, оригинал
f (t) = 2 σ 0(t) + 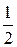
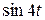
или
f (t) = 2 + 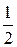
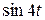 .
.
■
Теорема смещения
Теорема. Если
F (p)  f (t),
f (t),
то
F (p + α)  е−αt f (t) (12)
е−αt f (t) (12)
(Re (p + α) > s 0).
○ Найдем изображение функции е−αtf (t):
L { е−αtf (t)} =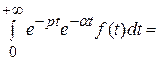
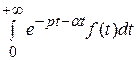 =
=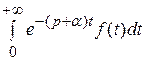 = F (p + α),
= F (p + α),
т.е.
F (p + α)  е−αt f (t). ●
е−αt f (t). ●
Доказанная теорема позволяет значительно расширить класс изображений, для которых легко находятся начальные функции.
Так как 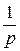
 1, то по формуле (12)
1, то по формуле (12)
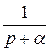
 е−αt (13)
е−αt (13)
и
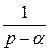
 еαt. (
еαt. (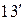 )
)
Вычтем из (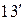 ) равенство (13) и разделим на 2:
) равенство (13) и разделим на 2:
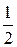 (
(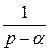 −
− 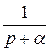 )
) 
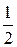 (еαt − е−αt)
(еαt − е−αt)
или
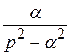
 Sh αt. (14)
Sh αt. (14)
Сложим (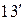 ) с (13) и разделим на 2:
) с (13) и разделим на 2:
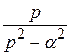
 Сh αt. (15)
Сh αt. (15)
Так как 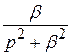

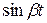 , то
, то
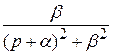
 е−αt
е−αt 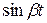 . (16)
. (16)
Так как 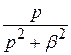

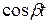 , то
, то
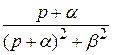
 е−αt
е−αt 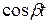 . (17)
. (17)
Пример. Найти начальную функцию, изображение которой задается функцией
F (p) = 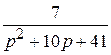 .
.
□
Преобразуем F (p):
F (p) = 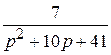 =
= 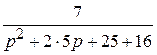 =
= 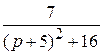 =
= 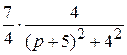 .
.
Следовательно, согласно (16):
F (p) 
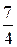 е− 5 t
е− 5 t 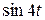
или
f (t) = 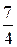 е− 5 t
е− 5 t 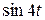 .
.
■
Пример. Найти оригинал изображения
F (p) = 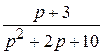 .
.
□
Преобразуем изображение:
F (p) = 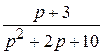 =
= 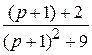 =
= 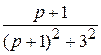 +
+ 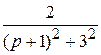 =
= 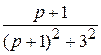 +
+
+ 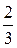 ∙
∙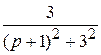 .
.
Следовательно,
F (p)  е−t
е−t 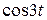 +
+ 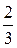 е−t
е−t 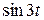
или
f (t) = е−t 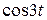 +
+ 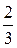 е−t
е−t 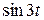 .
.
■
Дифференцирование изображения
Теорема. Если
F (p)  f (t),
f (t),
то
(−1) п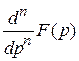
 tn f (t) (18)
tn f (t) (18)
или
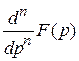
 (− t) n f (t) (1
(− t) n f (t) (1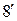 )
)
○ Если Re p > s 0, где s 0 – роста функции f (t), то интеграл
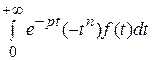
существует при любом п = 1, 2, ….
Но этот интеграл можно рассматривать как производную п -го порядка по параметру р от интеграла
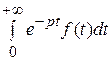 .
.
Например, при п = 1:
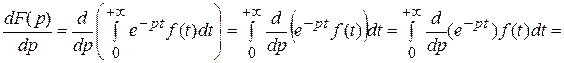
= 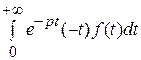 .
.
Таким образом,
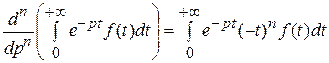
или
(−1) п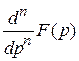 =
= 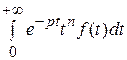 .
.
Окончательно,
(−1) п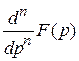
 tn f (t). ●
tn f (t). ●
Пример. Известно, что 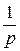
 1. Найти изображение функции tn.
1. Найти изображение функции tn.
□
На основании (18)
при п = 1:
(−1) 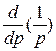
 t или
t или 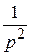
 t;
t;
при п = 2:
(−1)2 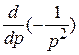
 t 2, −(−
t 2, −(−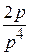 )
)  t 2
t 2
или
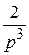
 t 2;
t 2;
при п = 3:
(−1)3 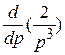
 t 3, −(−
t 3, −(−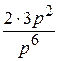 )
)  t 3
t 3
или
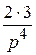
 t 3.
t 3.
Тогда для произвольного п:
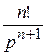
 tп. (19)
tп. (19)
Пример. Известно, что 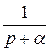
 е−αt. Найти изображение функции tе−αt.
е−αt. Найти изображение функции tе−αt.
□
На основании (18) при п = 1:
(−1) 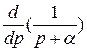
 tе−αt
tе−αt
или
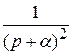
 tе−αt.
tе−αt.
■
Дифференцирование оригинала
(изображение производных)
Теорема. Если
F (p)  f (t),
f (t),
то
р F (p) − f (0) 
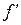 (t) (20)
(t) (20)
(Re p > s 0).
При этом предполагается, функция f (t) непрерывна, имеет кусочно-непрерывную производную 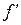 (t) на [0, +∞) c разрывами первого рода и показатели роста
(t) на [0, +∞) c разрывами первого рода и показатели роста 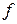 (t) и
(t) и 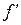 (t) равны s 0.
(t) равны s 0.
○ По определению изображения
L {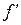 (t)} =
(t)} =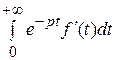 =
=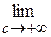
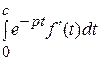 =
= 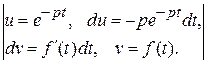 =
=
=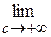 (е−рtf (t)
(е−рtf (t) 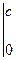 + p
+ p 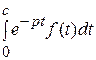 ) = − f (0) + pF (p) (Re p > s 0),
) = − f (0) + pF (p) (Re p > s 0),
потому что
| е−рcf (c) | ≤ е−рcM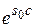 = M
= M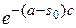
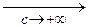 0.
0.
Таким образом,
р F (p) − f (0) 
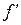 (t). ●
(t). ●
Следствие. Справедлива формула изображения для производной п -го порядка:
pпF (p) − pп −1 f (0) − pп −2 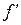 (0) − …− pf ( n −2)(0) − f ( n −1)(0)
(0) − …− pf ( n −2)(0) − f ( n −1)(0)  f ( n )(t). (21)
f ( n )(t). (21)
○ Пусть
φ (t) = 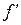 (t) и Φ (p)
(t) и Φ (p)  φ (t) =
φ (t) = 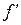 (t). В то же время
(t). В то же время
рF (p) − f (0) 
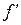 (t),
(t),
следовательно,
Φ (p) = рF (p) − f (0).
Найдем изображение функции
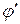 (t) =
(t) = 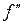 (t):
(t):
рΦ (p) − φ (0) 
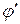 (t) =
(t) = 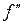 (t).
(t).
Значит,
р (рF (p) − f (0)) − 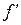 (0)
(0) 
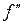 (t)
(t)
или
p 2 F (p) − pf (0) − 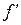 (0)
(0) 
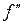 (t)
(t)
и т.д. ●
Замечание. Если
f (0) = 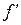 (0) = … = f ( n −1)(0) = 0,
(0) = … = f ( n −1)(0) = 0,
то
pпF (p)  f ( n )(t).
f ( n )(t).
Пример. Найти изображение функции
f (t) = 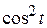 .
.
□
Пусть F (p) 
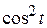 = f (t). Тогда
= f (t). Тогда
рF (p) − f (0) 
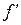 (t).
(t).
Но
f (0) = 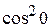 = 1,
= 1,
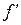 (t)=−2
(t)=−2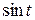
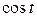 = −
= −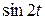
 −
−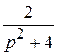 .
.
Следовательно,
рF (p) − 1 = −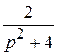 ,
,
откуда
F (p) = 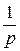 (1 −
(1 − 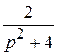 ) =
) = 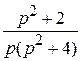 .
.
■
Интегрирование оригинала
Теорема. Если
F (p)  f (t),
f (t),
то
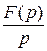

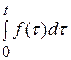 . (22)
. (22)
Пример. Найти изображение функции
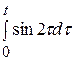 .
.
□
Имеем
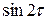

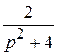 .
.
По теореме об интегрировании оригинала
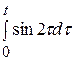

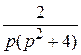 .
.
■
Интегрирование изображения
Теорема. Если интеграл
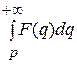
сходится, то он является изображением функции
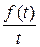 ,
,
т.е. 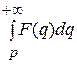

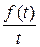 . (23)
. (23)
Следствие.
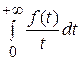 =
= 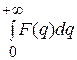 , (24)
, (24)
если сходятся соответствующие несобственные интегралы.
Пример. Найти изображение функции
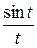 .
.
□
Известно, что 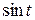

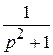 . Поэтому по теореме об интегрировании изображения
. Поэтому по теореме об интегрировании изображения
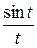

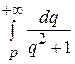 =
=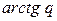
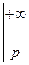 =
=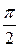 −
−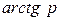 ,
,
т.е.
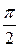 −
− 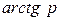

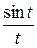 .
.
■
Пример. Найти интеграл
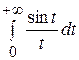 .
.
□
Используя предыдущий пример и последнее следствие, получим
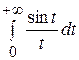 =
=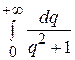 =
= 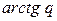
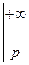 =
= 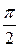 .
.
■
Запаздывание оригинала
Теорема. Пусть f (t) > 0 при t < 0, тогда
L { f (t – t 0} = 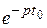 L { f (t)}, (25)
L { f (t)}, (25)
где t 0 – некоторая точка.
○ Имеем
L { f (t – t 0} = 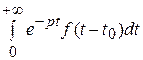 =
= 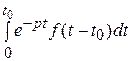 +
+ 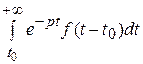 =
=
=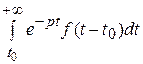 =
= 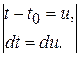 =
= 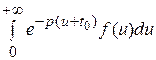 =
= 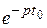
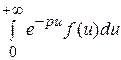 =
=
= 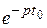 L { f (u)}. ●
L { f (u)}. ●
Пример. Так как
L { σ 0(t)} = 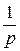 ,
,
то
L { σ 0(t – h)} = 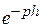
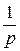
 ■
■
Решение дифференциальных уравнений операционным методом
Пусть дано линейное дифференциальное уравнение п -го порядка с постоянными коэффициентами
апх (п)(t) + ап −1 х (п −1)(t) + … + а 1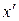 (t) + а 0 х (t) = f (t). (1)
(t) + а 0 х (t) = f (t). (1)
Требуется найти решение уравнения (1) для t > 0 при начальных условиях
х (0) = х 0, 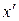 (0) =
(0) = 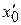 , …, х (п- 1)(0) = х 0(п- 1). (2)
, …, х (п- 1)(0) = х 0(п- 1). (2)
Другими словами, требуется решить задачу Коши.
Предположим, что функция х (t) является решением (1), удовлетворяющее начальным условиям (2). Тогда после подстановки этой функции в (1) мы получим тождество. Значит, функция, стоящая в левой части (1), и функция f (t) имеют одно и то же L -изображение:
L {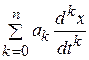 } = L { f (t)}.
} = L { f (t)}.
В силу следствия теоремы о дифференцировании оригинала имеем
L {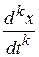 } = pkL { х }− pk −1 x (0) − … − p х ( k- 2)(0) − х ( k- 1)(0).
} = pkL { х }− pk −1 x (0) − … − p х ( k- 2)(0) − х ( k- 1)(0).
Поэтому, используя свойство линейности изображения, получим
апL {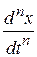 }+ ап- 1 L {
}+ ап- 1 L {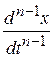 }+…+ а 0 L { х } = L { f (t)}:
}+…+ а 0 L { х } = L { f (t)}:
ап (pпL { х } − pп −1 x 0 − …− p х 0(п- 2) − х 0(п- 1)) + ап- 1(pп- 1 L { х } − pп −2 x 0 −…− pх 0(п- 3) − х 0(п- 2)) +
+…+ а 1(L { х }− x 0) + а 0 L { х } = L { f (t)}.
Введем обозначения:
L { х } = 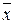 (р), L { f (t)} = F (p).
(р), L { f (t)} = F (p).
Тогда
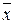 (р)∙(апpп + ап- 1 pп- 1 +…+ а 1 p + а 0) = ап (pп −1 x 0 + pп −2
(р)∙(апpп + ап- 1 pп- 1 +…+ а 1 p + а 0) = ап (pп −1 x 0 + pп −2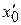 +…+ х 0(п- 1)) +
+…+ х 0(п- 1)) +
+ ап- 1(pп −2 x 0 + pп −3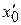 +…+ х 0(п- 2)) +… + а 2(px 0 +
+…+ х 0(п- 2)) +… + а 2(px 0 + 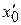 ) + а 1 x 0 + F (p). (3)
) + а 1 x 0 + F (p). (3)
Уравнение (3) называют вспомогательным уравнением или изображающим уравнением, или операторным уравнением.
Видно, что коэффициент при 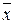 (р) в (3) получается из левой части (1) формальной заменой производных
(р) в (3) получается из левой части (1) формальной заменой производных 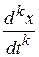 на степени pk. Обозначим этот коэффициент через
на степени pk. Обозначим этот коэффициент через
Rn (p) = (апpп + ап- 1 pп- 1 +…+ а 1 p + а 0).
Очевидно, что этот коэффициент является левой частью характеристического уравнения для дифференциального уравнения (1).
Правую часть уравнения (3), кроме F (p), обозначим через Ψп- 1(р):
Ψп- 1(р) = ап (pп −1 x 0 + pп −2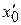 +…+ х 0(п- 1)) + ап- 1(pп −2 x 0 + pп −3
+…+ х 0(п- 1)) + ап- 1(pп −2 x 0 + pп −3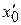 +…+ х 0(п- 1)) +…
+…+ х 0(п- 1)) +…
…+ а 2(px 0 +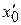 ) + а 1 x 0.
) + а 1 x 0.
Тогда уравнение (3) примет вид:
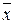 (р)∙ Rn (p) = F (p) +
(р)∙ Rn (p) = F (p) + 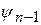 (р)
(р)
или
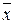 (р) =
(р) = 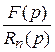 +
+ 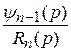 . (4)
. (4)
Если начальные условия нулевые, т.е.
х 0 =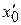 = … = х 0(п- 1) = 0,
= … = х 0(п- 1) = 0,
то формула (4) запишется
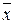 (р) =
(р) = 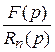 . (
. (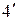 )
)
Если теперь по изображению (4) или (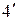 ) мы найдем оригинал, то в силу теоремы единственности это и будет искомое решение х (t).
) мы найдем оригинал, то в силу теоремы единственности это и будет искомое решение х (t).
Пример. Решить уравнение
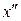 + 4 х = 2, х (0) =
+ 4 х = 2, х (0) =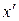 (0) = 0 или х 0 =
(0) = 0 или х 0 =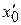 = 0.
= 0.
□
Так как начальные условия нулевые, то используем формулу (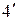 ). Имеем
). Имеем
2 
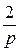 = F (p), R 2(p) = р 2 + 4.
= F (p), R 2(p) = р 2 + 4.
Следовательно,
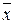 (р) =
(р) = 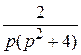 .
.
Разложим изображение на простейшие дроби:
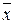 (р) =
(р) = 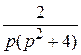 =
= 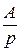 +
+ 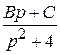 =
= 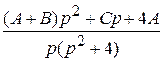 =!
=!
2 = (А + В) р 2 + Ср + 4 А,
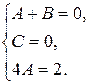
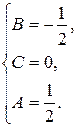 .
.
! = 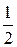 ∙
∙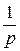 −
− 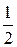 ∙
∙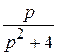 .
.
Следовательно,
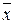 (р) =
(р) = 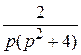 =
= 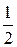 ∙
∙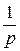 −
− 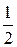 ∙
∙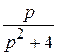

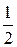 −
− 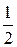 ∙
∙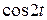 ,
,
т.е.
х (t) = 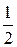 −
− 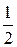 ∙
∙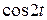 .
.
■
Пример. Решить уравнение
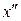 +
+ 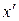 − 2 х = 0, х 0 = 1,
− 2 х = 0, х 0 = 1, 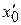 = 0.
= 0.
□
Имеем
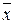 (р)
(р)  х (t), р
х (t), р 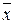 (р) – х 0
(р) – х 0 
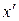 (t),
(t),
р 2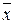 (р) – рх 0 −
(р) – рх 0 − 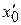

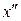 (t).
(t).
Подставляем в уравнение с учетом начальных условий
р 2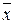 (р) – р + р
(р) – р + р 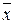 (р) – 1− 2
(р) – 1− 2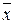 (р) = 0,
(р) = 0,
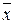 (р)(р 2 + р − 2) = р + 1,
(р)(р 2 + р − 2) = р + 1,
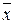 (р) =
(р) = 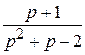 .
.
Разложим изображение на простейшие дроби:
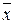 (р) =
(р) = 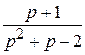 =
= 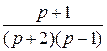 =
=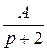 +
+ 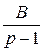 =
= 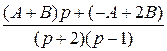 =!
=!
р + 1 = (А + В) р + (− А + 2 В),
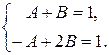
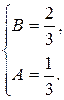 .
.
! = 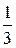 ∙
∙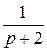 +
+ 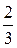 ∙
∙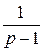 .
.
Следовательно,
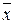 (р) =
(р) = 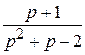 =
= 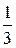 ∙
∙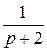 +
+ 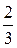 ∙
∙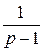

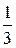 e− 2 t +
e− 2 t + 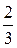 et,
et,
т.е.
х (t) = 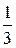 e− 2 t +
e− 2 t + 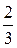 et.
et.
■
Нахождение оригиналов для рациональных дробей
При решении дифференциальных уравнений операционным методом мы столкнулись с определением решения ДУ (определением оригинала) от рациональных дробей, выражающих изображение.
Пусть изображение некоторой функции есть правильная рациональная дробь. Всякую правильную рациональную дробь можно представить в виде простейших (элементарных) дробей четырех видов:
1. 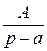 ;
;
2. 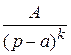 , где k – кратность корня;
, где k – кратность корня;
3. 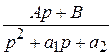 , где корни знаменателя комплексные, т.е.
, где корни знаменателя комплексные, т.е. 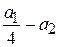 < 0;
< 0;
4. 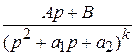 , где k ≥ 0, корни знаменателя комплексные.
, где k ≥ 0, корни знаменателя комплексные.
Запишем для этих дробей оригиналы.
1. 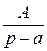
 Аeat.
Аeat.
Здесь использованы: формула 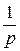
 1, свойство линейности и теорема смещения: F (p + α)
1, свойство линейности и теорема смещения: F (p + α)  е−αt f (t).
е−αt f (t).
2. 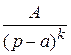

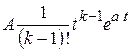 .
.
Соотношение получено на основании теоремы о дифференцировании изображения (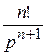
 tп) и теоремы смещения (F (p + α)
tп) и теоремы смещения (F (p + α)  е−αt f (t)):
е−αt f (t)):
из формулы 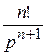
 tп следует
tп следует
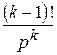
 tk− 1,
tk− 1, 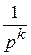

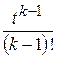 ,
, 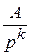

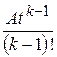 .
.
С учетом теоремы смещения:
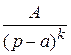

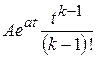 .
.
3. Рассмотрим дробь 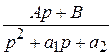 .
.
Произведем тождественные преобразования:
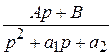 =
= 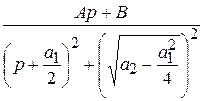 =
= 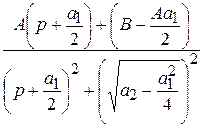 =
=
= 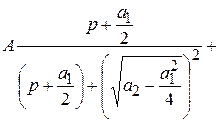
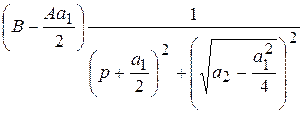 =
=
= 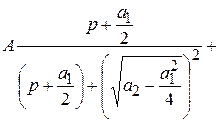
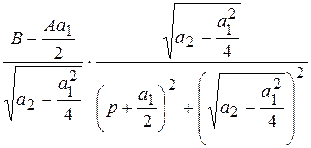 .
.
Тогда для первого слагаемого
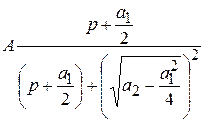

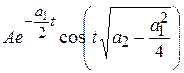 .
.
Здесь использованы: соотношение 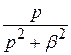

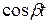 и теорема смещения F (p + α)
и теорема смещения F (p + α)  е−αt f (t).
е−αt f (t).
Используя соотношен
 2014-02-09
2014-02-09 3198
3198