Упругие механические элементы

Упругие механические элементы, используемые в сенсорных и актюаторных МЭМП и НЭМП, представляют собой обычно упругие балочные элементы – консольные балки (кантилеверы) или закрепленные по обоим концам балки (мостиковые структуры) и, хотя и значительно реже, закрепленные по периметру упругие мембраны. Все эти элементы изготавливаются из жестких материалов различной природы, которые должны обладать требуемыми механическими, электрическими и магнитными свойствами. Поскольку производство МЭМП и НЭМП базируется преимущественно на кремниевой технологии на практике чаще всего используются моно- и поликристаллический нелегированный и легированный кремний, его оксиды и нитриды различного состава, другие соединения и модификации, а также различные, в том числе рассмотренные в предыдущем разделе «умные» металлы, керамики, полимеры и их комбинации (биморфные, композиционные или гибридные структуры). Выбор материалов для таких элементов, их геометрическая форма и размеры диктуются как требованиями к конструкции и свойствам преобразователей, так и, в значительно больей степени, к технологии их изготовления.

Упругие механические элементы могут работать как в статических, так и в динамических режимах, т.е. вести себя как квазистатические, так и колебательные системы (резонаторы). Анализу особенностей их поведения и проявления масштабных эффектов в этих режимах посвящен данный раздел.

3.1.1. Поведение упругих механических элементовпри статических воздействиях

Физической основой действия упругих механических элементов в статических условиях является возникновение упругих (обратимых и линейных) изменений геометрических размеров (деформаций) 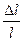, пропорциональных приложенной силе F_y при заданной площади А: 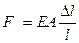. Из самого общего скейлингового (масштабного) анализа этого соотношения следует, что масштабный коэффициент упругой силы равен 2, т.е. изменение силы, при заданном коэффициенте пропорциональности (модуле упругости материала) Е, пропорционально квадрату произвольно выбранного линейного масштабного параметра [ L² ].

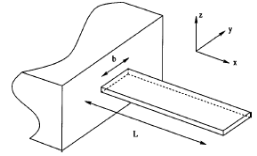
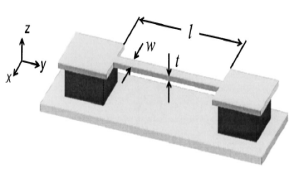
Конкретным взаимосвязям между силой и деформациями в закрепленных с одного (консольных) и с обоих концов (мостиковых) упругих балок (Рис.23 а) и б) соответственно) в зависимости от размеров и свойств материалов в статических условиях посвящен данный подраздел.

a) б)

Рис.23. Схематическое изображение консольной балки (а) и мостиковой структуры (б) длиной l, шириной в и толщиной а в координатах x-y-z.

Статический изгиб тонких балок описывается в общем виде уравнением Эйлера-Бернулли: 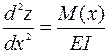, где x, z – соответственно, направления вдоль нейтральной оси в плоскости пластины (x-y) и перпендикулярно ей; М(х) – изгибающий момент как функция координаты х; Е – модуль Юнга материала балки; I – момент инерции поперечного сечения балки (при прямоугольном сечении балки высотой а и шириной в: 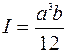; при круглом сечении радиусом r: ).

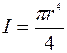При приложении силы F к свободному концу закрепленной с одного края (консольной) балки длиной l, т.е. в точке с координатой х = l, смещение нейтральной плоскости балки вдоль оси z относительно исходного ее положения при отсутствии силы как функция х: 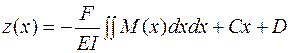, где С и D – константы интегрирования. При граничных условиях z(х = l) = 0: .

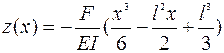Максимальное смещение (прогиб) свободного конца балки (х = l): 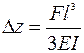. Соответственно, для балок прямоугольного и круглого сечения: 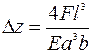и 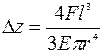. При наличии прикрепленной к концу балки точечной массы m, на которую действует ускорение g, прогиб балки определяется силой F=mg.

При приложении к консольной балке длиной l распределенной силы F=Wl, где W - удельная сила, равная F/l, и при граничных условиях z(х = l)=0: 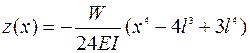. Максимальное смещение свободного конца балки (х =0): 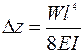. Соответственно, для балок прямоугольного и круглого сечения: 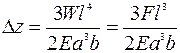и .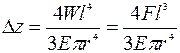

Примером распределенной силы может служить инерционная сила, действующая на балку при ускорении g. Для балки прямоугольного сечения: , где V – объем балки, ρ – плотность материала, ρV – масса балки. Тогда максимальное смещение конца такой балки, при отсутствии прикрепленной массы: 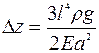. Следует обратить внимание, что при этом ширина балки не играет никакой роли.

Другим важным примером распределенной силы служит сила тяжести массы М, равномерно распределенной по поверхности балки: 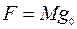, где g₀ – ускорение силы тяжести. Максимальный прогиб такой балки на ее конце: 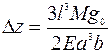. При просвете между балкой и ниже лежащей плоскостью h₀ максимальное смещение конца балки не может превышать эту величину.

Связь прогиба балок Δz с действующей силой F может быть также описана через коэффициент упругости пружины, или поперечную жесткость балки k_Z (F=k_ZΔz). Величина k_z определяется, в первую очередь, геометрией (длиной l и моментом инерции сечения I) балки, а также модулем упругости материала: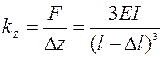, где Δl – удаление точки приложения силы от свободного конца балки. При приложении силы к свободному концу балки Δl =0. Соответственно, для балок прямоугольного и круглого сечения: 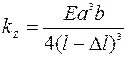и 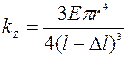. Если распределенная сила приложена к консольной балке на часть ее длины от свободного конца l_p, то ее жесткость может быть рассчитана по соотношению [5v#10]: 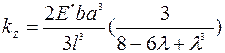, где: λ=l_p/l, Е* - эффективный модуль упругости, равный Е материала балки при а≈в и Е/(1-ν²) при в>5а, ν –коэффициент Пуассона.

При продольном кручении балки под действием крутящего момента М(x) упругость консольной балки характеризуется двумя упругими константам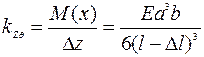и: и 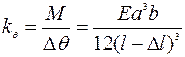, где Δz - прогиб балки по оси z, Δθ - поворот балки относительной малой оси.

При кручении консольной балки крутящим моментом Т вдоль главной оси х максимальный угол закрутки свободного конца балки Δφ равен: 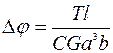, где С – константа, зависящая от отношения а/в и изменяющаяся от 0,1406 до 0,333 при изменении этого отношения от 1 до ∞. Упругая константа при этом равна: 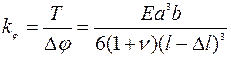, где ν – коэффициент Пуассона материала балки.

Для жестко закрепленной по обоим концам балки (мостиковой структуры) прямоугольного сечения при аналогичных размерах и силе, действующей на середину балки между опорам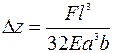и: и .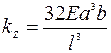

Для тонких мембран применение классических методов анализа с использованием уравнений движения, как в случае балок, требует определения координат пластины по осям х и y с учетом всех сдвиговых и изгибающих сил, что приводит к системе шести уравнений с шестью неизвестными. Кроме того, эмпирически установлено, что расчетные данные при этом плохо согласуются с экспериментально определенными. Поэтому на практике используется упрощенный подход, в котором сначала определяется соотношение между прогибом мембраны в центре w₀ и приложенным давлением p. Для квадратной мембраны толщиной а и шириной в, закрепленной по периметру, это соотношение имеет вид: 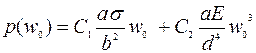, где: С₁=3,4, а С₂ – константа, зависящая от коэффициента Пуассон материала мембраны (изменяется от 2 до 3,4 при изменении коэффициента Пуассона от 0 до 0,5); σ – напряжение в мембране, Е – модуль упругости материала. При известном w₀ прогиб мембраны в любой точке с координатами х и y может быть рассчитана по уравнению: ,причем 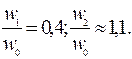Для точных расчетов поведения мембран при статических воздействиях обычно используют численное моделирование, в частности, метод конечных разностей.

На состояние и поведение упругих механических элементов в наномасштабе большое влияние может оказывать действие статических объемных и поверхностных сил, возникающих при формировании таких элементов, а также при адсорбции и/или сорбции веществ окружающей среды и проявлении других эффектов (Рис.24).

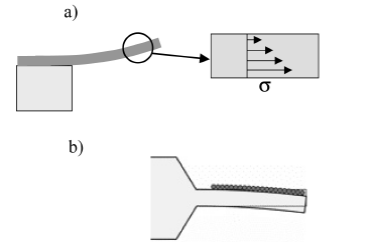
Рис.24. Схематическое изображение изгиба консольной балки с неравномерным распределением механического напряжения по толщине (а) и сжимающим слоем на верхней поверхности (б).

Объемные (внутренние, или остаточные) напряжения в наноразмерных упругих элементах, возникающие при их формировании в виде градиента напряжения Δσ по толщине и достигающие значений порядка нескольких МПа/мкм, вызывают самопроизвольный прогиб таких элементов - отклонение их нейтральной оси от ее равновесного положения в ненапряженном состоянии. Максимальное значение такого отклонения для консольной балки оценивается по формуле: .

К поверхностным силам относится разность растягивающего σ_s⁺ и сжимающего σ_s^- поверхностного натяжения на верхней и нижней поверхностях упругих элементов Δσ_s, имеющей размерность Н/м. В случае свободной тонкой пластины произвольной формы действие Δσ_s вызывает ее равномерный изгиб, радиус кривизны которого с вогнутостью со стороны действия сжимающей силы равен: 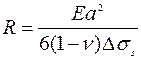, что эквивалентно действию на свободные края пластины изгибающего момента на единицу длины величиной 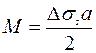. При этом прогиб напряженной пластины от исходного ненапряженного состояния как функция координат в плоскости x,у равен: 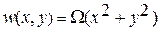, где 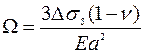- однородная постоянная кривизна пластины, равная 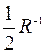[39]. Для консольной балки прямоугольного сечения эти соотношения применимы при l/b>>1 и координате y, удаленной от боковых краев балки y=в/2, т.е. близкой к 0. В этом случае при х=l и у =0 отклонение конца балки при воздействии разности поверхностного натяжения Δσ_s равно: 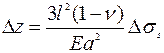[39-40].

3.1.1. Динамическое поведение упругих механических элементов

Большинство разрабатываемых МЭМП и НЭМП работают как резонаторы, в упругих механических, обычно балочных, элементах которых возбуждаются колебания основной изгибной моды. Физической основой действия таких элементов в динамических условиях является смещение (сдвиг по фазе или по амплитуде) фундаментальной (резонансной, или характерной) частоты при каком-либо воздействии на них или изменении массы. Как показано ниже, резонансная частота механических чувствительных элементов масштабируется как 1/L, и при переходе на наномасштаб ее величина и чувствительность к различным воздействиям должна резко возрастать.

Для описания динамического поведения механических резонаторов используются различные подходы. В наиболее простом из них механический резонатор рассматривается как одномерный линейный гармонический, слабо демпфирующий осциллятор. Он представляет собой некоторую эффективную массу m_эфф, связанную с упругой пружиной с эффективной жесткостью k_эфф, способную совершать свободные затухающие или вынужденные гармонические колебания с частичным рассеиванием (диссипацией) упругой энергии за счет внешнего или внутреннего трения с эффективным коэффициентом ς_эфф. Кинетика свободных колебаний, приводящих к возврату одномерного линейного гармонического демпфирующего осциллятора в равновесное состояние после вывода его из равновесия (задания некоторого начального смещения z(0), описывается дифференциальным уравнением второго порядка: 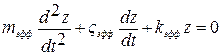. Решение этого уравнения в терминах комплексных чисел при малом ς_эфф описывает затухающие гармонические колебаний осциллятора с собственной (фундаментальной) круговой частотой ω₀=2πf₀ (радиан/с), где f₀ – периодическая частота (Гц): 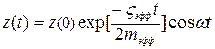. Уменьшение амплитуды этих колебаний подчиняется экспоненциальному закону: 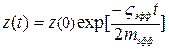, причем коэффициент 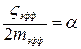называется коэффициентом затухания, а собственная частота связана с m_эфф и k_эфф соотношением: 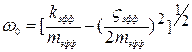. При ς_эфф →0 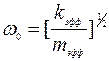или 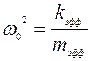. При этом . Натуральный логарифм отношения двух соседних амплитуд соответствует логарифмическому декременту затухания Δ, который связан с α соотношением: .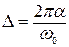

При приложении к такому осциллятору внешней силы, изменяющейся по периодическому закону с круговой частотой ω: 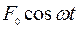, его гармонические колебаний описываются уравнением: 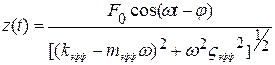, где φ – угол сдвига фаз между силой и смещением: 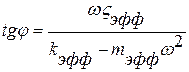. Показателем демпфирующей способности осциллятора при этом является тангенс угла потерь tgδ, где 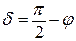, связанный с показателями затухания свободных колебаний известными соотношениями: 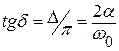. При равенстве частоты приложения внешней силы частоте собственных (свободных) колебаний (ω=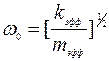) наблюдается резкое возрастание амплитуды (резонанс) до величины, равной: .

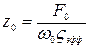Для колеблющихся консольных балок и мостиковых структур соотношения, полученные для одномерного линейного гармонического демпфирующего осциллятора, применимы вблизи резонансной частоты при правильной оценке их эффективной массы и жесткости с учетом соответствующей моды колебаний. Так как такие балки при приложении в трансверсальном направлении гармонической нагрузки ведут себя аналогично натянутой струне, то формы, которые может принимать струна или балка при колебаниях в условиях резонанса, т.е. моды их колебаний, аналитически могут быть описаны волновым уравнением: 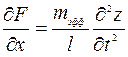. Это уравнение описывает кривизну балки как функцию времени, и его решение в координатах z-х имеет вид: 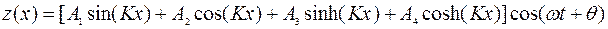где; А_n – константы, определяемые граничными условиями, 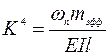. Это решение показывает, что балки при резонансе осциллируют по синусоиде вдоль оси х, а их форма определяется граничными условиями. При этом первая и основная мода колебаний балки соответствует форме, которую она принимает при статическом изгибе (при нулевой частоте и амплитудном значении прикладываемой нагрузки).

Для консольной балки 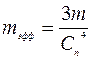, где С_n – константа, равная для первой моды (n =1) колебаний 1, 875, для второй (n =2) 4,694 и т.д. Следовательно, при ее прямоугольном сечении ав и длине l при первой моде колебаний m_эфф ≈0,23m. Для аналогичной мостиковой структуры m_эфф ≈0,735m. В этих соотношениях m – истинная масса балки, равная ablρ (abl – объем балки, ρ – плотность материала). Эффективная жесткость колеблющихся балок равна их коэффициентам упругости, рассчитываемым при статическом изгибе. 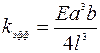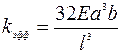Для консольной и закрепленной балок эффективная жесткость равна: и соответственно. С учетом m_эфф и k_эфф этих балок их резонансная круговая частота может быть с достаточно высокой точностью рассчитана по соотношению: 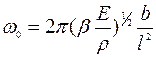, где β - коэффициент, близкий к 1. Резонансная периодическая частота заданной моды колебаний рассчитывается по соотношению: 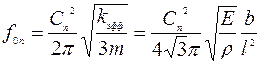[17]. Из этих соотношений следует, что резонансная частота механических чувствительных элементов масштабируется как 1/L и при переходе на наномасштаб ее величина достигает очень больших значений. Так, мостиковая структура из кремния шириной 50 нм, толщиной 80 нм и длиной 780 нм при m_эфф = 5,3х10^{-15 г и} k_эфф =290 Н/м имеет ω₀ порядка 1ГГц, а консольная балка прямоугольного сечения из поликристаллического кремния длиной 10 нм и толщиной 1 нм имеет расчетную резонансную частоту первой моды колебаний порядка 20-30 ГГц при амплитуде в резонансе 10^-3 – 10^-6 нм.

Вблизи резонансного пика частотная зависимость амплитуды вынужденных колебаний балок как одномерных линейных гармонических демпфирующих осцилляторов при отсутствии внешнего трения (вязкости среды, т.е. в вакууме, описывается соотношением 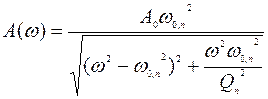, где А₀ – амплитуда колебаний при нулевой частоте; ω и ω_0,n – фактическая и резонансная (для моды n при отсутствии диссипации энергии) круговая частота соответственно; Q _n – добротность осциллятора (Q -фактор) для моды n. Величина Q является, наряду с собственной или резонансной частотой, важнейшим параметром осциллятора, равным отношению запасенной упругой энергии за один цикл колебаний (Е_з) к рассеиваемой энергии (Е_р) или к средним за цикл потерям мощности (Р/ω): 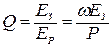. При этом запасенная энергия в механическом осцилляторе равна половине произведения амплитудных значений силы и деформации, а рассеиваемая в виде тепла в единице объема: . Величина Q- фактораопределяет избирательную и разрешающую способность осциллятора: чем больше Q, тем выше резонансный отклик системы по сравнению с нерезонансным и тем большее различие по величине откликов на одинаковые по амплитуде воздействия с близкими частотами.

При вынужденных колебаниях осциллятора Q- факторэкспериментально определяется по отношению резонансной частоты ω ₀ к ширине резонансного пика по частоте на уровне убывания его высоты в √2 раза (Δω): 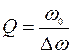(Рис.25).

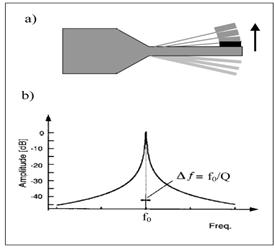
Рис.25. Схематическое изображение вибрирующей консольной балки (а) и амплитуды колебаний как функция частоты.

Величина Q зависит от механизма и интенсивности рассеяния энергии в процессе колебаний и связана с основными коэффициентами уравнения движения осциллятора и параметрами механических потерь простыми соотношениям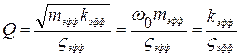и: и 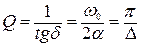. При проявлении нескольких источников диссипации энергии в колебательной системе складываются обратные величины Q -фактора: . При этом в случае многомодовых колебаний каждая из мод обладает собственным Q -фактором.

При анализе внутренних диссипативных потерь с использованием классической трехэлементной модели вязко-упругого тела (модели Зинера), состоящей из модели Максвелла (последовательного, соединения пружины и демпфера), параллельно соединенной со второй пружиной, Q -фактор обратно пропорционален тангенсу угла потерь (tgδ) материала балки и является функцией частоты: 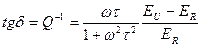, где τ – среднее время релаксации, равное отношению коэффициента вязкости демпфера к коэффициентам упругости пружин; E_u, E_r - нерелаксированный и релаксированный модуль упругости материала балки соответственно.

Q -фактор колебательных систем на основе жестких материалов обычно очень большой из-за высоких частот и малых времен релаксации и зависит преимущественно от геометрии балок и окружающей среды. Так, экспериментальные исследования зависимости Q -фактора консольных балок из поликристаллического кремния от их длины и от резонансной частоты, варьируемых в пределах от 150 мкм до 75 мкм и от 145кГц до 560 кГц соответственно, при постоянной ширине (15 мкм) и толщине (2 мкм) показали, что при малом атмосферном давлении (0,2Па) величина Q - фактора для самой длинной балки с самой низкой резонансной частотой составляла величину больше 38 000, уменьшаясь до 15 000 при уменьшении длины и возрастании резонансной частоты балки. При повышенном давлении воздуха (40Па) Q -фактор для самой длинной балки составил 6 000 и возрос до 16 000 при уменьшении длины балки до 75 мкм и возрастании резонансной частоты до 560 кГц.

Таким образом, окружающая среда с высокой плотностью ρ и вязкостью η может оказывать определяющее влияние как на резонансную частоту, так и на Q -фактор консольных балок. Теоретически влияние только плотности невязкой среды на величину ω _R,n (по сравнению с резонансной частотой в вакууме) и Q описывается следующими соотношениям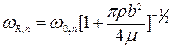и:

и 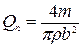, где: m=ρ_бва – масса балки на единицу длины, ρ_б – плотность материала балки.

Влияние вязкости среды на величину ω _R,n и Q -фактора свободной консольной балки при вынужденных колебаниях учитывается при этом через гидродинамическую функцию Γ (ω), определяющую изменение Q в вязкой среде по сравнению с вакуумом. Важнейшим масштабным фактором при этом является ширина балки, которая значительно меньше ее длины. Функцию Γ (ω) удалось определить только для консольной балки круглого сечения [76]: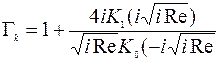, где К₀ и К₁ – модифицированные Бесселевы функции 3-го типа, Re – число Рейнольдса: 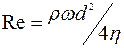, где ρ и η – плотность и вязкость среды соответственно, d – диаметр балки. Для тонкой консольной балки прямоугольного поперечного сечения, ширина которой в значительно больше толщины а, вводится поправочный коэффициент по отношению к цилиндрической балке Ω (ω), который представляет собой комплексную рациональную функцию lgRe: Ω (ω) = Ω _r(ω)+i Ω _i(ω), удовлетворяющую предельным условиям: Ω (ω)→ 1 при Re→ 0 и Re→∞ и рассчитываемую численным нелинейным методом наименьших квадратов. Соответственно, Γ_п (ω)= Ω (ω) Γ _к = Γ _r(ω)+i Γ _i(ω) ]. Значения ω_R,n и Q _n определяются при этом по соотношениям: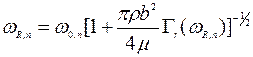и 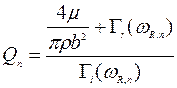соответственно.

Балочные упругие элементы часто расположены на достаточно близком расстоянии h₀ от подложки и работают в воздушной среде. Поэтому важную роль в их высокочастотных колебаниях играет так называемое демпфирование за счет выдавливания (перетекания) воздуха из промежутка между балкой и подложкой (sqeeze damping). Эффективный коэффициент демпфирования ς_эфф при первой моде колебаний, малом безразмерном параметре 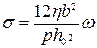и частоте, значительно меньшей критической 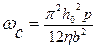, рассчитывается по соотношению: , где: η – вязкость среды, р – номинальное давление.