Раскрыв скобки в уравнении (2.3) и обозначив число  через С, приведем уравнение (2.3) к виду
через С, приведем уравнение (2.3) к виду
 . (2.4)
. (2.4)
Таким образом, каждую прямую на плоскости можно описать уравнением первой степени с переменными х и у. При этом хотя бы один из коэффициентов А или В отличен от нуля (т.к. А и В – координаты нормального вектора прямой).
Докажем обратное утверждение: если дано уравнение вида (2.4), где хотя бы один из коэффициентов А или В отличен от нуля, то линия, определяемая этим уравнением, – прямая.
Пусть В¹0. Тогда уравнение (2.4) можно записать в виде
 .
.
Как было получено выше, это уравнение определяет прямую, проходящую через точку М0 с координатами  и перпендикулярную вектору n с координатами (А, В). Если В=0, то А¹0, и рассуждения аналогичны.
и перпендикулярную вектору n с координатами (А, В). Если В=0, то А¹0, и рассуждения аналогичны.
Таким образом, доказана следующая теорема.
Теорема 2.1. В декартовой прямоугольной системе координат на плоскости:
1) каждая прямая задается уравнением первой степени  , где хотя бы один из коэффициентов А или В отличен от нуля;
, где хотя бы один из коэффициентов А или В отличен от нуля;
2) каждое уравнение вида  , где хотя бы один из коэффициентов А или В отличен от нуля, определяет прямую линию.
, где хотя бы один из коэффициентов А или В отличен от нуля, определяет прямую линию.
Уравнение  при условии, что хотя бы один из коэффициентов А или В отличен от нуля, называется общим уравнением прямой на плоскости. При этом важно помнить, что коэффициенты А и В в уравнении являются координатами нормального вектора этой прямой.
при условии, что хотя бы один из коэффициентов А или В отличен от нуля, называется общим уравнением прямой на плоскости. При этом важно помнить, что коэффициенты А и В в уравнении являются координатами нормального вектора этой прямой.
Запишем уравнение прямой  , проходящей через точку М0(х0,у0) параллельно ненулевому вектору a = (p,q).
, проходящей через точку М0(х0,у0) параллельно ненулевому вектору a = (p,q).
Любой ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Вектор a = (p,q),  , – направляющий вектор прямой
, – направляющий вектор прямой  .
.
Возможны следующие случаи:
1) p = 0, q ¹ 0. Тогда вектор a параллелен оси Оу: a = 0× i + q × j = q × j, значит прямая 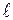 параллельна оси Оу и уравнение прямой
параллельна оси Оу и уравнение прямой 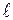 имеет вид
имеет вид  (см. пример 2 на стр.37).
(см. пример 2 на стр.37).
2) q = 0, p ¹ 0. Тогда вектор a параллелен оси Ох: a = p × i + 0× j = p × i значит прямая  параллельна оси Оx и уравнение прямой
параллельна оси Оx и уравнение прямой  имеет вид
имеет вид 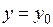 (см. пример 2 на стр.37).
(см. пример 2 на стр.37).
3) p ¹ 0, q ¹ 0. Точка М(х,у) принадлежит прямой  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  и a коллинеарны, а значит тогда и только тогда, когда существует k (k¹0):
и a коллинеарны, а значит тогда и только тогда, когда существует k (k¹0):  = k a, или
= k a, или
 . (2.5)
. (2.5)
Уравнение (2.5) является уравнением прямой, проходящей через точку М0(х 0, у 0) параллельно вектору a = (p, q) (p ¹ 0, q ¹ 0). Для каждой прямой существует бесчисленное множество направляющих векторов, причем все они коллинеарны друг другу (докажите самостоятельно).
Запишем уравнение прямой  , проходящей через две данные точки М1(х 1, у 1) и М2(х 2, у 2). Пусть сначала
, проходящей через две данные точки М1(х 1, у 1) и М2(х 2, у 2). Пусть сначала  и
и  . В этом случае за направляющий вектор прямой
. В этом случае за направляющий вектор прямой  можно принять вектор
можно принять вектор 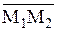 , координаты которого равны соответственно
, координаты которого равны соответственно 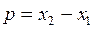 и
и  . Подставив в (2.5) координаты направляющего вектора получим уравнение прямой, проходящей через точку М1(х 1, у 1) параллельно вектору
. Подставив в (2.5) координаты направляющего вектора получим уравнение прямой, проходящей через точку М1(х 1, у 1) параллельно вектору 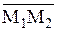
 . (2.6)
. (2.6)
Итак, уравнение (2.6) – уравнение прямой, проходящей через две данные точки М1(х 1, у 1) и М2(х 2, у 2), где  и
и 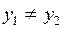 . В случае
. В случае 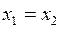 прямая параллельна оси Оу и ее уравнение имеет вид
прямая параллельна оси Оу и ее уравнение имеет вид  ; в случае
; в случае 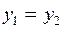 прямая параллельна оси Ох и ее уравнение:
прямая параллельна оси Ох и ее уравнение: 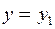 .
.
Пример. Написать уравнение средней линии треугольника АВС, параллельной стороне АВ, если А(1,3), В(–1,1), С(3,–5).
○ Пусть точка М – середина стороны АС. Тогда прямая, содержащая среднюю линию треугольника АВС, параллельную стороне АВ, это прямая 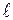 , проходящая через точку М параллельно прямой, содержащей сторону АВ. Значит, вектор
, проходящая через точку М параллельно прямой, содержащей сторону АВ. Значит, вектор 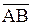 можем взять в качестве направляющего вектора прямой
можем взять в качестве направляющего вектора прямой 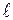 . Найдем координаты вектора
. Найдем координаты вектора 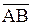 :
: 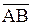
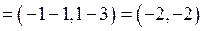 . Найдем координаты точки М. Так как точка М– середина стороны АС, то 2
. Найдем координаты точки М. Так как точка М– середина стороны АС, то 2 =
=  , или
, или

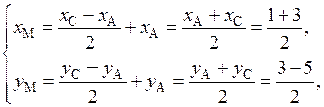
Откуда имеем  . Теперь, воспользовавшись уравнением (2.5), можем написать искомое уравнение:
. Теперь, воспользовавшись уравнением (2.5), можем написать искомое уравнение: 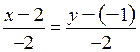 , или
, или 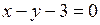 . ●
. ●
 2014-02-12
2014-02-12 823
823








