Криволинейные ортогональные координаты

ЛЕКЦИЯ 10

Лист регистрации изменений

Задание для самостоятельной работы

Изучить:

1. Влияние ФП на служебно-профессиональную деятельность сотрудника ГПС МЧС.

2. Специальная направленность ФП.

3. Разделы ФП в НФП ГПС МЧС, их общая характеристика.

4. Оценка индивидуальной физической подготовленности сотрудника ГПС МЧС.

5. Общие и специальные задачи ФП сотрудников ГПС.

Вопросы для самоконтроля:

1. Содержание физической подготовки.

2. Основное средство физической подготовки.

3. Формы физической подготовки.

Номер измене­ния	Номера листов	Основание для внесения изменений	Подпись	Расшифровка подписи	Дата	Дата введения изменения
заменен­ных	новых	аннулиро­ванных

Криволинейные ортогональные координаты. Коэффициенты Ламе. Дифференциальные операции в ортогональной системе координат. Цилиндрическая и сферическая системы координат. Центральные, осевые и осесимметричные скалярные поля.

9*. ПРИМЕНЕНИЕ КРИВОЛИНЕЙНЫХ КООРДИНАТ В
ВЕКТОРНОМ АНАЛИЗЕ

Такие величины, как градиент, дивергенция, ротор и другие, часто встречаются в различных задачах теоретической и математической физики. Во многих случаях полезно уметь записывать эти величины не только в декартовых, но и в тех или иных криволинейных системах координат. Например, если рассматриваемое поле обладает сферической симметрией, т.е. в каждой точке рассматриваемая величина зависит только от расстояния этой точки до начала координат, то, ясно. Что все формулы, связанные с данным полем, должны значительно упроститься в сферической системе координат.

Говорят, что в пространстве задана система координат, если каждой точке P поставлено в соответствие ройка чисел { q ₁, q ₂, q ₃}, причем различным тройкам чисел отвечают различные точки пространства. Числа q ₁, q ₂, q ₃ называются координатами точки P=P (q ₁, q ₂, q ₃).

Линией, вдоль которой изменяется только одна координата q_i, а остальные фиксированы, называется координатной q_i - линией. Поскольку, в общем случае, координатные q ₁, q ₂ и q ₃ линии отличны от прямых линий, то поэтому координаты { q ₁, q ₂, q ₃} называются криволинейными. Если координатные линии являются прямыми, то такие координаты называются декартовыми.

Пусть декартовы и криволинейные координаты связаны формулами:

x = x (q ₁, q ₂, q ₃), y = y (q ₁, q ₂, q ₃), z = z (q ₁, q ₂, q ₃). (9.1)

Поскольку через каждую точку P пространства проходит три координатных линии q ₁, q ₂, q ₃, то в этой точке можно построить базис { r ₁, r ₂, r ₃}, естественным образом связанный с координатными линиями, т.е. так, чтобы каждый вектор r_i был касательным к соответствующей координатной линии и направлен в сторону возрастания координаты q_i. Для этого вычислим производные 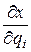, , 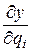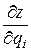в точке P. Очевидно, что эти производные будут представлять собой координаты вектора касательной к q_i -линии, т.е. можно принять

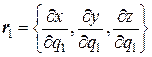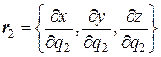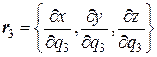, , . (9.2)

Для того чтобы векторы r ₁, r ₂, r ₃ образовывали базис, необходимо и достаточно, чтобы они были неколлинеарными, т.е. чтобы определитель

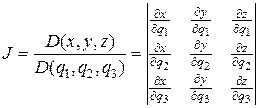(9.3)

был отличен от нуля. Другими словами, якобиан перехода от криволинейных координат к декартовым должен быть отличен от нуля: J¹0.

Введем в точке P нормированный базис, состоящий из трех единичных векторов: e ₁, e ₂ и e ₃, касательных к координатным линиям, проходящих через точку M:

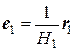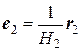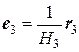, , , (9.4)

где

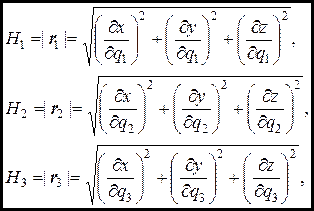(9.5)

называются коэффициентами Ламе.

Заметим, что в отличие от декартовой системы координат, определяемой тремя единичными векторами, в криволинейной системе координат базис { e ₁, e ₂, e ₃} будет меняться от точки к точке, т.е. сами векторы e ₁, e ₂, e ₃ представляют собой функции параметров q ₁, q ₂, q ₃. Однако это не мешает любой вектор, заданный в произвольной точке M (т.е. любое векторное поле), в виде линейной комбинации векторов e ₁, e ₂, e ₃.

В дальнейшем мы ограничимся простейшим и в то же время наиболее важным случаем ортогональных координат. система криволинейных координат называется ортогональной, если в любой точке три координатные линии, проходящие через эту точку, ортогональны друг другу. Другими словами, в каждой точке базис r ₁, r ₂, r ₃ является ортогональным (а базис e ₁, e ₂, e ₃ – ортонормированным). Отметим, что свойством ортогональности обладают, в частности, цилиндрические и сферические координаты.

9.2. Дифференциальные операции в ортогональной
системе координат