Проверка статистических гипотез о параметрах

законов распределения случайных величин.

Пример №1:

Проверка гипотезы о математическом ожидании нормально распределенной случайной величины X.

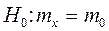
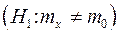
Если дисперсия Dx известна, то в качестве меры рассогласования U берем статистику

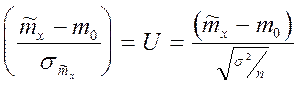где ,

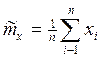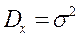
Величина U подчинена нормированному нормальному закону распределения с

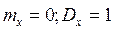. В качестве критической принимается двухсторонняя симметрич- ная область .

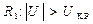Величина Uкр ищется из условия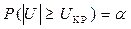

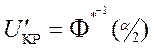¦(u)

a/2

a/2

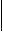
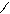
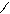
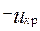
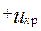U

Если дисперсия Dx - неизвестна, то

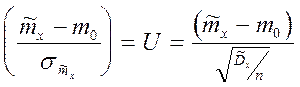, где

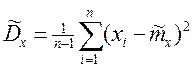
Величина U распределена по закону распределения Стьюдента с (n-1) степенью свободы. Критическая область имеет тот же вид, но значения 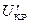и 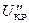берутся из t-распределения с (n-1) степенью свободы.

Если | U | < Uкр, то гипотеза Ho - принимается.

Пример №2:

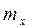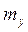Проверка гипотезы о равенстве средних значений и двух независимых нормально распределенных случайных величин X и Y.

1. Дисперсии Dx и Dy - известны.

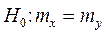
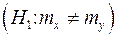
В качестве меры рассогласования используется величина

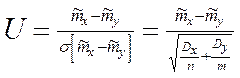(n, m - объемы выборок случ. величин X и Y)

U - распределена по нормированному нормальному закону распределения.

Если | U | < Uкр, то гипотеза принимается.

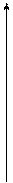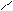
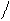
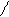
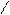
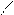
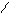
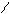
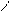
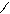
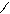
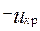
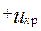¦(u)

U

2. Дисперсии Dx и Dy - неизвестны.

Если n и m - велики (> 30), то можно использовать то же U, но вместо Dx и Dy использовать их оценки. Закон распределения U близок к нормальному.

Если n и m - малы и Dx = Dy = D, то

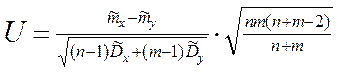
т.к.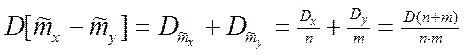

В качестве оценки D целесообразно использовать все (n+m) наблюдений.

Отсюда (т.к. mx = my):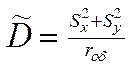

где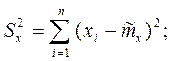

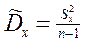
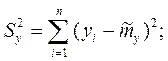
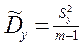
rоб = n+m-2 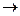общее число степеней свободы.

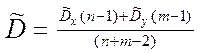, отсюда

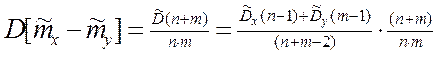
U - подчинена t-распределению Стьюдента с r = n+m-2.

Критическая область - двухсторонняя.

(можно использовать, есл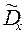и и 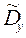различаются незначимо)

Пример №3:

Проверка гипотезы о значении дисперсии нормально распределенной случайной величины Х при неизвестном среднем (математическом ожидании).

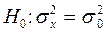
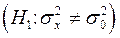
В качестве меры U используем статистику

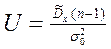подставим 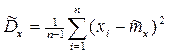; получим, что:

величина U подчинена 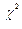-распределению с (n-1) числом степеней свободы. В качестве критической выбирается квазисимметричная двухсторонняя область.

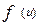
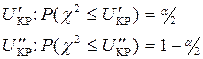
a/2 a/2

· ·

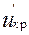
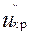u

Если вычисленное значение 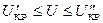, то гипотеза Ho - принимается.

Пример №4:

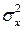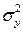Проверка гипотез о равенстве дисперсий и двух независимых нормально распределенных случайных величин X и Y при неизвестных средних 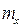и .

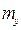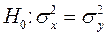
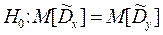
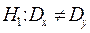
В качестве меры расхождения используем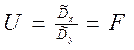

где 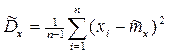, а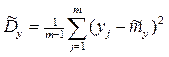

Здесь оценк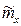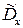и , и 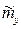, 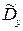получены в результате наблюдений над случайными величинами X и Y по выборкам объема n и m соответственно.

Величина U подчинена F-распределению с числом степеней свободы (n-1) - в числителе и (m-1) - в знаменателе. Критическая область - квазисимметричная двухсторонняя, границы которо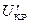й и 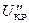ищутся из F-распределения при заданном уровне значимости.

· ·

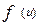
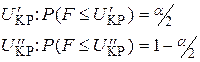
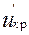
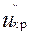u

т.к. для F-распределения 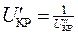, а в таблице обычно дается одно значение Fкр при условии P(F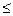Fкр) = 0.95, 0.99,..., т.е. фактически 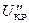, то 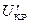ищется из 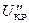. При вычислении значения F = U в числителе всегда ставится большая из оценок 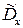или .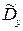

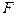
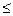
Можно показать, что если вычисленное таким образом значение 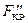, найденного из таблицы F-распределения при соответствующих числах степеней свободы и уровне значимости 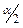, то при этом выполняется и условие 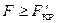, таким образом, гипотеза о равенстве дисперсий принимается (т.е. различие дисперсий несущественно - незначимо).