Свойства вероятностей (следствия из аксиом)

1. Вероятность невозможного события равна нулю: Р(Æ)=0

Доказательство: Так как невозможное событие Æ несовместно с любым другим событием А, АÆ=Æ, то из аксиомы 3 следует, что Р(АÈÆ)=Р(А)+Р(Æ). С другой стороны, так как АÈÆ=А (добавление невозможного события не изменяет события А), то Р(АÈÆ)=Р(А). Следовательно, Р(Æ)=0.ð

2. Р(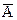)=1-Р(А)

Доказательство: Из 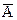А+ =W, А 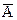=Æ и аксиом 2,3 следует:

P(A)+P(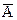)=P(W), P(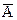)=1-P(A) —

3. Если АÌВ, то Р(А)£Р(В)

Доказательство: Разложим В на два несовместных события: В=А+ 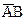. Получим в силу аксиомы 3: Р(В)=Р(А)+Р(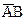), откуда следует, что Р(В)³Р(А). ž

Таким образом, если событие А может произойти только вместе с событием В, то вероятность события А не может быть больше вероятности события В.

4. Р(А)£1 для любого А.

Доказательство: Из того, что любое событие А может произойти только с достоверным событием: А=АWÌW, а также из свойства 3 и аксиомы 2 следует Р(А)£Р(W)=1.?

5. Теорема сложения вероятностей. Для любых А и В справедливо

Р(АÈВ)=Р(А)+Р(В)-Р(АВ)

Доказательство: AÈB=A+B ,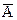

P(AÈB)=P(A)+P(B 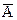) (1)

C другой стороны, любое событие можно разложить на два несовместных события:

B=A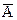B+ B,

P(B)=P(AB)+P(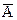 B), откуда

P(B 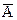)=P(B)-P(AB).

Подставляя это выражение для Р(В 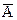) в (1) получаем:

Р(АÈВ)=Р(А)+Р(В)-Р(АВ) —

6. Теорема сложения вероятностей для n событий:

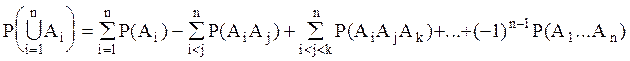
Доказательство: Методом математической индукции. При n=2 теорема доказана. Пусть она верна для (n-1) события; покажем, что при этом она верна для n событий. Обозначим В= 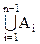, тогда

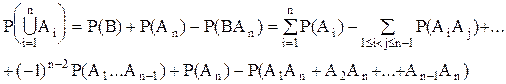(2)

В свою очередь для (n-1) событий вида 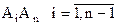имеем:

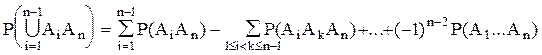(3)

Подставляем (3) в (2) и получаем утверждение теоремы. †

7. Если ВÌА, то Р(А-В)=Р(А)-Р(В)

Доказательство:

А=В+(А-В);

Р(А)=Р(В)+Р(А-В); а это влечет:

Р(А-В)=Р(А)-Р(В). ƒ

8. Аксиома непрерывности.

Функция множеств Р(А) - непрерывна. Если А_n есть монотонно возрастающая последовательность множеств: A₁ÌA₂ÌA₃...ÌA_nÌ... и 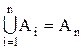, , тогда

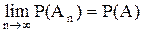
Доказательство: Согласно определению:

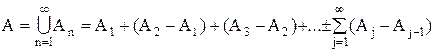
Если А₀=Æ

—

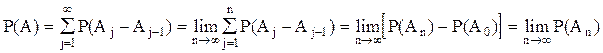Определение вероятности, как меры измеримого пространства событий, позволяет по заданным (или определенным из эксперимента) вероятностям одних событий находить вероятности других более сложных событий, используя действия над событиями и свойства вероятности. Однако, данное определение не задает конкретную величину вероятности событий. Её можно определить теоретически лишь в некоторых частных случаях, и в общем случае - оценить экспериментально. Рассмотрим частные случаи, в которых вероятности событий можно рассчитать теоретически.