декабря 1962 г

ПРЕДИСЛОВИЕ АВТОРА К НЕМЕЦКОМУ ИЗДАНИЮ

Математика — широкое поприще идей, и ее история знакомит нас с некоторыми из благороднейших помыслов неисчислимых поколений. Можно было сжать эту историю до объема книги меньше, чем в триста страниц, только подчиняясь суровому требованию — давать очерк развития немногих основных идей и сводить к минимуму описание других направлений. Биографии сведены к наброскам, многие достаточно важные авторы, например Гоберваль, Ламберт, Шварц, опущены. Но, быть может, наибольший ущерб причинен неполнотой описания общей культурной и общественной атмосферы, в которой формировалось (или затухало) развитие математики в ту или иную эпоху. На математику оказывали влияние земледелие, торговля и промышленность, военное дело, инженерное дело и философия, физика и астрономия. Влияние гидродинамики на теорию функций, влияние кантианства и землемерия на геометрию, электромагнетизма — на теорию дифференциальных уравнений, картезианства — на механику и схоластики — на математический анализ — обо всем этом можно было сказать лишь несколько фраз или, пожалуй, несколько слов. Между тем добиться понимания хода развития и содержания математики можно лишь при учете всех этих определяющих факторов. Ссылка на литературу нередко заменяет исторический анализ. И наша история заканчивается 1900-м годом, так как современная математика — настолько многосторонняя наука, что невозможно — по крайней мере для автора этой книги — дать компетентную оценку хотя бы ее основных направлений¹).

') См в связи с этим Weyl H. A. Halfcentury of Malhematics / Amer. Math. Monthly.—1951.—V. 58.—P. 523—553.

Все же я надеюсь, что, несмотря на такие ограничения удалось дать вполне добросовестное описание главных направлений, по которым в течение веков шло развитие математики, и тех общественных и культурных условий, в которых оно происходило. Конечно, отбор материала не был обусловлен только объективными факторами — сказывались симпатии и антипатии автора, степень его осведомленности.

Что касается последнего, надо сказать, что не всегда автор мог непосредственно опираться на источники, слишком часто приходилось пользоваться источниками из вторых и даже третьих рук. Поэтому следует посоветовать (что относится не только к этой книге, но и ко всем исследованиям такого рода) по возможности проверять утверждения автора, обращаясь к оригиналам. По многим причинам это является правильным положением. При изучении таких авторов, как Евклид, Диофант, Декарт, Лаплас, Гаусс или Риман, не следует ограничиваться только цитатами из исторических книг, в которых описаны их труды. В подлинниках Евклида и Гаусса содержится такая же живительная сила, как и в подлинниках Шекспира; у Архимеда, у Ферма, у Якоби можно найти столь же великолепные места, как у Горация или Эмерсона ').

В число положений, которыми руководствовался автор при изложении материала, входили следующие четыре:

1. Подчеркивать связи и родство восточных цивилизаций, а не исходить из механического разбиения на египетскую, вавилонскую, китайскую, индийскую и арабскую культуры.

2. Проводить различие между установленными фактами, гипотезами и преданиями, особенно в греческой математике.

3. Связать два течения в математике Возрождения, арифметикоалгебраическое и «флюкционное», с торговыми и техническими запросами эпохи соответственно.

4. Строить изложение математики девятнадцатого столетия больше по лицам и школам, чем по предметам. (Здесь в качестве основного руководства можно было принять книгу Клейна «Лекции о развитии математики в XIX столетии».) Изложение по отдельным дисциплинам дают книги Кеджори и Белла, а с большим числом тех

¹) Эмерсон Ралф Уолдо (1803—1882) — известный американский критик, поэт и моралист.

нических подробностей — немецкая «Энциклопедия математических наук» (Enzyklopadie der mathematischen Wissenschaften, 24 тома, Лейпциг, 1898—1935) и Repertorium der hoheren Analysis (5 томов, Лейпциг, 1910—1929) Паскаля (Pascal).

Автор выражает свою благодарность О. Нейгебауеру, который охотно согласился прочесть первые главы книги, что дало возможность во многих местах улучшить изложение. Профессору А. П. Юшкевичу автор обязан многими улучшениями при изложении науки стран ислама.

Во втором английском издании исправлены многие опечатки и ошибки, имевшиеся в первом издании. Автор благодарен Р. Арчибалду (R. С. Archibald), Э. Дейкстерхойсу (Е. J. Dijksterhuis), С. Иоффе (S. A. Joffe) и другим читателям книги, благодаря вниманию которых эти погрешности были обнаружены. В немецкое издание были внесены новые исправления.

Д. Стройк

ВВОДНЫЙ ОБЗОР ЛИТЕРАТУРЫ

Ниже приводится список ряда важнейших книг по истории, математики в целом. В этом списке не нуждаются те читатели, которые могут воспользоваться книгой Sarton G. The Study of the History of Mathematics.— Cambridge, 1936, содержащей не только интересное введение в наш предмет, по и полную библиографию. Данные о более поздней литературе можно найти в соответствующих отделах реферативных журналов по математике: Jahrbuch iiber die Fortschritte der gesamten Malhematik (нем.), Mathematical Reviews (амер.), Zentralblatt ftir Mathemalik (нем.) и реферативный журнал «Математика» (изд. Института научной информации АН СССР, с 1953 г.).

Работы советских ученых по истории математики приведены в библиографических указателях: История естествознания. Литература, опубликованная в СССР (1917—1947).— М., 1949; История естествознания. Литература, опубликованная в СССР (1948— 1958).— М., 1955. Полезна также книга Библиографические источники по математике и механике, изданные в СССР за 1917—1952 гг.—М.; Л., 1957. Кроме того, см. Зубов В.П. Историография естественных наук в России.— М., 1956.

Книги на английском языке:

Archibald R. С. Outline of the History of Mathematics.— 6th ed.— Amer. Math. Montrly.— Jan. 1949.— № 561.

Эта книга в 114 с. дает прекрасный очерк истории математики и содержит много библиографических указаний.

Cajori F. A. History of Mathematics.—2nd ed.— N. Y., 1938. Это образцовая книга в 514 с.

Smith D. Е. History of Mathematics. V. I.— Boston, 1923. V. II. Boston, 1925.

Автор книги ограничился в основном изложением истории элементарной математики, но приводит данные о всех выдающихся математиках и многочисленные иллюстрации, новые издания— 1951 — 1953, 1958.

Bell E. Т. Men of Mathematics.—N. Y., 1937.

Bell E. T. The Development of Mathematics.—2nd ed.—N. Y.; London, 1945.

Эти две книги содержат обширный материал как о математиках, так и об их достижениях. Вторая книга посвящена главным образом математике XIX—XX вв.

Scott J. F. A History of Mathematics from Antiquity to the Beginning of the Nineteenth Century.— London, 1958.

Тurnbull H. W. The Great Mathematicians.— London. 1929. Новое изд. N. Y., 1961.

Преимущественно элементарная математика рассматривается в книгах:

Sanford V. A. Short History of Mathematics.— Boston, 1930.

Rouse Ball W. VV. A Short Account of the History of Mathematics.— 6th ed.— London, 1915; переиздана в 1960 г.

Хорошо написанная, но устаревшая книга.

Eves H. An Introduction to the History of Mathematics.N. Y., 1953.

Интересный материал собран в книге Сajогi F.A. History of Mathematical Notations. V. I.— Chicago, 1928. V. II. Chicago, 1929.

Образцовой книгой по истории математики все еще остается

Cantor M. Vorlesungen fiber Geschichte der Mathematik.— Bd 1—4.— Leipzig, 1900–1908.

Эта работа большого масштаба (четвертый том написан группой специалистов под общим руководством М. Кантора) охватывает историю математики до 1799 г. Во многих местах она устарела, особенно в разделах об античной математике, во многих частностях она ошибочна, но, как и раньше, она хороша для первой ориентировки.

Поправки к ней Эиестрема (G. Enestrom) и др. публиковались в журнале Bibliotheca Mathematica.

Другие книги на немецком языке:

Zeuthen H. G. Geschichle der Mathematik im Alterlum und Mittelalter.— Kopenhagen, 1896 (французское издание — Paris, 1902; первое датское издание вышло в

1893 г., в 1949 г. появилось второе датское издание, переработанное О. Нейгебауером, русский перевод (с нем. издания): Цейтен Г. Г. История математики в древности и в средние века.— 2е изд.— М.; Л.: ГОНТИ, 1938).

Zeuthen H. G. Geschichte der Mathematik im 16 und 17. Jahrhundert.—Leipzig, 1903; русский перевод: Цейт.ен Г. Г. История математики в XVI и XVII столетиях. 2-е изд. М.; Л.: ГОНТИ, 1938.

Giinther S., Wieleitner H. Geschichte der Mathematik.— Bd 1—2 (первый том написан Гюнтером, издано Вилейтнером).— Berlin, 1939. Написанная Вилейтнером часть вошла в русское издание: Вилейтнер Г. История математики от Декарта до середины XIX столетия.— М.: Физматгиз, 1960. 2е изд.— М.: Наука, 1966.

Tropfke J. Geschichte der Elmentarmathematik.— 2 Aufl. Bd 1–7. Leipzig, 1921-1924. 3 Aufl.— Bd 1 — 4. Leipzig, 1930-1940.

Первая часть первого тома переведена на русский язык: Тропфке И. Арифметика.— М., 1914.

В издание: Die Kultur der Gegenwart III, I.— Leipzig; Berlin, 1912 вошли работы:

Zeuthen H. G. Die Mathematik im Altertum und im Mittelalter; Voss A. Die Beziehungen der Mathematik zur allgemeinen Kultur; Timerding H. E. Verbreitung mathematischen Wissens und mathematischer Auffassung.

Becker O., Hofmann J. E. Geschichte der Mathematik.— Bonn, 1951.

Hofmann J. E. Geschichte der Mathematik.— Bd 1— 3.— Собрание Goschen.— Bd 226, 875, 882, Berlin, 1953— 1957.

Эти книги содержат подробный указатель литературы.

Becker О. Grundlagen der Mathematik in geschichtlicher Entwicklung.— Freiburg; Miinchen, 1954.

Немецкий перевод книги А. П. Юшкевича (см. ниже) является ее вторым, улучшенным изданием.

Старейшая книга по истории математики на французском языке

Montucla J. E. Historie des mathematiques.— T. 1— 4.— Paris, 1799—1802. Первое издание, в двух томах, появилось в 1758 г. Труд, где рассматривается прикладная математика, и сейчас представляет интерес.

Весьма интересна книга, выпущенная под коллективным псевдонимом группы современных математиков,

Bourbaki, Nicolas. Elements d'histoire des mathematiques.— Paris, 1961.

Всю историю математики охватывают соответствующие главы большого коллективного труда

Hisloire generale des Sciences.— Т. 1—3.— Paris, 1960—1964, под общей редакцией профессора Татона (R. Taton).

Укажем также:

D'Oсagne M. Histoire abregee des Sciences mathematiques/Ouvrage recueilli et acheve par R. Dugas.— Paris, 1952.

Книга дает краткие очерки об ученых. Dedron I., Itard J. Mathematiques et mathematiciens.— Paris, 1919.

На итальянском языке есть хорошая книга: Loria G. Storia delle mathematiche.— T. 1—3.— Torino, 1929—1933. См. также Bortolotti E. Storia della matematica elementare.— T. 3.— Milano, 1950.— P. 2.. Кроме того, укажем:

Caruccio E. Mathematica e logica nella storia e nel pensiero contemporaneo.— Torino, 1958.

Книги на русском языке:

Кольман Э. Я. История математики в древности.— М.; Физматгиз, 1961.

Юшкевич А. П. История математики в средние века.— М.: Физматгиз, 1961.

Рыбников К. А. История математики.— Т. I.— М., 1960. Т. II.— М., 1963.

Шереметьевский В. П. Очерки по истории математики.— М., 1940.

Гнеденко Б. В. Очерки по истории математики в России.— М.; Л.: Гостехиздат, 1946.

Юшкевич А. П. История математики в России до 1917 г.— М.: Наука, 1968.

Б у р б а к и Н. Очррки по истории математики/Перевод с франц. И. Г. Башмаковой под ред. К. А. Рыбникова, М.: ИЛ, 1963.

История отечественной математики /Отв. ред. И. 3. Штокало. Т. I.— Киев, 1966. Т. П.— Киев, 1967. Т. III.— Киев, 1968. Т. IV (в двух книгах).— Киев, 1970. В первых двух томах изложение доведено до 1917 г., третий и четвертый тома посвящены советскому периоду. История математики с древнейших времен до начала XIX столетия/Под ред. А. П. Юшкевича, Т. I: С древнейших времен до начала нового времени.— М.: Наука,

1970. Т. II: Математика XVII столетия.— М.: Наука, 1970 Т. III: Математика XVIII столетия.— М.: Наука, 1970.

Имеются также историко-математические антологии;

Smith D. E. A Source Book iu Mathematics.—N. Y., 1929.

Wieleitner A. Mathemalische Quellenbucher.— Bd 1—4.— Berlin, 1927—1929; русский перевод; Вилейтнер Г. Хрестоматия по истории математики, составленная по первоисточникам, вып. 1—4.— М.; Л.: ГТТИ, 1932. 2е изд. М.; Л.: ОНТИ, 1935.

Speiser A. Klassische Sliicke dor Malhematik.— Zurich; Leipzig, 1925.

Newmann I. R. The World of Mathematics.— V. 1— 4. N. Y., 1956.

Это сборник очерков о математике и о математиках.

Полезна также книга:

Callandier E. Celebres problemes mathematiques.— Paris, 1949.

Имеются также книги по истории отдельных дисциплин. Мы укажем следующие работы.

Dickson L. E. History of the Theory of Numbers.— V. 13.Washington, 19191927.

Muir T. The Theory of Determinants in the Historical Order of Development.—V. 1—4.—London, 1906—1923; Contributions to the History of Determinants 1900—1920.— London, 1930.

von Braunmuhl A. Vorlesungen uber Geschichte der Trigonomentrie. Bd 1.— Leipzig, 1900. Bd 2,— Leipzig, 1903.

Dantzig T. Number, The Language of Science.— 3rd ed.—N. Y., 1943.

Coolidge J. L. A History of Geometrical Methods.— Oxford. 1940.

Loria G. II passato e il presente delle principal! teorie geometriche.— 4 ed.— Torino, 1931.

Loria G. Storia della geometria descrittiva delle origine sino ai giorni nostri.— Milano, 1921.

Loria G. Curve piani special! algebriche e transcendenti.— T. 1—2.— Milano, 1930; нем. изд., Bd 1.— Leipzig, 1910; Bd 2. Leipzig, 1911.

Cajori F. A History of Mathematical Notations. V. 1.— Chicago, 1928. V. 2.— Chicago, 1929.

Karpinski L. C. The History of Arithmetic. — Chicago, 1925.

Walker H. W. Studies in the History of Statistical Methods.— Baltimore, 1929.

Reiff R. Geschichte der unendlichen Reihen,— Tubingen, 1889.

Todhunter I. History of the Progress of the Calculus of Variations during the Nineteenth Century.— Cambridge, 1861.

Todhunter I. History of the Mathematical Theory of Probability from the Time of Pascal to that of Laplace.— Cambridge, 1865.

Todhunter I. History of the Mathematical Theory of Attraction and the Figure of Earth from the Time of Newton to that of Laplace.— London, 1873.

Coolidge J. L. The Mathematics of Great Amateurs.— Oxford, 1949.

Archibald R. C. Mathematical Tables Makers.— N. Y., 1948.

Dugas R. Histoire de la mecanigue.—Neufchatel, 1950.

Воуer C. History of Analytic Geometry.— N. Y., 1956.

Воуer C. History of the Calculus and its Conceptual Development.— N. Y., 1949, 1959.

Beth E. W. Geschiedenis der logica.— Haag, 1944.

Из книг на русском языке по истории отдельных дисциплин укажем:

Тимченко И. Ю. Основания теории аналитических функций, ч. I: Исторические сведения о развитии понятий и методов, лежащих в основании теории аналитических функций.— Одесса, 1899; также в «Записках матем. отделения Новороссийского общества естествоисп.»— Одесса, 1892. Т. 12; 1896. Т. 16; 1899. Т. 19.

В этой книге собран огромный материал по истории развития основных понятий анализа.

Каган В. Ф. Исторический очерк развития учения об основаниях геометрии.— Одесса, 1907; также в «Записках Новороссийского университета».— Одесса, 1907.— Т. 108 и 109. Каган В. Ф. Основания геометрии, ч. I.— М.; Л.: Гостехиздат, 1949.

Васильев А. В. Целое число. Исторический очерк.— Пг., 1919, 1922.

Кеджори Ф. История элементарной математики/ Перевод с англ, и дополнения И. Ю. Тимченко.— 2е изд.— Одесса, 1917.

Беллюстин В. Как постепенно дошли люди до настоящей арифметики.— М., 1940.

Маркушевич А. И,. Очерки по истории теории аналитических функций.— М.; Л.: Гостехиздат, 1951.

Деимаи И. Я. История арифметики.— М., 1959.

Медведев Ф. А. Развитие теории множесгв в XIXвеке. М., 1965.

Паплаускас А. Б. Тригонометрические ряды от Эйлера до Лебега.— М., 1966.

Песин И. Н. Развитие понятия интеграла.— М.,1966.

Майстров Л. Е. Теория вероятностей. Исторический очерк.— М., 1967.

См. также литературу в конце каждой главы.

История математики излагается и в книгах по общей истории науки. Образцовым трудом является Sarton G. Introduction to the History of Science.— V. 1—5.— Washington; Baltimore, 1927—1948.

Изложение доведено до четырнадцатого столетия. В нашей книге транскрипция греческих и восточных имен дается, в основном, по Сартону.

Дополнением к пяти томам Сартона является книга Sarton G. The Study of the History of Science, with an Introductory Bibliography.— Cambridge, 1936').

Хорошая книга для школ:

Sedgwick W. Г., Tyler H. W. A Short History of Science. 2nd ed N. Y., 1939.

Влияние математики на культуру рассматривается в книге: Kline M. Mathematics in Western Culture.— N. Y., 1953.

Полезны также десять статей Миллера (G. A. Miller): A first Lesson in the History of Mathematics, A second Lesson и т. д. в «National Mathematics Magazine», (с 1939. V. 13 до 1945. V. 19).

Периодические издания по истории математики или по истории естествознания в целом и т. п.:

Bibliotheca mathemalica, серии 1—3 (1884—1914).

Scripta mathematica (с 1932).

Isis (с 1913).

Revue d'histoire des sciences (c 1947).

Archives internationales d'histoire des sciences (c 1947).

Centaurus (c 1950).

NTM. Z. f. Geschichte der Naturwissenschaften, Technik und Medizin (c 1960).

') См. также книгу Сартона, указанную на с. 13.

Archiv fur Geschichte der Mathematik, der Naturwisscnschaflen und der Technik (1909—1931).

Physis (c 1959).

Archive for History of Exact Sciences (c 1960).

Mitteilungen zur Geschichte der Medizin, Naturwissenschaft und Technik (Referatenorgan, с 1961).

Вопросы истории естествознания и техники (с 1956),

Историко-математические исследования (с 1948).

См. также Труды Института истории естествознания АН СССР, тт. I—IV, 1947—1952, и продолжение этого издания под названием Труды Института истории естествознания и техники АН СССР, 1954—1962 (по истории физикоматематических наук, т. 1, 5, 10, 15, 17, 19, 22, 28, 34, 43).

Глава I

НАЧАЛО

1. Наши первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века — палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях, мало отличавшихся от жизни животных, и их энергия уходила преимущественно на добывание пищи простейшим способом — собиранием ее, где только это было возможно. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки. Возможно, рисунки в пещерах Франции и Испании (давности порядка 15 тысяч лет) имели ритуальное значение, но несомненно в них обнаруживается замечательное чувство формы.

Пока не произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, люди мало продвинулись в понимании числовых величин и пространственных отношений. Лишь с наступлением этого фундаментального перелома, переворота, когда пассивное отношение человека к природе сменилось активным, мы вступаем в новый каменный век, в неолит.

Это великое событие в истории человечества произошло примерно десять тысяч лет тому назад, когда ледяной покров в Европе и Азии начал таять и уступать место лесам и пустыням. Постепенно прекращались кочевые странствия в поисках пищи. Рыболовы и охотники все больше вытеснялись первобытными земледельцами. Такие земледельцы, оставаясь на одном месте, пока почва сохраняла плодородие, строили жилища, рассчитанный на более долгие сроки. Стали возникать деревни для защи^тй от непогоды и от врагов-хищников. Немало таких нео

литических поселений раскопано. По их остаткам видно, как постепенно развивались такие простейшие ремесла, нак гончарное, ткацкое и плотничье. Существовали житницы, так что население могло, производя излишки, запасать продукты на зиму и на случай неурожая. Выпекали хлеб, варили пиво, в эпоху позднего неолита плавили и обрабатывали медь и бронзу. Совершались открытия, были изобретены гончарный круг и тележное колесо, совершенствовались лодки и жилища. Все эти замечательные новшества возникали лишь в пределах той или иной зоны и не всегда распространялись вне ее. Например, американские индейцы узнали о существовании тележного колеса лишь после прихода белых. Тем ие менее теми технического прогресса в колоссальной мере ускорился по сравнению с древним каменным веком.

Деревни вели между собой значительную торговлю, которая настолько развилась, что можно проследить наличие торговых связей между областями, удаленными на сотни километров друг от друга. Эту коммерческую деятельность сильно стимулировали открытие техники выплавки меди и бронзы и изготовление сначала медных, а затем бронзовых орудий и оружия. Это в свою очередь содействовало дальнейшему формированию языков. Слова этих языков выражали вполне конкретные вещи и весьма немногочисленные абстрактные понятия, но языки уже имели известный запас слов для простых числовых терминов и для некоторых пространственных образов. На таком уровне находились многие племена в Австралии, Америке и Африке, когда они впервые встретились с белыми людьми, а некоторые племена и сейчас живут в таких условиях, так что есть возможность изучить их обычаи и способы выражения мыслей.

2. Числовые термины, выражающие некоторые из «наиболее абстрактных понятий, какие в состоянии создать человеческий ум», как сказал Адам Смит, медленно входили в употребление. Впервые они появляются скорее как качественные, чем количественные термины, выражая различие лишь между одним (или, вернее, «какимто»— «какойто» скорее, чем «один человек») и двумя и многими. Древнее качественное происхождение числовых понятий и сейчас еще выявляется в тех особых двоичных терминах, которые имеются в некоторых языках, как, например, в греческом и кельтском. С расширением понятия числа большие числа сначала образовывались с

помощью сложения: 3 путем сложения 2 и 1, 4 путем сложения 2 и 2, 5 путем сложения 2 и 3.

Вот примеры счета некоторых австралийских племен:

Племя реки Муррей: 1 = энэа, 2 = петчевал, 3 = петчевалэнэа, 4 = петчевалпетчевал.

Камиларои: 1 = мал, 2 = булан, 3 = гулиба, 4 = буланбулан, 5 = булангулиба, 6 = гулибагулиба').

Развитие ремесла и торговли содействовало кристаллизации понятия числа. Числа группировали и объединяли в большие единицы, обычно пользуясь пальцами одной руки или обеих рук — обычный в торговле прием. Это вело к счету сначала с основанием пять, потом с основанием десять, который дополнялся сложением, а иногда вычитанием, так что двенадцать воспринималось как 10+2, а девять — как 10 — 1²). Иногда за основу принимали 20 — число пальцев на руках и ногах. Из 307 систем счисления первобытных американских народов, исследованных Илсом (W. С. Eels), 146 были десятичными, 106 — пятичными и пятичнымидесятичными, остальные — двадцатичными и пятичнодвадцатнчными. В наиболее характерной форме система с основанием двадцать существовала у майя в Мексике и у кельтов в Европе. Числовые записи велись с помощью пучков, зарубок на палках, узлов на веревках, камешков или ракушек, сложенных по пять в кучки,— приемами, весьма схожими с теми, к каким в давние времена прибегал хозяин постоялого двора, пользовавшийся бирками. Для перехода от таких приемов к специальным символам для 5, 10, 20 и т. д. надо было сделать лишь один шаг, и именно такие символы мы обнаруживаем в пользовании в начале писанной истории, на так называемой заре цивилизации.

Древнейший пример пользования бирками приходится на эпоху палеолита. Это — обнаруженная в 1937 г. в Вестонице (Моравия) лучевая кость молодого волка длиной около 17 сантиметров с 55 глубокими зарубками. Первые двадцать пять зарубок размещены группами по пять, за ними идет зарубка двойной длины, заканчивающая этот ряд, а затем с новой зарубки двойной длины

') Con ant L. The Number Concept.—N. Y., 1896.—P. 106— 107, с многими подобными примерами; см. также статью И. Г. Башмаковой и А. П. Юшкевича, указанную в библиографии в конце этой главы.

²) Eels W. С. Number Systems of North American Indians // Amer. Math. Monthly— 1913.— V. 20.— P. 293.

начинается новый ряд из зарубок¹). Итак, очевидно, что неправильно старое утверждение, которое мы находим у Якоба Гримма и которое часто повторяли, будто счет возник как счет на пальцах. Пальцевый счет, то есть счет пятками и десятками, возник только на известной ступени общественного развития. Но раз до этого дошли, появилась возможность выражать числа в системе счисления, что позволяло образовывать большие числа. Так возникла примитивная разновидность арифметики. Четырнадцать выражали как 10 + 4, иногда как 15 — 1. Умножение зародилось тогда, когда 20 выразили не как 10 + + 10, а как 2 X 10. Подобные двоичные действия выполнялись в течение тысячелетий, представляя собой нечто среднее между сложением и умножением, в частности в Египте и в доарийской культуре МохенджоДаро на Инде. Деление началось с того, что 10 стали выражать как «половину тела», хотя сознательное применение дробей оставалось крайне редким явлением. Например, у североамериканских племен известны только немногие случаи применения дробей, и почти всегда это только дробь ½, хотя иногда встречаются 1/3 и ¼ ²).

Любопытно, что увлекались очень большими числами, к чему, может быть, побуждало общечеловеческое желание преувеличить численность стада или убитых врагов; пережитки такого уклона заметны в библии и в других религиозных книгах.

[i] Происхождение и развитие счета вообще, систем счисления в частности, и связанное с этим развитие понятия натурального числа изложены Д. Стройном крайне кратко. Большой этнографический, археологический и филологический материал, который приходится привлекать при таких исследованиях, не позволяет дать вполне определенные ответы на все вопросы, но некоторые этапы

') Isis, 1938 —V. 28.—Р. 462—463; взято из London News IHustr. от 2.Х 1937. [См. также данные о предметах, найденных при раскопках палеолитической стоянки в Меяине (Черниговской области УССР), в книге: История отечественной математики, т. 1, с. 40.— Примеч. пер ]

²) Миллер (G. A. Miller) обратил внимание на то, что слова one half, semis, moitie, обозначающие (в английском, латинском, французском языках) половину, не имеют прямой связи со словами тех же языков, означающими 2 (two, duo, deux), в отличие 1/3, ¼,...(англ.: one third, one fourth,...); это, видимо, указывает на то, что понятие ½ возникло независимо от понятия целого числа. См. Nat. Math. Magazine, 1939.—V. 13.—P. 272, 24

и некоторые общие черты в развитии техники счета и понятия числа можно установить с высокой степенью достоверности. На русском языке этот круг проблем наиболее обстоятельно и вместе с тем компактно освещен в статье И. Г. Башмаковой и А. П. Юшкевича (см. библиографию в конце главы I). Интересные данные, указывающие па более раннее развитие числовых представлений (чем до сих пор предполагалось), собраны в статье: Фролов Б. А. Применение счета в палеолите и вопрос об истоках математики // Изв. СО АН СССР, сер. общ. наук.— 1965.— № 9, вып. 3.

3. Возникла и необходимость измерять длину и емкость предметов. Единицы измерения были грубы, п при этом часто исходили из размеров человеческого тела. Об этом нам напоминают такие единицы, как палец, фут (то есть ступня), локоть. Когда начали строить дома такие, как у земледельцев Индии или обитателей свайных построек Центральной Европы, стали вырабатываться правила, как строить по прямым линиям и под прямым углом. Английское слово «straight» (прямой) родственно глаголу «stretch» (натягивать), что указывает на использование веревки¹). Английское слово «line» (линия) родственно слову «linen» (полотно), что указывает на связь между ткацким ремеслом и зарождением геометрии. Таков был один из путей, по которому шло развитие математических интересов.

Человек неолита обладал также острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин и тканей, позже — обработка металлов вырабатывали представление о плоскостных и пространственных соотношениях. Должны были сыграть свою роль и танцевальные фигуры. Неолитические орнаменты радовали глаз, выявляя равенство, симметрию и подобие фигур. В этих фигурах могут проявляться и числовые соотношения, как в некоторых Доисторических орнаментах, изображающих треугольные числа; в других орнаментах мы обнаруживаем «священные» числа. Такого рода орнаменты оставались в ходу и в исторические времена. Прекрасные образцы мы виДим на дипилоновых вазах минойского и раннегреческого периода, позже — в византийской и арабской мозаике, в персидских и китайских коврах. Первоначально ранние орнаменты, возможно, имели религиозное или магическое

') Во многих странах людей, занимавшихся межеванием, называли «натягивателями веревки» (греческое «harpenodaptai», арабское «massah», ассирийское «masihanu»). См. Gandz S.— Quellen und Studien zur Geschichte der Mathematik.—1930.— Bd 1.— S. 255—277.

Этот орнамент встречается па иео литическоп керамике из Боснии и на предметах искусства древней Месопотамии

значение, но постепенно преобладающим стало их эстетическое назначение.

В религии каменного века мы можем уловить первые попытки вступить в борьбу с силами природы. Религиозные обряды были насквозь пронизаны магией, магический элемент входил в состав существовавших тогда числовых и геометрических представлений, проявляясь также в скульптуре, музыке, рисунке.

Существовали магические числа такие, как 3, 4, 7, и магические фигуры, как, например, пятиконечная звезда и свастика; некоторые авторы даже считают, что эта сторона математики была решающим фактором в ее развитии¹), но, хотя общественные корчи математики в новейшие времена, быть может, стали менее за

метны, они вполне очевидны в раппем периоде истории человечества. Современная «нумерология»—пережиток магических обрядов, восходящих к неолитической, а может быть, даже к палеолитической эпохе.

[2] Работы, авторы которых стремятся доказать ритуальное происхождение счета и хеометрии, появляются и в наши дни. Эти работы примыкают к тем течениям в социологии, которые стремятся всячески выпятить значение религии в истории человеческой культуры Одна из последние исследований такого рода — статья А Зайденбер! а «Ритуальное происхождение счета» (S e i d e пberg A. The Ritual Origin of Counting.—Archive for History of Exact Sciences.— 1962.—V. 2, N 1). Автор прямо заявляет, что рассматривает свою работу как частичное выполнение программы лорда Раглапа: доказать, что вся цивилизация — ритуального про

') McGee W. J. Primitive Numbers.—Nineteenth Annual Report, Bureau Amer. Ethnology, 1897—1898 (1900).—P. 825—851.

Такие орнаменты были в ходу у жителей свайных построек близ Любляны (Югославия) Гальштатского периода (Центральная Европа, 1000—500 до н. э.)

исхождения '). По Зайденбергу, счет был изобретен при особых обстоятельствах в связи с созданием определенного ритуала. Но большое сходство в построении числительных и приемах счета у различных народов делает версию совершенно неправдоподобной (поскольку она связывает счет с весьма специфическими приемами), если не допустить, что счет был изобретен таким образом в какомто одном месте и уже оттуда распространился путем заимствования по всему миру. И. А. Зайдевберг не отступает перед этим выводом и в особой работе, напечатанной в «Математических

Эти прямоугольники, заполненные треугольниками, и треугольники с кружками воспроизведены с урн из захоронений вблизи Шопрона в Венгрии Мы видим здесь попытку образовать треуюльные числа, игравшие важную роль позже — в пифагорейской математике

сообщениях Калифорнийского университета» за 1960 г.²), пытается его доказать. Насколько невероятно то, что счет у всех народов общего происхождения, читатель может судить сам, если вспомнит о ра юбщеппости первобытных общин, о значительной неравномерности в развитии счета у различных народов, о наличии у одного и того же народа различных слов для обозначения одного и того же числа различных предметов и т. д.

4. Даже у самых отсталых племен мы находим какой-то отсчет времени и. следовательно, какието сведения о движении Солнца, Луны и звезд. Сведения этого рода впервые приобрели более научный характер, когда стали развиваться земледелие и торговля. Пользование лунным календарем относится к очень давней эпохе в истории

') Lord Raglan. How Came Civilisation.

²) University of California Mathematical Publications.— V. A3, N4

человечества, так как изменение в ходе произрастания растений связывали с фазами Луны. Примитивные народы обратили внимание и на солнцестояние, и на восход Плеяд в сумерках. Самые древние цивилизованные народы относили астрономические сведения к наиболее отдаленному, доисторическому периоду своего существования. Другие первобытные народы пользовались при плавании созвездиями как ориентирами. Эта астрономия дала некоторые сведения о свойствах сферы, окружностей, об углах.

5. Эти краткие сведения из эпохи зарождения математики показывают, что наука в своем развитии не проходит обязательно все те этапы, из которых теперь складывается ее преподавание. Лишь недавно ученые обратили должное внимание на некоторые из древнейших известных человечеству геометрических фигур такие, как узлы или орнаменты. С другой стороны, некоторые более элементарные ветви нашей математики, как построение графиков или элементарная статика, сравнительно недавнего происхождения. А. Шпайзер заметил с известной едкостью: «За позднее происхождение элементарной математики говорит хотя бы то, что она явно склонна быть скучной,— свойство, видимо, ей присущее,— тогда как творческий математик всегда предпочтет заниматься задачами интересными и красивыми»¹).

[3] Это суждение А. Шпайзера, известного как своими работаМи по теории групп, так и трудами по изданию полпого собрания сочинений Леонарда Эйлера, остроумно и парадоксально, но вряд ли можно его отстаивать всерьез И в книге по истории математики надо оговорить содержащиеся в нем погрешности против истории.

Что такое элементарная математика? Общепринятого определения нет, содержание этого понятия, несомненно, менялось. Если

') Sреiser A. Theorie der Gruppen von endlicher Ordnung — Leipzig, 1925, N. Y., 1954.—P. 3.

к элементарной математике отнести материал, входящий в курс средней школы» (что тоже далеко не однозначно характеризует элементарную математику), то нетрудно убедиться в крайней разнородности отдельных ее частей. В арифметике, кроме обучения счету, мы встречаем решение задач с использованием приемов, большей частью достаточно давнего происхождения, и некоторый сведения из теории целых чисел, которые в большинстве восходят к античной математике. И геометрия до недавнего времени в течение столетий излагалась в основном по Евклиду. В алгебре и тригонометрии основной материал гораздо более недавнего происхождения, причем некоторые понятия и приемы (графики, функциональная зависимость) в значительной мере модернизованы. «Скучен» ли он? Для обучаемого это зависит от того, как ведется обучение, для обучащего — от того, есть ли тут возможность для творчества, не обязательно научного, а педагогического, методического. Многочисленные предложения реформы школьных программ, настойчивые попытки ввести в курс средней школы некоторые сведения из математического анализа, математической логики, теории вероятностей и т. п. показывают, что здесь есть немалое поле для интересной деятельности.

Элементарную математику пытались определять отрицательно, как часть математики, где не применяются такието (более сложные) методы и понятия, например, где не пользуются математическим анализом (дифференциальным и интегральным исчислением). Но при этом в элементарную математику попадут многие достаточно отвлеченные и трудные области, которые привлекали и привлекают творческих математиков и где есть немало «интересных и красивых задач»1), например значительная часть теории множеств, теории групп, математической логики. Нетрудно также привести примеры, когда так называемое элементарное доказательство того или иного положения находили позже и с большим трудом, чем неэлементарные.

ЛИТЕРАТУРА

Кроме уже упомянутых книг Конанта, Илса, Смита и Шпайзера, укажем еще:

Feltweis E. Das Rechen der Naturvolker.— Leipzig, 1927.

Menninger K. Zahlwort und Ziffer. Eine Kulturgeschichle der Zahlen.— 2 Aufl.— Bd 1.— Gottingen, 1957. 2 Aufl.— Bd 2 (Zahlschrift und Rechnen).—Gottingen, 1958.

Smith D. E., Ginsburg J. Numbers and Numerals.— N. Y. Teacher' College, 1937.

Childe Gordon. What Happened in History.— Harmondsworth; N. Y.: Pelican Book, 1942.

Интересные арпаменты описаны в работах:

Spier L. Plains Indian Parfleche Designs // Univ. Washington Publ. in Anthrop.— 1931.—V. 4.—P. 293—322.

Deacon A. B. Geometrical Drawings from Malekula and Other Islands fo the New Hebrides // J. Roy. Anthrop. Inst—1934.— V. 64.— P. 129—175.

Pоpоva M. La geometric dans la broderie bulgare / Comptes Rendus, Premier Congres des Mathematiciens des pays slaves, Warsaw, 1929.— P. 367—369.

') Не говоря уже о том, сколько субъективного связано с такими определениями.

Математика американских индейцев рассматривается в статье: Тhоmpsоn J.E.S. Maya Arithmetic // Contribution to Amer Anthropology and History.1941.V. 36.Carnegie Inst, of Washington Publ.— P. 37—62.

Подробную библиографию см. в книге:

Smith D. E. History of Mathematics.— V. 1.— Boston, 192.3.—P. 14.

См. также:

Piaget J. La genese du nombre chez 1'enfant.— Neufchatel, 1941

Piaget J. Le developpement des quantites chez 1'enfant— Neufchatel, 1941.

На русском языке см.: Башмакова И. Г., Юшкевич А. П. Происхождение систем счисления // Энциклопедия элементарной математики, т. I.— M.; Л.: Гостехиздат, 1951,—С. 11—74.

Глава II

ДРЕВНИЙ ВОСТОК

1. В течение пятого, четвертого и третьего тысячелетия до н. э. новые и более совершенные формы общества складывались на основе упрочившихся общий нового каменного века, существовавших на берегах великих рек Африки и Азии в субтропическом поясе и вблизи него. Эти реки — Нил, Тигр и Евфрат, Инд, позже — Ганг, Ху анхэ, еще позже — Янцзы.

Прибрежные земли в районах этих рек могли давать обильные урожаи при условии регулирования разливов и осушения болот. В противоположность бесплодным пустыням и горным областям и равнинам, примыкавшим к этим речным долинам, последние можно было сделать райским местом. И в течение столетий такую задачу удалось решить путем постройки валов и плотин, создания сети каналов и водохранилищ. Регулирование водоснабжения потребовало совместных усилий населения обширных районов в размерах, значительно превосходивших то, что предпринималось в этом роде раньше. Это повело к установлению централизованного управления, сосредоточенного в городских центрах, а не в варварских селенияк предшествующих эпох. Сравнительно большие излишки, которые давало значительно усовершенствованное и интенсивное земледелие, повысили уровень жизни населения в целом, заодно это создало городскую аристократию во главе с могущественными вождями. Возникло немало профессий и специальностей — их представляли ремесленники, солдаты, писцы и жрецы. Руководство общественными рабогами находилось в руках бессменных должносшых лиц — группы людей, сведущих в смене времен года, движении небесных тел, в деле землеустройства, хранения запасов пищи и взимания налогов. Пользовались письменностью, чтобы придать форму закона требованиям администрации и действиям правителей.

Чиновники, равно как и ремесленники, накопили значительный запас технических знаний, включая сюда металлургию и медицину. В состав этих знаний входило и искусство счета и измерения.

Теперь уже прочно сложились общественные классы. Это были вожди («цари»), самостоятельные землевладельцы и арендаторы, ремесленники, писцы и чиновники, крепостные и рабы. Местные вожди стали настолько богаче и сильнее, что их уже нельзя было считать чемто вроде феодалов с ограниченной властью, — они становились вполне самодержавными царями Раздоры и войны между различными деспотами приводили к возникновению более обширных владений, управляемых единым монархом. Так эти общественные формы, в основе которых лежало орошаемое и интенсивное земледелие, дали некий «восточный» вид деспотизма. Такой деспотизм мог держаться столетиями и затем пасть, то ли под ударами горных племен или кочевников пустыни, привлеченных богатствами речной долины, то ли изза того, что запущенной оказывалась обширная, сложная и жизненно необходимая оросительная система. При таких обстоятельствах власть в племени либо переходила от одного царя к другому, либо же сообщество распадалось на меньшие объединения, причем процесс слияния мог затем начаться заново. Впрочем, при всех этих династических переворотах и повторных переходах от раздробленности к абсолютному деревни, составлявшие основу этого общества, собственно оставались незатронутыми и, стало быть, экономический и общественный строй в основном сохранялся. Восточное общество жило циклами, и даже сейчас в Азии и Африке есть много общин, сохранявших в течение тысячелетий один и тот же уклад жизни. В этих условиях продвижение вперед было медленным и извилистым, и периоды культурного подъема разделялись столетиями застоя и упадка.

Такая статичность Востока создавала некую исконную освященность его установлений, и это облегчало отождествление церкви и государственного аппарата. Чиновничество в значительной своей части было религиозного склада, как и государство в целом; во многих восточных странах жрецы были правителями областей. А так как заниматься наукой было задачей чиновничества, то во многих (но не во всех) восточных странах жрецы занимали выдающееся положение как обладатели научных знании.

2. Восточная математика возникала как прикладная наука, имевшая целью облегчить календарные расчеты₎ распределение урожая, организацию общественных работ и сбор налогов. Вначале, естественно, главным делом били арифметические расчеты и измерения. Однако в науке, которую столетиями культивировали специалисты, чьей задачей было не только ее применение, но и посвящение в ее тайны, должен был развиться абстрактный уклон. Постепенно наукой стали заниматься ради нее самой. Из арифметики выросла алгебра не только потому, что это облегчало практические расчеты, но и в результате естественного развития науки, культивируемой и совершенствуемой в школах писцов. В силу тех же причин из измерений возникли начатки (но не больше) теоретической геометрии.

Хотя торговля и процветала в этих обществах древнего Востока, их экономическая сердцевина оставалась земледельческой, хозяйственной основой были села, обособленные и консервативные. Это приводило к тому, что различные культуры оставались резко отличными одна от другой, вопреки сходству экономического строя и одинаковому в основном уровню научных сведений. Замкнутость китайцев и египтян вошла в поговорку. Никогда не составляло труда отличить друг от друга искусство и письменность Египта, Месопотамии, Китая, Индии. Точно так же мы можем говорить о египетской, месопотамской, китайской и индийской математике, хотя в общем по своей арифметико-алгебраической природе они весьма схожи. Даже если наука одной из этих стран в течение некоторого периода обгоняла науку другой, она сохраняла свойственные ей приемы и символику.

На Востоке трудно датировать новые открытия. Статический характер его общественного строя приводил к тому, что научные сведения сохранялись без изменений в течение столетий и даже тысячелетий. Открытия, сделанные в пределах одного городского поселения, могли остаться неизвестными в других местностях. Хранилища научных и технических знаний могли быть уничтожена войнами при смене династий, наводнениями. Предание гласит, что в 221 г. до н. э., когда один абсолютный деспот Цинь Шихуанди (династии Цинь, Первый Желтый император) установил свое господство над всем Китаем он приказал уничтожить все научные книги. Позже многое было вновь записано по памяти, но подобные события весьма затрудняют датировку открытий.

Другая трудность в датировке достижений восточной яауки связана с материалом, которым пользовались для их закрепления. Народы Двуречья обжигали глппяные таблички, которые практически были неразрушимы¹). Египтяне пользовались папирусом, и поэтому значительная часть памятников их письменности сохранилась в условиях сухого климата. Китайцы и индийцы применяли значительно менее надежный материал — древесную кору пли бамбук. Китайцы во втором столетии н. э. начали пользоваться бумагой, но мало что сохранилось от тысячелетия, предшествующего семисотому году н. э. Поэтому наши сведения о восточной математике весьма отрывочны, и для столетий догреческой эпохи мы, кроме материалов Египта и Двуречья, почти ничем не располагаем. Вполне возможно, что новые открытия поведут к полной переоценке относительного значения различных форм восточной математики. В течение долгого времени самыми богатыми историческими источниками мы обладали по Египту благодаря открытому в 1858 г. так называемому папирусу Райнда (Rhind), написанному около 1650 г. до н. э., но содержащему значительно более старый материал. За последние двадцать лет наши сведения о вавилонской математике значительно возросли благодаря замечательным открытиям О. Нейгебауера и Ф. Тюро-Данжена, которые расшифровали большое число глиняных табличек. Теперь выясняется, что вавилонская математика была значительно более развита, чем ее восточные партнерши. Возможно, это заключение будет окончательным, так как существует известное соответствие в содержании вавилонских и египетских текстов за ряд столетий. Более того, в экономическом развитии Двуречье ушло дальше, чем другие страны так называемого плодородного пояса на Ближнем Востоке, простиравшегося от Двуречья до Египта. Двуречье было перекрестком многочисленных караванных путей, тогда как Египет находился сравнительно в стороне. К этому надо добавить то обстоятельство, что возделывание почвы в районе блуждающих Тигра и Евфрата требует больше технического искусства и регулировки, чем в районе Нила, этой «самой добропорядочной из всех рек», если воспользоваться выражением Уильяма Уилкокса. Быть может, дальнейшее изуче

') Если только их тщательно сберегать после того, как они откопаны. Много табличек пропало изза плохого обращения с ними.

Страница из папируса Райнда

ние древнеиндийской математики обнаружит неожиданные достижения, но пока притязания на это не кажутся достаточно обоснованными.

3. Источником большей части наших сведений об египетской математике являются два математических папируса. Один из них – это уже упомянутый папирус Райнда, содержащий 84 задачи, второй – так называемый московский папирус, который, может быть, на два столетия старше и содержит 25 задач. Эти задачи были уже достаточно

стары, когда составлялись папирусы, но есть меиьшие папирусы значительно более позднего происхождения, даже римских времен, которые не отличаются от названных по своим приемам. Математика, которая в них изложена, основана на десятичной системе счисления со специальными знаками для каждой десятичной единицы более высокого разряда — системе, которая нам знакома благодаря римским обозначениям, основанным па том же принципе: MDCCCLXXVIII= 1878. На основе такой системы египтяне построили арифметику преимущественно аддитивного характера, т. е. ее основное направление состоит в сведении всех умножений к повторным сложениям. Например, умножение на 13 получается умножением сначала на 2, затем на 4, затем на 8 и сложением результатов умножения на 4 и на 8 с первоначальным числом:

Например, для вычисления 13*11 писали:

*1 11

2 22

*4 44

*8 88

и складывали все числа, отмеченные звездочкой, что дает 143.

Самой замечательной чертой египетской арифметики являются действия с дробями. Все дроби сводятся к суммам так называемых основных дробей, то есть дробей, имеющих числителем единицу. Единственное исключение составляла дробь 2/3=1 — 1/3, для которой существовал специальный символ. Сведение к суммам основных дробей производилось с помощью таблиц, которые давали разложение дробей вида 2/n — единственное необходимое разложение, так как умножение было двоичным. Папирус Райнда дает таблицу, в которой приведены разложения па основные дроби для всех нечетных n от 5 до 331, например

2/7=1/4+1/28,

2/97=1/56+1/679+1/776

Из чего исходили при таком сведении к основным дробям, не ясно (например, почему 2/19 заменяется суммой 1/12+1/76+1/114, а не суммой 1/12+1/57+1/228?)

Такие действия с дробями придавали египетской математике тяжеловесность и растянутость, однако разложение на сумму основных дробей применялось в течение тысячелетий, не только в эпоху эллинизма, но и в средние века. В то же время указанное разложение предполагает определенное математическое искусство, и существуют интересные теории для объяснения того способа, каким египетские специалисты могли получить свои результаты').

Многие задачи очень просты и сводятся к линейному уравнению с одним неизвестным:

Некое количество, его 2/3, его 1/2 и его 1/7, сложенные вместе, дают 33. Каково это количество?

Ответ: 14 28/97, записан в основных дробях: 14+1/4+1/97+1/56+1/679 +1/776+1/194+1/388. Для неизвестного в уравнении существовал иероглиф, обозначавший «кучу» и произносившийся «хау» или «аха». Поэтому египетскую алгебру иногда называют «хау-исчислением»

В задачах речь идет о количестве хлеба и различных сортов пива, о кормлении животных и хранении зерна, и это указывает на практическое происхождение такой запутанной арифметики и примитивной алгебры. В некоторых задачах проявляется теоретический интерес, например в задаче, в которой требуется разделить сто хлебов между пятью людьми так, чтобы их доли составляли арифметическую прогрессию и чтобы одна седьмая суммы трех больших долей была равна сумме двух меньших. Мы даже встречаем геометрическую прогрессию в задаче о семи домах, в каждом из которых есть семь кошек, каждая из которых поедает семь мышей и т. д., что выявляет знание формулы для суммы членов геометрической прогрессии.

^l)Neugebauer О. Arithmeiik und Rechnentechmlc dm Agypler / Quellen und Studien zur Geschichte der Malheraatik.1931.—Bd 1.— S. 301380; van der Waerden B. L. Die Entwickiungsgeschichte der agyptischen Bruchrechnung // Quelleu und Studien zur Geschichte der Mathematik.— 1938.— Bd 41.— P. 359—382; Яновская С. А. К теории египетских дробей / Тр. Ин-та истории естествознания.— 1947,— Т. 1,—С. 269—282; Веселовский И.Н. Египетская наука и Греция / Тр Ин-та истории естествознания.1948.—Т. 2.—С. 426—428; см также Bruins Е. M.Proc. Nederl. Akad. Wet.—1952.V. А55.

Некоторые задачи имеют геометрическую природу и касаются преимущественно измерений. Площадь треугольника находится как половина произведения основация и высоты; площадь круга диаметра d определяется как (d-d/ 9)², что дает для pзначение 256/81≈3,1605. Мы находим также некоторые формулы для объемов тел, таких, как куб, параллелепипед и круговой цилиндр, причем все они рассматриваются конкретно как сосуды, преимущественно для зерна. Самым замечательным результатом в египетских измерениях была формула для объема усеченной пирамиды с квадратным основанием V=h/3(a²+ab+b²), где a и b суть длины сторон квадратов, a h— высота. Этот результат, которому не найдено соответствующего ни в какой другой древней математике, особенно примечателен, поскольку нет указаний на то, чтобы египтяне имели какое-либо представление даже о теореме Пифагора, вопреки некоторым необоснованным рассказам о гарпедонафтах, которые якобы строили прямые углы с помощью веревки, имевшей 3 + 4 + 5=12 узлов').

Мы здесь должны предостеречь от преувеличения древности египетской математической науки. Строителям пирамид эпохи 3000 лет до н. э. и даже раньше приписывали всевозможные результаты высокоразвитой науки. Существует даже много раз серьезно преподносившаяся версия, будто египтяне в 4212 г. до н. э. приняли так называемый сотический цикл для календаря. Нельзя всерьез приписывать столь точные математические и астрономические работы народу, едва вышедшему из условий каменного века, и источником таких рассказов, как обычно удается установить, является позднее египетское предание, дошедшее до нас через греков. Общей чертой древних цивилизаций является стремление датировать главные сведения весьма ранними эпохами. Все доступные тексты указывают, что египетская математика была скорее примитивного характера. На таком же уровне находилась и их астрономия.

4. Переходя к математике Двуречья, мы оказываемся на гораздо более высоком уровне, чем тот, которого ког

') См Gandz S. // Quellea and Studien zur Geschichte der Malhematik. 1930 Bd 1 S. 7.

да-либо достигала египетская математика. Здесь мы можем даже уловить прогресс в ходе столетий. Уже самые древние тексты, относящиеся к последнему шумерскому периоду (третья династия Ура, 2100 г. до н. э.), показывают высокое вычислительное искусство. Эти тексты содержат таблицы для умножения, в которых хорошо развитая шестидесятичная система счисления сочетается с более ранней десятичной системой; здесь имеются клинописные символы, обозначающие 1, 60, 360 и также 60^-1, 60^-2. Однако не это было наиболее характерной их чертой. В то время как египтяне каждую единицу более высокого разряда обозначали новым символом, шумеры пользовались одним и тем же символом, но указывали его значение его положением. Так, 1, за которой следовала другая 1, давала запись числа 61, а 5 с последующим 6 с последующим 3 (мы это будем записывать как 5, 6, 3) обозначало 5•60²+6•60+3 = 18363. Такая позиционная (или поместная) система не отличается, по сути дела, от нашей системы записи чисел, при которое символ 343 заменяет 3•10² + 4•10+3. Подобная система имеет огромное преимущество при вычислениях, что можно сразу увидеть, если попытаться выполнить умножение и в нашей системе, и в системе с римскими цифрами. Позиционная система устраняла многие трудности в арифметике дробей так же, как это происходит при нашей системе с введением десятичных дробей. По-видимому, вся эта система была непосредственным результатом развития техники управления, что засвидетельствовано в тысячах текстов того же периода, где речь идет о поставках скота, зерна и т. п. и о связанных с этим арифметических вычислениях.

При таком способе счета существовала некоторая неопределенность, так как значение символа не всегда было ясно по его положению. Так, (5, 6, 3) могло также означать 560¹ +6•60°+ 3•60^-1=306 1/20, и точное исстолкование надо было извлечь из контекста. Другая неопределенность возникала из-за того, что незаполненное место иной раз означало нуль, так что (11,5) могло стоять вместо 11•60² +5=39605. Иной раз появляется специальный символ для нуля, но не ранее персидской эпохи. Так называемое «изобретение нуля» было, таким образом, логическим следствием введения поместной системы, но только после того, как техника вычислений была значительно усовершенствована.

Оборотная сторона древневавилонской таблички, хранящейся в Эрмитаже (Эрм. 15073). Вероятно, XVII в. до н. э.

Как шестидесятатаая система, так и позиционность и системы счисдеевия оказались прочиым достоянием человечества. Наше современное деление часа на 60 минут и 3600 секунд восходит к шумерам, равно как и наше деление окружности на 360 градусов, каждого градуса на 60 минут и каждой минуты на 60 секунд. Есть основания полагать, что выбор в качестве основы 60 вместо 10 появился при попытке унифицировать системы измерения, хотя то обстоятельство, что 60 имеет много делителей, тоже могло иметь значение. Что касается поместной системы, непреходящее значение которой сравнивают со значением алфавита'), так как оба изобретения заменя

')Neugebauer О The History of Ancient Astronomy // Journal of Near Eastern Studies.— 1945,— V. 4.— P. 12.

ют сложную символику методом, легко доступным широкому кругу людей, то ее история в значительной мере еще темна. Есть основание предполагать, что как индийцы, так и греки познакомились с нею на караванных путях, которые вели через Вавилон. Нам известно также, что арабы говорили о ней как об индийском изобретении. Однако вавилонская традиция могла повлиять на все позднейшее распространение поместной системы.

5. Следующая группа клинописных текстов относится ко времени первой вавилонской династии, когда в Вавилоне правил царь Хаммурапи (около 1950 г. до н. э.) и семитское население подчинило себе исконных жителей — шумеров. В этих текстах мы видим, что арифметика развилась в хорошо разработанную алгебру. Египтяне того же периода были в состоянии решать только простые линейные уравнения, а вавилоняне времен Хаммурапи полностью владели техникой решения квадратных уравнений. Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и к биквадратным уравнениям. Такие задачи они формулировали только при определенных числовых значениях коэффициентов, но их методы не оставляют никакого сомнения относительно того, что они знали общие правила.

Приведем пример, взятый из одной из глиняных табличек этого периода.

«Площадь А, состоящая из суммы двух квадратов, составляет 1000. Сторона одного из квадратов составляет 2/3 стороны другого квадрата, уменьшенные на 10. Каковы стороны квадратов?»

Это приводит к уравнениям х² + y ² =1000, у=2/3• x — 10, решение которых сводится к решению квадратного уравнения

13/9 x²–40/3 x –900=0

имеющему положительный корень х = 30.

В действительности решение в клинописном тексте ограничивается, как и во всех восточных задачах, простым перечислением этапов вычисления, необходимого для решения квадратного уравнения:

«Возведи в квадрат 10; это дает 100; вычти 100 из 1000; это дает 900» и т.д.

Резко выраженный арифметико-алгебраический характер вавилонской математики проявляется и в геометрии. Как и в Египте, геометрия развивалась на основе практических задач измерения, но геометрическая форма

задачи обычно является только средством для того, чтобы поставить алгебраический вопрос. Предыдущий пример показывает, как задача относительно площади квадрата приводит к нетривиальной алгебраической проблеме, и этот пример не составляет исключения. Тексты показывают, что вавилонская геометрия семитского периода располагала формулами для площадей простых прямолинейных фигур и для объемов простых тел, хотя объем усеченной пирамиды еще не был найден. Так называемая теорема Пифагора была известна не только для частных случаев, но и в полной общности. Основной чертой этой геометрии был все же ее алгебраический характер. Это в равной мере относится и ко всем позднейшим текстам, особенно к текстам третьего периода, от которого до нас дошло немалое их число,— эпохи нововавилонской, персидской и эпохи Селевкидов (примерно от 600 г. до н. э. до 300 г. н. э.). Тексты этого последнего периода обнаруживают значительное влияние вавилонской астрономии, которая в это время приобретает характер настоящей науки, что сказывается в тщательном анализе различных эфемерид. Вычислительная техника математических текстов становится еще более совершенной; алгебра справляется с задачами на уравнения, для которых требуется значительное вычислительное искусство. От эпохи Селевкидов дошли вычисления, которые доведены до семнадцатого шестидесятичного знака. Столь сложные вычислительные работы уже нельзя связывать с вычислением налогов или измерением — стимулом для них были астрономические задачи или просто любовь к вычислениям.

Многое в этой вычислительной арифметике выполнялось с помощью таблиц, в наборе которых есть и простые таблицы для умножения, и таблицы обратных величин, квадратных и кубических корней. В одной из таблиц имеется ряд чисел вида п³ + п², которым, повидимому, пользовались для решения кубических уравнений вида х³ + х² = а. В них содержатся некоторые превосходные приближения: √2≈ дается 1 5/12 (√2≈1.4142, 1 5/12≈ 1.4167)¹), для 2/√2≈0.7071 дается 17/24≈0.7083. Видимо, квадратные корпи определялись по формуле

') Neugebauer О. Exact Sciences in Antiquity //Univ. of Pennsylvania Bicentennial Conference, Studies in Civilization, Philadelphia, 1941.— P. 13—29.

наподобие следующей:

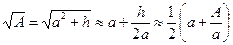
Что касается значения p, в большинстве случаев таблички обходятся библейским p=3. Есть указания на то, что применялись и лучшие приближения, дававшие для p значение 3 1/8 ¹).

Уравнение х³+х^г=а появляется в задаче, в которой требуется решить систему уравнений xyz + ху = 1 + 1/6, y=2/3 x, z=12x, что сводится к уравнению

(12 x)³+(12 x)²=252

или, согласно таблицам, 12х = 6.

В клинописных текстах есть задачи и на сложные проценты. Например, ставится вопрос, за какое время удвоится сумм