Динамика простейшего ротора

III. ВИБРАЦИЯ И УДАР

КОЛЕБАНИЯ РОТОРОВ

Динамика простейшего ротора

Рассмотрим изгибные колебания простейшего ротора, состоящего из невесомого вала, на котором закреплён диск массой m (рис. 13.1).

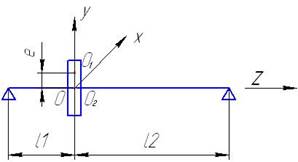
Рис. 13.1. Простейший ротор

Вал вращается на 2-х шарнирных опорах. Допустим, что опоры абсолютно жесткие, и диск расположен посередине вала (). Точку пересечения оси вала со срединной плоскостью диска (точку крепления диска к валу) обозначим О₂. Смещение этой точки будет являться прогибом вала в месте расположения диска. Будем считать, что центр масс диска расположен в точке О₁ и смещён относительно оси вала (точки О₂) на величину эксцентриситета e. Будем рассматривать только изгибные колебания ротора. Колебания ротора будем рассматривать в глобальной системе координат OXYZ, начало которой расположено на недеформируемой оси опор в точке ее пересечения со срединной плоскостью диска.

Ось Z совпадает с осью опор и направлена так, как это показано на рисунке, оси X, Y находятся в срединной поверхности диска (X – горизонтально; Y – вертикально).

Прогиб вала, т.е. смещение точки О₂ от оси недеформируемого вала будем обозначать как 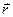. Проекции этого вектора на оси будем обозначать как , .

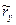Здесь и далее знак «~» обозначает, что данная величина является функцией от времени.

Опоры ротора могут деформироваться, и в этом случае точка О₂ будет смещаться не только за счёт прогиба вала, но и за счёт опор. Полное смещение точки О₂ будем описывать вектором 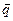. Проекции этого вектора на оси обозначим как 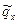и .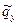

В рассматриваемом случае опоры являются абсолютно жёсткими: .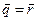

Смещение центра масс диска (точки О₁) от оси опор будем обозначать вектором 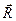. Его проекции соответственно: .

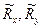Поскольку центр масс диска смещён относительно оси, то говорят, что имеет место массовая неуравновешенность. Из-за ее наличия при вращении ротора с угловой скоростью 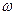возникает центробежная сила, в результате действия которой вал деформируется. Это приведёт к тому, что вал начнёт не только вращаться относительно своей оси, но и совершать круговое движение вокруг оси опор.

Примем, что в начальный момент времени (t=0) точка О₁ располагалась в горизонтальной плоскости, т.е. находилась на оси Х. В произвольный момент времени t точки О₁ и О₂ расположены так, как показано на рисунке 13.2.

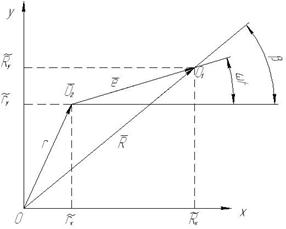
Рис. 13.2. Колебания ротора в плоскости ОXY

Из рисунка находим:

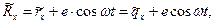(13.1)

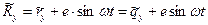. (13.2)

Запишем условие равновесия для диска:

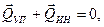(13.3)

Здесь 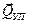- сила упругости, возникающая в вале при его прогибе; 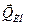- сила инерции.

Сила упругости зависит от прогиба вала и от жесткости вала c:

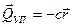(13.4)

Сила инерции в соответствии с принципом Даламбера

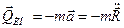, (13.5)

Подставив (13.4) и (13.5) в (13.3) с учетом (13.1) и (13.2), получим:

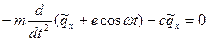(13.6)

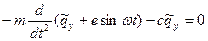. (13.7)

Разделим все слагаемые уравнений (13.6), (13.7) на массу m, введем обозначение 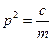(это собственная частота колебаний вала) и продифференцируем по t. Получим:

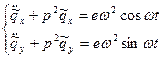(13.8)

Решение системы (1.8) имеет вид:

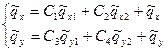(13.9)

Здесь 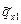, , 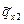, 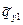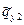- любые линейно независимые частные решения однородной системы дифференциальных уравнений

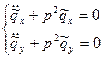, (13.10)

С_1…4 – неизвестные постоянные, которые определяются из начальных условий, 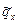, 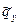- любые частные решения неоднородной системы (13.8).

В соответствии с этим можно записать решение (13.9) в виде:

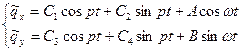. (13.11)

Первые два слагаемых в каждом решении описывают свободные колебания вала, которые происходят с собственной частотой вала p и быстро затухают вследствие трения. Поэтому будем рассматривать только вынужденные колебания с частотой 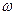, представленные третьими слагаемыми.

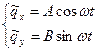(13.12)

Подставим (13.12) в (13.8). Получим:

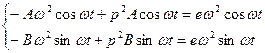. (13.13)

Отсюда 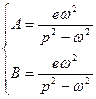, (13.14)

и колебания ротора будут описываться выражениями

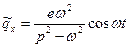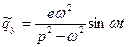; . (13.15)

Проследим за движением ротора в течение промежутка времени, за который вал совершит один полный оборот вокруг своей деформированной оси. Примем, что в момент начала наблюдения t=0. Тогда за указанный промежуток времени фаза колебаний 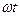изменится от 0 до 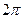. Положение сечения вала для различных значений фазы колебаний изображено на рис. 13.3. Видно, что за один полный оборот вокруг деформированной оси вал также совершит один полный оборот вокруг оси опор.

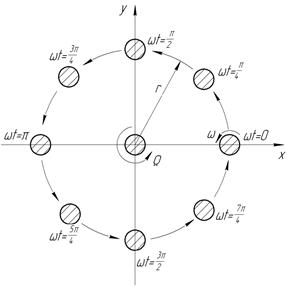
Рис. 13.3. Прецессия ротора

Вращение вала относительно своего положения равновесия называется прецессионным движением, или прецессией ротора. Частоту прецессионного вращения будем обозначать 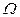. В рассматриваемом случае частота прецессии равна частоте вращения вала вокруг своей оси, т.е.

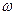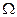= (13.16)

В общем случае 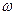и 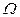могут не совпадать как по величине, так и по направлению. При соблюдении условия (13.16) прецессия называется синхронной. Есл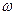и и 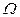совпадают по направлению, то прецессия называется прямой, а если прецессионное движение и вращение вала происходит в разные стороны, то прецессия называется обратной.

Определим прогиб вала.

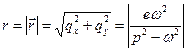. (13.17)

Как видно, он является постоянным и не зависит от времени, то есть прецессионное движение происходит по окружности. Прецессия с постоянной амплитудой и угловой скоростью называется регулярной.

Видно, что при 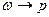происходит 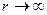. Резонансное увеличение амплитуды колебаний будет продолжаться до тех пор, пока вся энергия колебаний не будет уходить на преодоление сил трения, или пока вал не разрушится. Частота вращения ротора, на которой он вступает в резонанс, называется его критической частотой вращения.

Рассмотрим, что происходит с центром масс ротора при прохождении резонанса. В соответствии с формулами (13.1) и (13.2)

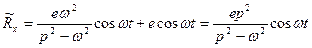(13.18)

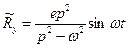. (13.19)

Из (13.18), (13.19) видно, что 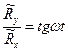; из (13.15) видно, что также .

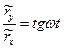Т.о. точки О₁ и О₂ расположены на одной прямой.

Если 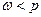, то 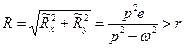(рис.13.4).

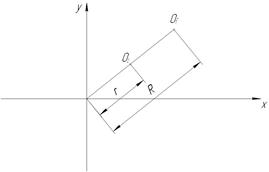
Рис. 13.4. Колебания ротора при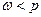

Если 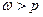, то 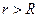(рис. 13.5).

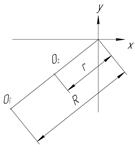
Рис.13.5. Колебания ротора при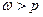

Если 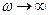, 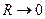. Это явление называется самоцентрированием ротора.

В рассмотренной расчетной схеме вал имеет только одну степень свободы (прогиб диска). Реальный ротор ГТД имеет бесконечное множество степеней свободы, а следовательно, собственных частот колебаний и критических вращения. Низшую из них называют первой критической частотой вращения, следующую по возрастанию – второй, и так далее. Критические частоты будем обозначать как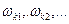

Форма колебаний – это относительное распределение перемещений по колеблющемуся телу. Каждой критической частоте соответствует одна и только одна форма колебаний (рис. 13.6). Точки, в которых амплитуда колебаний равна нулю, называются узловыми.

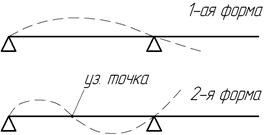
Рис.13.6. Колебания ротора на жестких опорах.

Амплитуда колебаний зависит от соотношения силы, вызывающей колебания (в данном случае, центробежная сила, зависящая от массы ротора, эксцентриситета и угловой скорости вращения) и силы трения. Однако соотношения амплитуд между собой сохраняются для каждой формы колебаний (рис. 13.7).

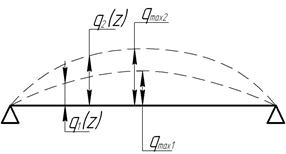
Рис. 13.7. Первая форма колебаний ротора при различных амплитудах

Роторы ГТД, делятся на жёсткие и гибкие. Ротор называется жестким, если его максимальная частота вращения 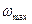меньше 0,5…0,7 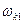. Если уравнение не выполняется, то ротор называется гибким. Преимуществом гибкого ротора, у которого 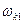< 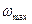, является то, что после прохождения критической частоты вращения он самоцентрируется. К его недостаткам относится то, что при запуске и остановке двигателя ротор проходит через резонанс. Чтобы при этом избежать разрушения ротора, обычно используются демпферы колебаний, которые будут рассмотрены далее.