Определение отношения удельных теплоёмкостей 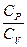 газов
газов
Основные представления из теории теплоёмкости.
При сообщении системе теплоты 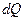 ее температура изменяется на dT. Величина
ее температура изменяется на dT. Величина
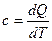 (1)
(1)
называется теплоемкостью и, по определению, есть отношение бесконечно малого количества поглощенной теплоты к бесконечно малому повышению температуры, вызванному этой теплотой.
Теплоемкость зависит от массы тела. Теплоемкость единицы массы вещества называют удельной теплоемкостью, а теплоемкость одного моля вещества- молярной теплоемкостью.
Между молярной С и удельной с теплоемкостями имеет место соотношение:
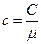 , (2)
, (2)
где μ - молярная масса.
B тех случаях, когда теплоемкость рассматривается как характеристика вещества, мы будем всегда подразумевать молярную теплоемкость С.
Если известна зависимость С(Т) теплоемкости от температуры, то можно найти малое количество теплоты 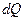 ,полученное системой в данном процессе при малом изменении температуры, а затем, с помощью интегрирования и количество теплоты Q, полученное системой при изменении температуры в пределах от
,полученное системой в данном процессе при малом изменении температуры, а затем, с помощью интегрирования и количество теплоты Q, полученное системой при изменении температуры в пределах от 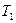 до
до 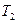 :
:
|
|
|
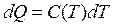 и
и 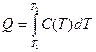 (3)
(3)
Теплоемкость зависит от условий, в которых телу сообщается теплота и изменяется его температура.
В самом деле, так как согласно первому началу термодинамики количество теплоты, полученное системой, зависит от вида процесса, который происходит с системой, то теплоемкость также должна зависеть от вида процесса. Так как различных процессов может быть бесконечно много, то существует и бесконечное количество теплоемкостей. При этом теплоемкость может изменяться от бесконечных отрицательных до бесконечных положительных значений. Из этого следует, что выражение (1) может быть равным любому значению. Для придания теплоемкости (1) определенного значения необходимо указать условия, при которых идет процесс. Эти условия обозначаются в виде индексов у величин, входящих в (1). В физике наиболее важную роль играют две теплоемкости: 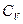 (при изохорическом процессе) и
(при изохорическом процессе) и 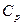 (при изобарическом процессе). Выделение теплоемкости
(при изобарическом процессе). Выделение теплоемкости 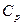 среди других теплоемкостей связано главным образом с тем, что чаще всего опыты производятся при постоянном атмосферном давлении. Из определения внутренней энергии следует, что она имеет вполне определенное значение в любом состоянии системы. Это означает, что внутренняя энергия U является функцией состояния, а dU - полным дифференциалом.
среди других теплоемкостей связано главным образом с тем, что чаще всего опыты производятся при постоянном атмосферном давлении. Из определения внутренней энергии следует, что она имеет вполне определенное значение в любом состоянии системы. Это означает, что внутренняя энергия U является функцией состояния, а dU - полным дифференциалом.
Величины P, V, T имеют вполне определенные значения в любом состоянии системы и характеризуют это состояние. Поэтому dP, dV, dT являются полными дифференциалами.
Теплоемкость при постоянном объеме.
Предположим, что нагревание тела происходит при постоянном объеме. Тогда молярная теплоемкость при изохорическом процессе определяется как
|
|
|
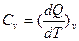 (4)
(4)
При постоянном объеме dV = 0 и, следовательно, уравнение первого закона термодинамики
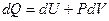 (5)
(5)
принимает вид 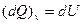
Это означает, что 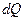 при
при 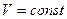 -полный дифференциал. Формула (4) принимает вид:
-полный дифференциал. Формула (4) принимает вид:
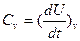 (6)
(6)
Отсюда видно, что 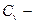 функция состояния, что обуславливает важное значение этой величины. В частности, из (6) следует, что при V=const
функция состояния, что обуславливает важное значение этой величины. В частности, из (6) следует, что при V=const
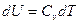 (7)
(7)
Внутренняя энергия идеального газа не зависит от объема или давления, а лишь функцией его температуры. Поэтому формула (7) в случае идеального газа справедлива для любого процесса.
Теплоемкость при постоянном давлении.
При P =const уравнение (5) может быть записано в виде
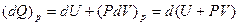 (8)
(8)
Это означает, что 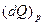 - полный дифференциал, а
- полный дифференциал, а
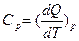 - функция состояния. (9)
- функция состояния. (9)
Входящая в (8) функция состояния
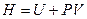 (10)
(10)
называется энтальпией. Поэтому выражение (9)можно записать в виде:
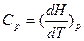 (11)
(11)
Соотношение между теплоемкостями.
Рассматриваемая нами термодинамическая система характеризуется тремя макроскопическими параметрами Р, V, Т. Эти параметры не независимы. Между ними существует соотношение, которое называется уравнением состояния. Для идеального газа уравнением состояния является уравнение Менделеева- Клапейрона:
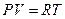 (12)
(12)
Для произвольного случая точный вид зависимости между этими величинами неизвестен. Поэтому можно записать лишь то, что эти величины находятся между собой в функциональных связях, например,
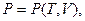
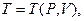
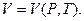 Все зависит от того, какие переменные выбираются за независимые. Если за независимые переменные выбраны V, Т, то внутренняя энергия системы зависит от них, то есть
Все зависит от того, какие переменные выбираются за независимые. Если за независимые переменные выбраны V, Т, то внутренняя энергия системы зависит от них, то есть 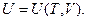 Подставляя выражение для полного дифференциала
Подставляя выражение для полного дифференциала
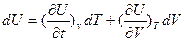 (13)
(13)
в (5), находим
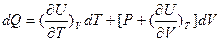 (14)
(14)
Тогда формула (1) для теплоемкости может быть записана в виде:
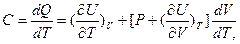 (15)
(15)
где 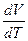 в правой части зависит от характера процесса. Для изохорического процесса (V=const) эта величина равна нулю и формула (15) превращается в (6) для
в правой части зависит от характера процесса. Для изохорического процесса (V=const) эта величина равна нулю и формула (15) превращается в (6) для 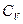 , так как при
, так как при 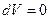
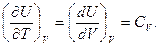
Если Р = const, то (15) превращается в выражение теплоемкости при постоянном давлении:
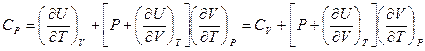 (16)
(16)
Следовательно, выражение (14) для dQ может быть представлено в виде
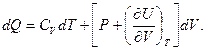 (17)
(17)
Соотношения между теплоемкостями идеального газа.
Одним из главных положений, лежащих в основе модели идеального газа, является возможность пренебрежения потенциальной энергии взаимодействия молекул. Поэтому внутренняя энергия идеального газа представляет собой только кинетическую энергию его молекул и, как следствие этого, она зависит только от температуры и не зависит от объема газа. Для идеального газа 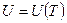 и
и 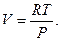 Поэтому
Поэтому
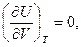
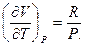 (18)
(18)
Подставляя (18) в (16), получим
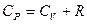 (19)
(19)
Полученное соотношение для теплоемкостей 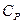 и
и 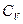 в идеальном газе называется уравнением Майера. Из уравнения (19) следует, что молярная газовая постоянная R численно равна работе, совершаемой одним молем идеального газа, расширяющимся при постоянном давлении при нагревании его на один кельвин.
в идеальном газе называется уравнением Майера. Из уравнения (19) следует, что молярная газовая постоянная R численно равна работе, совершаемой одним молем идеального газа, расширяющимся при постоянном давлении при нагревании его на один кельвин.
Теплоемкость идеального газа.
Термодинамика не позволяет построить теорию теплоемкости вещества. Приближенно теорию теплоемкости удалось создать исходя из молекулярно- кинетической теории, в которой движение молекул описывается законами классической механики Ньютона. В основе этой теории, получившей название классической, лежит закон равнораспредиления энергии по степеням свободы, согласно которому на каждую из степеней свободы частицы идеального газа приходится в среднем кинетическая энергия хаотического движения 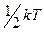 . Если частица идеального газа одноатомная, то она имеет три степени свободы поступательного движения. Ее энергия равна
. Если частица идеального газа одноатомная, то она имеет три степени свободы поступательного движения. Ее энергия равна 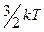 . Если же частица идеального газа сложная, то она обладает большим числом степеней свободы и, следовательно, большей энергией, Энергия сложной частицы слагается из кинетической энергии движения центра масс, кинетических энергии вращения и колебаний. В общем случае, если сложная частица имеет
. Если же частица идеального газа сложная, то она обладает большим числом степеней свободы и, следовательно, большей энергией, Энергия сложной частицы слагается из кинетической энергии движения центра масс, кинетических энергии вращения и колебаний. В общем случае, если сложная частица имеет 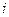 степеней свободы, то ее энергия равна
степеней свободы, то ее энергия равна 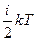 . В моле содержится
. В моле содержится 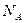 частиц (число Авогадро), и, следовательно, внутренняя энергия моля газа
частиц (число Авогадро), и, следовательно, внутренняя энергия моля газа
|
|
|
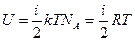 (20)
(20)
Тогда из формул (6) и (19) получаем
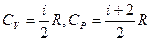 (21)
(21)
Во многие термодинамические соотношения входят не 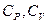 по отдельности, а отношение
по отдельности, а отношение
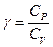 (22)
(22)
Величина 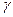 играет существенную роль при описании адиабатических процессов, поэтому ее часто называют адиабатической постоянной. Значение
играет существенную роль при описании адиабатических процессов, поэтому ее часто называют адиабатической постоянной. Значение 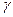 всегда больше единицы, так как
всегда больше единицы, так как 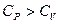 . Из формул (21)
. Из формул (21) 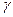 можно выразитьчерез число степеней свободы молекулы
можно выразитьчерез число степеней свободы молекулы
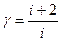 (23)
(23)
Так как 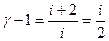 , то выражениеможно записать в виде
, то выражениеможно записать в виде
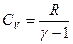 (24)
(24)
Итак согласно классической теории величины для данного газа являются константами - они не зависят от состояния газа, в частности, от его температуры, а зависят лишь от того, сколько степеней свободы имеют молекулы данного газа.
Для двухатомного газа с жесткой связью между атомами 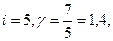 для многоатомного газа
для многоатомного газа 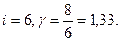
Вычисленные по приведенным выше формулам значения 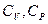 , а также их соотношение
, а также их соотношение 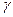 согласуются с экспериментальными значениями, полученными для одноатомных и двухатомных разреженных газов при температуре, близкой к комнатной.
согласуются с экспериментальными значениями, полученными для одноатомных и двухатомных разреженных газов при температуре, близкой к комнатной.
Однако, для некоторых двухатомных газов и для большинства многоатомных наблюдаются заметные расхождения с экспериментом. Лишь в небольшом числе случаев эти расхождения удается объяснить наличием колебательных степеней свободы. Расхождение теории с опытом особенно проявляется в обнаруженной на опыте зависимости теплоемкости газов от температуры (при изменении температуры в достаточно широких пределах), в то время как, согласно теории, такой зависимости вообще не должно быть.
Удовлетворительное объяснение всех опытных данных смогла дать только квантовая теория теплоемкости. По законам квантовой механики энергия вращательного и колебательного движений молекул изменяется лишь определенными порциями - квантами. При этом энергия вращательного и колебательного движений молекул зависит не только от температуры, но и от присущих им значений моментов инерции и частот колебаний. Энергия вращательного движения передается квантами, величина которых мала по сравнению со средней энергией, приходящейся на одну степень свободы движения молекул при комнатной температуре. Поэтому при такой температуре можно пренебречь квантовой природой энергии, связанной с вращением молекул, и пользоваться при расчете теплоемкостей классической теорией. Наоборот, кванты, которыми передается энергия колебательного движения молекул, примерно в 10 раз больше средней энергии, приходящейся на одну степень свободы движения молекул при комнатной температуре. Следовательно, при этой температуре колебательного движения молекул не возникает и при расчете теплоемкости газа можно не учитывать колебательные степени свободы.
|
|
|
Лишь у некоторых сложных молекул, из которых состоят пары различных органических соединений, квант энергии колебательного движения сопоставим со средней энергией, приходящейся на одну степень свободы движения молекул при комнатной температуре. Естественно, что в этом случае при вычислении теплоемкости нужно учитывать и степени свободы колебательного движения.
Адиабатический процесс. Уравнение Пуассона.
Говорят, что термодинамическая система совершает адиабатический процесс, если он обратим и если система термически изолирована, так что во время процесса не может происходить теплообмена между системой и окружающей ее средой. Так как процесс теплообмена требует некоторого времени, то адиабатическими приближенно можно считать такие процессы, происходящие достаточно быстро, то есть такие, при которых система не успевает вступить в теплообмен с окружающей средой. Примером этого могут служить процессы сжатия и расширения газа, обусловленные происхождением в нем звуковых волн.
Так при адиабатическом процессе 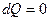 то уравнение первого закона термодинамики принимает вид
то уравнение первого закона термодинамики принимает вид
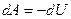 (25)
(25)
то есть, работа совершаемая системой при адиабатическом процессе, происходит за счет изменения ее внутренней энергии. Учитывая выражения 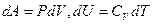 , уравнение (25) можно представить в виде
, уравнение (25) можно представить в виде
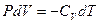 .
.
Используя уравнение состояния идеального газа 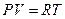 , можно исключить
, можно исключить 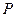 из приведенного выше уравнения и получить
из приведенного выше уравнения и получить
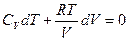 или
или 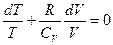
Интегрирование дает 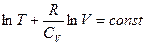
Потенцируя получаем 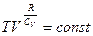
Учитывая, что 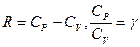 , после несложных преобразований находим
, после несложных преобразований находим 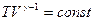 (26)
(26)
Это уравнение показывает нам количественно, как адиабатическое изменение объема идеального газа влияет на изменение его температуры. Воспользовавшись уравнением состояния идеального газа, можно в уравнение (26) заменить 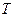 через
через 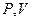 , и записать его в виде
, и записать его в виде
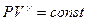 (27)
(27)
 Это уравнение адиабаты идеального газа в переменных получило название уравнения Пуассона.
Это уравнение адиабаты идеального газа в переменных получило название уравнения Пуассона.
Уравнение (27) следует сравнить с уравнением
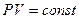 (28)
(28)
|
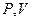 должен быть в
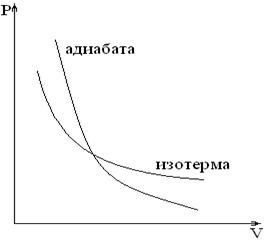
должен быть в 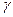 раз больше, чем у изотермы. Действительно,
раз больше, чем у изотермы. Действительно, 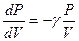 , в то время как по уравнению (28)
, в то время как по уравнению (28) 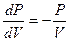 .
.
Следовательно, адиабата круче спадает к оси объемов, чем изотерма (рис.1) Объясняют это тем, что в отличии от изотермического процесса, адиабатическое изменение объема газа сопровождается при сжатии повышением температуры, а при расширении понижением. Отметим, что поскольку при адиабатическом процессе 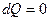 , то в соответствии с соотношением (1) теплоемкость при адиабатическом процессе постоянна и равна нулю.
, то в соответствии с соотношением (1) теплоемкость при адиабатическом процессе постоянна и равна нулю.
Политропический процесс.
Все рассмотренные раннее процессы обладают одной общей особенностью - они происходят при постоянной теплоемкости. Процесс, в котором теплоемкость является постоянной величиной,называется политропическим. Изобарический, изохорический, изотермический и адиабатический процессы являются частными случаями политропического процесса.
Уравнение политропы.
Из требования чтобы теплоемкость была постоянной в процессе, в частности, не зависела от 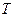 ,следует, что первое начало термодинамики должно иметь вид
,следует, что первое начало термодинамики должно иметь вид
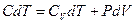 или
или 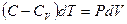 . (29)
. (29)
Из уравнения состояния 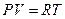 дифференцированием найдем выражение для
дифференцированием найдем выражение для 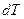
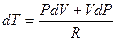
Подставив это выражение в (29) и заменив 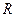 равным ему выражением
равным ему выражением 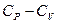 получим
получим 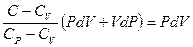
Отсюда легко получаем 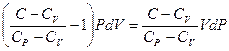
Разделив переменные и производя простые преобразования, найдем:
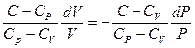
Отсюда, интегрируя это уравнение, находим:
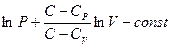 обозначим
обозначим 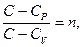 тогда
тогда
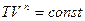 (30)
(30)
Показатель n - показатель политропы. Очевидно, что при 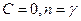 и из (30) получается уравнение адиабаты; при
и из (30) получается уравнение адиабаты; при 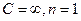 - уравнение изотермы; при
- уравнение изотермы; при 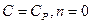 - уравнение изобары; при
- уравнение изобары; при 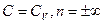 -уравнение изохоры.
-уравнение изохоры.
Определение отношения удельных теплоемкостей газов.
Как было сказано выше, величина отношения 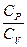 для газов играет большую роль при адиабатическом процессе и при процессах близких к ним. В частности, этой величиной определяется скорость распространения звука в газах, от нее зависит течение газов по трубам со звуковыми скоростями и достижение сверхзвуковых скоростей в расширяющихся трубах.
для газов играет большую роль при адиабатическом процессе и при процессах близких к ним. В частности, этой величиной определяется скорость распространения звука в газах, от нее зависит течение газов по трубам со звуковыми скоростями и достижение сверхзвуковых скоростей в расширяющихся трубах.
Принадлежности: баллон с распределительным краном, v образный манометр, насос.
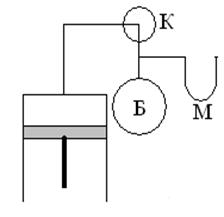
Описание установки.
Схема установки представлена на рис.1. Установка состоит из стеклянного баллона, который может быть соединен с помощью распределительного крана К либо с атмосферой, либо с насосом Н и манометром М, Водяной манометр измеряет разность между давлением в баллоне и атмосферным давлением в мм. вод. ст.
 Для определения отношения теплоемкостей
Для определения отношения теплоемкостей 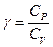 с газом, находящимся в баллоне, проводят последовательность термодинамических процессов.
с газом, находящимся в баллоне, проводят последовательность термодинамических процессов.
|
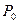 и температура
и температура 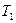 равная температуре окружающего воздуха. Если с помощью насоса накачать в баллон небольшое количество воздуха и закрыть кран, то давление в баллоне повысится, однако, если это повышение было произведено достаточно быстро, манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, температура его повысилась. Окончательная разность уровней в манометре устанавливается только тогда, когда температура воздуха внутри баллона сравняется благодаря теплообмену через стенки с температурой окружающего воздуха
равная температуре окружающего воздуха. Если с помощью насоса накачать в баллон небольшое количество воздуха и закрыть кран, то давление в баллоне повысится, однако, если это повышение было произведено достаточно быстро, манометрический столбик не сразу займет окончательное положение, так как сжатие воздуха было адиабатическим и, следовательно, температура его повысилась. Окончательная разность уровней в манометре устанавливается только тогда, когда температура воздуха внутри баллона сравняется благодаря теплообмену через стенки с температурой окружающего воздуха 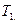 Обозначим через
Обозначим через 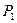 - давление газа внутри баллона, соответствующее показанию манометра
- давление газа внутри баллона, соответствующее показанию манометра 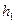 ясно, что
ясно, что
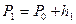 (31)
(31)
где - атмосферное давление.
Три параметра 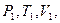 характеризуют состояние газа, которое мы назовем первым состоянием газа. Если теперь быстро открыть кран, то воздух в баллоне будет расширятся адиабатически, пока давление его не сделается равным
характеризуют состояние газа, которое мы назовем первым состоянием газа. Если теперь быстро открыть кран, то воздух в баллоне будет расширятся адиабатически, пока давление его не сделается равным 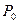 при этом он охладится до температуры
при этом он охладится до температуры 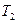 это будет вторым состоянием газа. Если сразу после открывания закрыть кран, то давление внутри баллона начнет возрастать вследствие того, что охладившийся при расширении воздух в баллоне станет снова нагреваться. Возрастание давления прекратится, когда температура воздуха в баллоне сравняется с внешней температурой это будет третьим состоянием газа. Обозначим давление воздуха в баллоне в этот момент через
это будет вторым состоянием газа. Если сразу после открывания закрыть кран, то давление внутри баллона начнет возрастать вследствие того, что охладившийся при расширении воздух в баллоне станет снова нагреваться. Возрастание давления прекратится, когда температура воздуха в баллоне сравняется с внешней температурой это будет третьим состоянием газа. Обозначим давление воздуха в баллоне в этот момент через 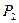 и соответствующее показание манометра - через
и соответствующее показание манометра - через 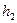 . Тогда
. Тогда
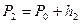 (32)
(32)
При адиабатическом расширении из сосуда выходит некоторая масса воздуха. Оставшаяся в сосуде масса воздуха в состоянии 1 имела объем 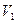 несколько меньший, чем объем сосуда. Дальнейшие расчеты проводятся для массы, оставшейся в сосуде. Переход от состояния 2 к состоянию 3 произошел без изменения объема. Поэтому мы вправе изменить закон Гей-Люсака
несколько меньший, чем объем сосуда. Дальнейшие расчеты проводятся для массы, оставшейся в сосуде. Переход от состояния 2 к состоянию 3 произошел без изменения объема. Поэтому мы вправе изменить закон Гей-Люсака
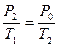 (33)
(33)
К процессу адиабатического расширения, то есть к переходу из состояния 1 в 2, может быть применен закон Пуассона, который удобно записать в форме 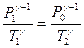
Подставляя сюда значение 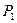 из уравнения (31) и переставляя члены, получим
из уравнения (31) и переставляя члены, получим
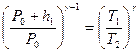 или
или 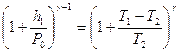
Так как 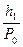 и
и 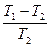 величины малые сравнительно с единицей, то, разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получим
величины малые сравнительно с единицей, то, разлагая оба двучлена по биному Ньютона и ограничиваясь членами первого порядка малости, получим 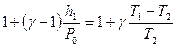 , откуда
, откуда 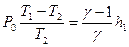 . Но выражение, стоящее в левой части уравнения, есть не что иное, как h2; действительно, подставив в уравнение (33) значение P2 из (32) и разрешив его относительно h2, получим
. Но выражение, стоящее в левой части уравнения, есть не что иное, как h2; действительно, подставив в уравнение (33) значение P2 из (32) и разрешив его относительно h2, получим
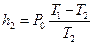
Следовательно, можно написать 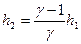 , откуда окончательно находим
, откуда окончательно находим 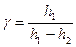 (34)
(34)
Измерения. Кран ставят так, чтобы полость насоса соединялась с баллоном Б. Действуя насосом осторожно, нагнетают воздух в сосуд. Когда разность уровней воды в манометре достигнет 8-10 см, кран поворачивают так, чтобы полость баллона полностью изолировалась от воздуха комнаты. После того, как давление установится, производят первый отсчет разности уровней в манометре 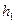 .
.
Поворотом крана устанавливают на один момент сообщение полости баллона с атмосферой так, чтобы давление в баллоне стало равным атмосферному. Затем кран вновь поворачивают, изолируя полость баллона, рекомендуется закрывать кран тотчас же после прекращения звука, создаваемого выходящим воздухом. После установления давления в сосуде производят второй отсчет разностей уровней в манометре 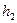 .
.
Опыт следует повторить не менее десяти раз, изменяя в каждом случае величину 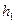 . Для каждой пары значений
. Для каждой пары значений 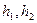 по формуле (34) определяют величину
по формуле (34) определяют величину 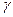 . За истинное значение принимают среднее арифметическое. По результатам измерений рассчитывают погрешность.
. За истинное значение принимают среднее арифметическое. По результатам измерений рассчитывают погрешность.
 2015-01-07
2015-01-07 2343
2343








